Closed form for $ \int_0^\infty {\frac{{{x^n}}}{{1 + {x^m}}}dx }$

Question

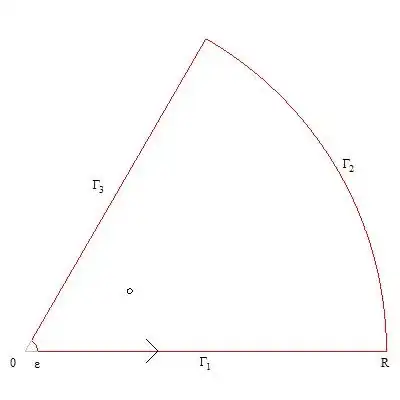
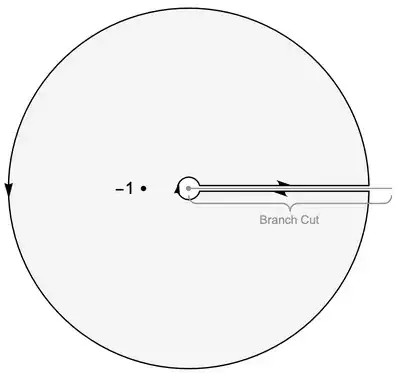
I've been looking at

$$\int\limits_0^\infty {\frac{{{x^n}}}{{1 + {x^m}}}dx }$$

It seems that it always evaluates in terms of $\sin X$ and $\pi$, where $X$ is to be determined. For example:

$$\displaystyle \int\limits_0^\infty {\frac{{{x^1}}}{{1 + {x^3}}}dx = } \frac{\pi }{3}\frac{1}{{\sin \frac{\pi }{3}}} = \frac{{2\pi }}{{3\sqrt 3 }}$$

$$\int\limits_0^\infty {\frac{{{x^1}}}{{1 + {x^4}}}dx = } \frac{\pi }{4}$$

$$\int\limits_0^\infty {\frac{{{x^2}}}{{1 + {x^5}}}dx = } \frac{\pi }{5}\frac{1}{{\sin \frac{{2\pi }}{5}}}$$

So I guess there must be a closed form - the use of $\Gamma(x)\Gamma(1-x)$ first comess to my mind because of the $\dfrac{{\pi x}}{{\sin \pi x}}$ appearing. Note that the arguments are always the ratio of the exponents, like $\dfrac{1}{4}$, $\dfrac{1}{3}$ and $\dfrac{2}{5}$. Is there any way of finding it? I'll work on it and update with any ideas.

---

UPDATE:

The integral reduces to finding

$$\int\limits_{ - \infty }^\infty {\frac{{{e^{a t}}}}{{{e^t} + 1}}dt} $$

With $a =\dfrac{n+1}{m}$ which converges only if

$$0 < a < 1$$

Using series I find the solution is

$$\sum\limits_{k = - \infty }^\infty {\frac{{{{\left( { - 1} \right)}^k}}}{{a + k}}} $$

Can this be put it terms of the Digamma Function or something of the sort?

Answer 1

I would like to make a supplementary calculation on BR's answer.

Let us first assume that $0 < \mu < \nu$ so that the integral $$ \int_{0}^{\infty} \frac{x^{\mu-1}}{1+x^{\nu}} \; dx $$ converges absolutely. By the substitution $x = \tan^{2/\nu} \theta$, we have $$ \frac{dx}{1+x^{\nu}} = \frac{2}{\nu} \tan^{(2/\nu)-1} \theta \; d\theta. $$ Thus $$ \begin{align*} \int_{0}^{\infty} \frac{x^{\mu-1}}{1+x^{\nu}} \; dx & = \int_{0}^{\frac{\pi}{2}} \frac{2}{\nu} \tan^{\frac{2\mu}{\nu}-1} \theta \; d\theta \\ & = \frac{1}{\nu} \beta \left( \frac{\mu}{\nu}, 1 - \frac{\mu}{\nu} \right) \\ & = \frac{1}{\nu} \Gamma \left( \frac{\mu}{\nu} \right) \Gamma \left( 1 - \frac{\mu}{\nu} \right) \\ & = \frac{\pi}{\nu} \csc \left( \frac{\pi \mu}{\nu} \right), \end{align*} $$ where the last equality follows from Euler reflexion formula.

Answer 2

The general formula (for $m > n+1$ and $n \ge 0$) is $\frac{\pi}{m} \csc\left(\frac{\pi (n+1)}{m}\right)$. IIRC the usual method involves a wedge-shaped contour of angle $2 \pi/m$.

EDIT: Consider $\oint_\Gamma f(z)\ dz$ where $f(z) = \frac{z^n}{1+z^m}$ (using the principal branch if $m$ or $n$ is a non-integer) and $\Gamma$ is the closed contour below:

$\Gamma_1$ goes to the right along the real axis from $\epsilon$ to $R$, so $\int_{\Gamma_1} f(z)\ dz = \int_\epsilon^R \frac{x^n\ dx}{1+x^m}$. $\Gamma_3$ comes in along the ray at angle $2 \pi/m$. Since $e^{(2 \pi i/m) m} = 1$, $\int_{\Gamma_3} f(z)\ dz = - e^{2 \pi i (n+1)/m} \int_{\Gamma_1} f(z)\ dz$. $\Gamma_2$ is a circular arc at distance $R$ from the origin. Since $m > n+1$, the integral over it goes to $0$ as $R \to \infty$. Similarly, the integral over the small circular arc at distance $\epsilon$ goes to $0$ as $\epsilon \to 0$. So we get

$$ \lim_{R \to \infty, \epsilon \to 0} \int_\Gamma f(z)\ dz = (1 - e^{2 \pi i (n+1)/m}) \int_0^\infty \frac{x^n\ dx}{1+x^m}$$

The meromorphic function $f(z)$ has one singularity inside $\Gamma$, a pole at $z = e^{\pi i/m}$ where the residue is $- e^{\pi i (n+1)/m}/m$. So the residue theorem gives you

$$ \int_0^\infty \frac{x^n\ dx}{1+x^m} = \frac{- 2 \pi i e^{\pi i (n+1)/m}}{ m (1 - e^{2 \pi i (n+1)/m})} = \frac{\pi}{m} \csc\left(\frac{\pi(n+1)}{m}\right)$$

Answer 3

Contour Integration Approach

Assuming only that $m>0$ and $-1<n<m-1$, let $z=x^m$ with the exaggerated contour $\gamma$:

$\gamma$ is actually tight above and below the positive real axis and around the origin and circles back at an arbitrarily large distance from the origin.

The part just above the positive real axis captures the integral. The part just below the positive real axis gets $-e^{2\pi i\frac{n-m+1}{m}}$ times the integral. The residue at $z=-1$ of $\frac{z^{\frac{n-m+1}{m}}}{1+z}$ is $e^{\pi i\frac{n-m+1}{m}}$. Putting this all together yields

$$ \frac1m\int_\gamma\frac{z^{\frac{n-m+1}{m}}}{1+z}\,\mathrm{d}z=\left(1-e^{2\pi i\frac{n-m+1}{m}}\right)\int_0^\infty\frac{x^n}{1+x^m}\,\mathrm{d}x $$ $$ \frac{2\pi i}{m}e^{\pi i\frac{n-m+1}{m}}=\left(1-e^{2\pi i\frac{n-m+1}{m}}\right)\int_0^\infty\frac{x^n}{1+x^m}\,\mathrm{d}x $$ $$ \frac{\pi}{m}=\sin\left(\pi\frac{n+1}{m}\right)\int_0^\infty\frac{x^n}{1+x^m}\,\mathrm{d}x $$ $$ \frac{\pi}{m}\csc\left(\pi\frac{n+1}{m}\right)=\int_0^\infty\frac{x^n}{1+x^m}\,\mathrm{d}x\tag1 $$

---

Relation to $\bf{\Gamma(\alpha)\Gamma(1-\alpha)}$

Setting $m=1$, $n=\alpha-1$, and using the substitution $s=tu$ yields Euler's Reflection Formula: $$ \begin{align} \Gamma(\alpha)\Gamma(1-\alpha) &=\int_0^\infty s^{\alpha-1}e^{-s}\,\mathrm{d}s\int_0^\infty t^{-\alpha}e^{-t}\,\mathrm{d}t\\ &=\int_0^\infty\int_0^\infty u^{\alpha-1}e^{-(tu+t)}\,\mathrm{d}u\,\mathrm{d}t\\ &=\int_0^\infty\frac{u^{\alpha-1}}{1+u}\,\mathrm{d}u\\[6pt] &=\pi\csc(\pi\alpha)\tag2 \end{align} $$

---

Another Proof of $\bf{(1)}$ $$ \begin{align} \int_0^\infty\frac{x^{\alpha-1}}{1+x}\,\mathrm{d}x &=\int_0^1\frac{x^{-\alpha}+x^{\alpha-1}}{1+x}\,\mathrm{d}x\\ &=\sum_{k=0}^\infty(-1)^k\int_0^1\left(x^{k-\alpha}+x^{k+\alpha-1}\right)\mathrm{d}x\\ &=\sum_{k=0}^\infty(-1)^k\left(\frac1{k-\alpha+1}+\frac1{k+\alpha}\right)\\ &=\sum_{k\in\mathbb{Z}}\frac{(-1)^k}{k+\alpha}\\[9pt] &=\pi\csc(\pi\alpha)\tag3 \end{align} $$ where the last step of $(3)$ is proven in $(3)$ of this answer. Then apply $(3)$ to get $$ \begin{align} \int_0^\infty\frac{x^n}{1+x^m}\,\mathrm{d}x &=\frac1m\int_0^\infty\frac{x^{\frac{n-m+1}m}}{1+x}\,\mathrm{d}x\\ &=\frac\pi{m}\csc\left(\pi\frac{n+1}m\right)\tag4 \end{align} $$

Answer 4

Use Ramanujan's Master theorem, with $u=x^b\Rightarrow dx=\frac{du}{bu^{1-\frac{1}{b}}}$:

$$\int_0^{\infty}\frac{x^{a-1}}{1+x^b}dx=\frac{1}{b}\int_0^{\infty}\frac{u^{\frac{a-1}{b}-1+\frac{1}{b}}}{1+u}du$$ $$=\frac{1}{b}\int_0^{\infty}u^{\frac{a}{b}-1}\sum_{k \ge 0}\frac{(-u)^k}{\Gamma(k+1)}\Gamma(k+1)du$$ $$=\frac{1}{b}\Gamma\left(\frac{a}{b}\right)\Gamma\left(1-\frac{a}{b}\right)=\frac{\pi}{b \sin \left(\frac{a\pi}{b}\right)}.$$

Answer 5

$\newcommand{\+}{^{\dagger}} \newcommand{\angles}[1]{\left\langle #1 \right\rangle} \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace} \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil #1 \right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\isdiv}{\,\left.\right\vert\,} \newcommand{\ket}[1]{\left\vert #1\right\rangle} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left( #1 \right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ With $\tt @Pedro Tamaroff$ identity $\ds{\sum_{k = - \infty }^\infty{\pars{-1}^{k} \over a + k}}$ we'll have:

\begin{align} &\sum_{k = - \infty }^\infty{\pars{-1}^{k} \over a + k} = {1 \over a} + \sum_{k = 1}^{\infty}\bracks{ {\pars{-1}^{-k} \over a - k} + {\pars{-1}^{k} \over a + k}} = {1 \over a} + \sum_{k = 1}^{\infty}\pars{-1}^{k + 1} {2a \over \pars{k - a}\pars{k + a}} \\[5mm]&= {1 \over a} + \sum_{k = 0}^{\infty}{2a \over \pars{2k + 1 - a}\pars{2k + 1 + a}} - \sum_{k = 0}^{\infty}{2a \over \pars{2k + 2 - a}\pars{2k + 2 + a}} \\[5mm] = &\ {1 \over a} + {a \over 2} \sum_{k = 0}^{\infty}{1 \over \pars{k + \pars{1 - a}/2}\pars{k + \pars{1 + a}/2}} \\[2mm] &\ - {a \over 2}\sum_{k = 0}^{\infty} {1 \over \pars{k + \pars{1 - a/2}}\pars{k + \pars{1 + a/2}}} \\[5mm] = &\ {1 \over a} + {a \over 2}\,{\Psi\pars{\bracks{1 - a}/2} - \Psi\pars{\bracks{1 + a}/2} \over \pars{1 - a}/2 - \pars{1 + a}/2} - {a \over 2}\,{\Psi\pars{1 - a/2} - \Psi\pars{1 + a/2} \over \pars{1 - a/2} - \pars{1 + a/2}} \\[5mm] = &\ {1 \over a} + \half\bracks{ -\Psi\pars{1 - a \over 2} + \Psi\pars{1 + a \over 2} + \Psi\pars{1 -{a \over 2}} -\Psi\pars{1 + {a \over 2}}} \end{align}

With the identities: $$ \Psi\pars{1 - z} = \Psi\pars{z} + \pi\cot\pars{\pi z}\,,\quad \Psi\pars{\half + z} = \Psi\pars{\half - z} + \pi\tan\pars{\pi z}\,,\quad \Psi\pars{1 + z} = \Psi\pars{z} + {1 \over z} $$ we'll get

\begin{align} &\color{#0000ff}{\large \sum_{k = - \infty }^\infty{\pars{-1}^{k} \over a + k}} = {1 \over a} + \half\bracks{ \pi\tan\pars{\pi a \over 2} + \Psi\pars{a \over 2} + \pi\cot\pars{\pi a \over 2} - \Psi\pars{a \over 2} - {2 \over a}} \\[3mm]&= {\pi \over 2}\,{\sec^{2}\pars{\pi a/2} \over \tan\pars{\pi a/2}} = {\pi \over \sin\pars{\pi a}} = \color{#0000ff}{\large\pi\,\csc\pars{\pi a}} \end{align}

Answer 6

This is in Gradshteyn/Ryzhik, formula 3.241.2: $$\int_0^\infty {x^{\mu-1}\over 1+x^\nu}\ dx={\pi\over\nu}\csc\bigg({\mu\pi\over\nu}\bigg)={1\over\nu}B\bigg({\mu\over\nu},{\nu-\mu\over\nu}\bigg)$$ assuming, of course, $Re(\nu)>Re(\mu)>0$, and where $B(x,y)$ denotes the Beta function $B(x,y)={\Gamma(x)\Gamma(y)\over\Gamma(x+y)}$.

---

To see the Beta function part of the equality, use the integral representation $$B(x,y)=\int_0^\infty {t^{x-1}\over (1+t)^{x+y}}\ dt$$ Then ${1\over\nu}B\big({\mu\over\nu},{\nu-\mu\over\nu}\big)$ is $${1\over\nu}\int_0^\infty {t^{{\mu\over\nu}-1}\over 1+t}\ dt$$ Send $t$ to $t^\nu$, and you are done!

Answer 7

The answers on both of these previous threads

Simpler way to compute a definite integral without resorting to partial fractions?

$\int_{0}^{\infty}\frac{dx}{1+x^n}$

provide a solution to exactly this problem.

Also this problem arise again in this newer thread:

Is there an elementary method for evaluating $\int_0^\infty \frac{dx}{x^s (x+1)}$?

The meta thread discussing the similarities between these 4 questions can be found here: http://meta.math.stackexchange.com/questions/3746/abstract-duplicates-what-to-do-in-this-scenario

Answer 8

$$t=\frac1{1+x^m}\qquad\iff\qquad x=\left(\frac1t-1\right)^\frac1m=\left(\frac{1-t}t\right)^\frac1m=t^{^{-\frac1m}}\cdot(1-t)^{^\frac1m}\qquad\iff$$

Can you already see where this is going ? ;-)

$$\iff\frac{dx}{dt}=\frac{d}{dt}\left[\left(\frac1t-1\right)^\frac1m\ \right]=\frac1m\left(\frac{1-t}t\right)^{\frac1m-1}\left(-\frac1{t^2}\right)=-\frac{t^{^{-\frac1m-1}}\cdot(1-t)^{^{\frac1m-1}}}m\iff$$

$$I=\int_0^\infty\frac{x^n}{1+x^m}dx=\frac1m\int_0^1t^{^{-\frac{n+1}m}}\cdot(1-t)^{^{\frac{n+1}m-1}}dt=\frac{B\left(1-\frac{n+1}m,\frac{n+1}m\right)}m$$

Now all we have to do is use the fact that $B(m,n)=\displaystyle\frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}$ , along with Euler's reflection formula, $\displaystyle\Gamma(z)\cdot\Gamma(1-z) = \frac{\pi}{\sin{(\pi z)}}$ , and we're done ! :-)

Answer 9

Letting $u =x^m$ entails $dx =\frac{1}{m}t^{1/m-1}$ and hence,

$$ \int\limits_0^\infty {\frac{{{x^n}}}{{1 + {x^m}}}dx } =\int\limits_0^\infty {\frac{t^{\frac{n+1}{m}-1}}{(1 + t)^{1}}dt } =\frac{1}{m}B\left(\frac{n+1}{m}, 1-\frac{n+1}{m}\right)\\=\color{red}{\frac{1}{m}\Gamma\left(\frac{n+1}{m}\right)\Gamma\left( 1-\frac{n+1}{m}\right)=\frac{\pi}{m\sin\left(\frac{\pi(n+1)}{m}\right)}}$$

where we made use of the beta and Gamma function and the Schwartz duplication formula

Answer 10

Integrate over a closed contour that is in the shape of a wedge in the 1st quadrant, having an angle of $\pi/5$. That is, consider

$$\oint_C dz \frac{z^2}{z^{10}+1}$$

where $C$ is that wedge contour. As mentioned above, the contour splits into 3 pieces:

$$\oint_C dz \frac{z^2}{z^{10}+1} = \int_0^R dx \frac{x^2}{x^{10}+1} + i R \int_0^{\pi/5}d\phi \, e^{i \phi} \frac{R^2 e^{i 2 \phi}}{R^{10} e^{i 10 \phi}+1}+ e^{i 3 \pi/5} \int_R^0 dx \frac{x^2}{x^{10}+1} $$

As $R \to \infty$, the second integral vanishes as $1/R^7$ (Note that the denominator never vanishes). The rest is then just equal to $i 2 \pi$ times the residue at the pole $z=e^{i \pi/10}$. Thus, combining the integrals, we have

$$\left (1-e^{i 3 \pi/5}\right) \int_0^{\infty} dx \frac{x^2}{x^{10}+1} = i 2 \pi \frac{e^{i 2 \pi/10}}{10 e^{i 9 \pi/10}} $$

Doing the algebra, I get

$$\int_0^{\infty} dx \frac{x^2}{x^{10}+1} = \frac{\pi}{10 \cos{(\pi/5)}}$$

Answer 11

Letting $\displaystyle \frac{1}{t}=x^{m}+1$, then $ \displaystyle d x=\frac{1}{m} \left(\frac{1}{t}-1\right)^{\frac{1}{m}-1}\left(-\frac{1}{t^{2}}\right) d t. $

Consequently $$ \begin{aligned} \int_{0}^{\infty} \frac{x^{r}}{x^{m}+1} d x &=-\int_{1}^{0} \frac{\left(\frac{1}{t}-1\right)^{\frac{r}{m}}}{\frac{1}{t}} \frac{1}{m t^{2}}\left(\frac{1}{t}-1\right)^{\frac{1}{m}-1} d t \\ &=\frac{1}{m} \int_{0}^{1} \frac{(1-t)^{\frac{r}{m}}(1-t)^{\frac{1}{m}-1}}{t^{\frac{r+1}{m}}} d t \\ &=\frac{1}{m} \int_{0}^{1} t^{-\frac{r+1}{m}}(1-t)^{\frac{r+1}{m}-1} d t \\ &=\frac{1}{m} B\left(1-\frac{r+1}{m}, \frac{r+1}{m}\right) \end{aligned} $$ By the property of Beta function,

$$ B(x, y)=\frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}, $$ where $\operatorname{Re}(x)>0$ and $\operatorname{Re}(y)>0,$

we have $$ \int_{0}^{\infty} \frac{x^{r}}{x^{m}+1} d x=\frac{\Gamma\left(1-\frac{r+1}{m}\right) \Gamma\left(\frac{r+1}{m}\right)}{m\Gamma(1)} $$

Using the Euler’s Reflection Theorem,

$$ \Gamma(1-z) \Gamma(z)=\pi \csc (\pi z), $$

where $z\notin Z$,

we can now conclude that $$\boxed{\int_{0}^{\infty} \frac{x^{r}}{x^{m}+1} d x=\frac{\pi}{m} \csc \frac{(r+1) \pi}{m}}$$