Evaluating $\int\limits_0^\infty \! \frac{x^{1/n}}{1+x^2} \ \mathrm{d}x$

Question

I've been trying to evaluate the following integral from the 2011 Harvard PhD Qualifying Exam. For all $n\in\mathbb{N}^+$ in general:

$$\int\limits_0^\infty \! \frac{x^{1/n}}{1+x^2} \ \mathrm{d}x$$

However, I'm not quite sure where to begin, even. There is a possibility that it is related to complex analysis, so I tried going at it with Cauchy's and also with residues, but I still haven't managed to get any further in solving it.

Answer 1

Beta function

I see @robjohn beat me to it. The substitution is slightly different, so here it is.

Here's a simple approach using the beta function.

First, notice the integral diverges logarithmically for $n=1$, since the integrand goes like $1/x$ for large $x$.

Let $t=x^2$. Then $$\begin{eqnarray*} \int_0^\infty dx\, \frac{x^{1/n}}{1+x^2} &=& \frac{1}{2}\int_0^\infty dt\, \frac{t^{(1-n)/(2n)}}{1+t} \\ &=& \frac{1}{2} \textstyle B\left(\frac{1}{2} + \frac{1}{2n}, \frac{1}{2} - \frac{1}{2n}\right) \\ &=& \frac{1}{2} \textstyle\Gamma\left(\frac{1}{2} + \frac{1}{2n}\right) \Gamma\left(\frac{1}{2} - \frac{1}{2n}\right) \\ &=& \frac{\pi}{2 \sin\left(\frac{\pi}{2} + \frac{\pi}{2n}\right)} \\ &=& \frac{\pi}{2} \sec \frac{\pi}{2n}. \end{eqnarray*}$$

Some details

Above we use the integral representation for the beta function $$B(x,y) = \int_0^\infty dt\, \frac{t^{x-1}}{(1+t)^{x+y}}$$ for $\mathrm{Re}(x)>0$, $\mathrm{Re}(y)>0$. We also use Euler's reflection formula, $$\Gamma(1-z)\Gamma(z) = \frac{\pi}{\sin\pi z}.$$

Addendum: A method with residue calculus

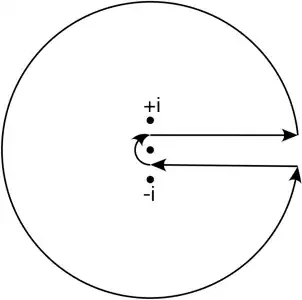
Let $t = x^{1/n}$. Then $$\begin{eqnarray*} I &=& \int_0^\infty dx\, \frac{x^{1/n}}{1+x^2} \\ &=& n\int_0^\infty dt\, \frac{t^n}{t^{2n}+1} \end{eqnarray*}$$ Notice the last integral has no cuts for integral $n$. The residues are at the roots of $t^{2n}+1=0$. Consider the pie-shaped contour with one edge along the positive real axis, another edge along the line $e^{i\pi/n}t$ with $t$ real and positive, and the "crust" at infinity.

$\hspace{4.5cm}$

There is one residue in the contour at $t_0 = e^{i\pi/(2n)}$. The integral along the real axis is just $I$. The integral along the other edge of the pie is $$\begin{eqnarray*} I' &=& n\int_\gamma dz\,\frac{z^n}{z^{2n}+1} \\ &=& n \int_\infty^0 dt e^{i\pi/n} \frac{t^n e^{i\pi}}{t^{2n}+1} \\ &=& -e^{i(n+1)\pi/n} I. \end{eqnarray*}$$ The integral along the crust goes like $1/R^{2n-1}$ as the radius of the pie goes to infinity, and so vanishes in the limit. Therefore, $$\begin{eqnarray*} I + I' &=& 2\pi i \,\mathrm{Res}_{t=t_0}\, \frac{t^n}{t^{2n}+1} \\ &=& 2\pi i \frac{t_0^n}{2n t_0^{2n-1}}. \end{eqnarray*}$$ Using this and the formula for $I'$ in terms of $I$ above we find $$I = \frac{\pi}{2} \sec \frac{\pi}{2n},$$ as before.

Answer 2

This is easily converted to a Beta integral. Let $x^2=\dfrac{t}{1-t}$, then $$ \begin{align} \int_0^\infty\frac{x^{1/n}}{1+x^2}\,\mathrm{d}x &=\frac12\int_0^1t^{\frac1{2n}-\frac12}(1-t)^{-\frac1{2n}-\frac12}\,\mathrm{d}t\tag{1}\\ &=\frac12\mathrm{B}\left(\frac1{2n}+\frac12,-\frac1{2n}+\frac12\right)\tag{2}\\ &=\frac12\Gamma\left(\frac1{2n}+\frac12\right)\Gamma\left(-\frac1{2n}+\frac12\right)\tag{3}\\ &=\frac\pi2\sec\left(\frac\pi{2n}\right)\tag{4} \end{align} $$

Explanation of steps:

1. substitute $x^2=\dfrac{t}{1-t}$

2. $\displaystyle\mathrm{B}(\alpha,\beta)=\int_0^1t^{\alpha-1}(1-t)^{\beta-1}\,\mathrm{d}t$

3. $\mathrm{B}(\alpha,\beta)=\dfrac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$

4. $\Gamma(\alpha)\Gamma(1-\alpha)=\dfrac{\pi}{\sin(\pi \alpha)}$

---

Another Contour Integration:

Let's consider the integral for arbitrary $\alpha\in(-1,1)$: $$ \int_0^\infty\frac{z^\alpha}{1+z^2}\,\mathrm{d}z $$ We will use the contour $\gamma$ shown exaggerated below. The path actually hugs the positive real axis on both sides, tightly circles the origin in a clockwise semicircle, and then circles the complex plane counter-clockwise at an arbitrarily large distance.

$\hspace{4.5cm}$

The integrals along the curves vanish as the semicircle gets smaller and the circle gets bigger. The integral just above the real axis is the integral we wish to compute and the integral just below the real axis is $-e^{2\pi i\alpha}$ times the integral we wish to compute ($\mathrm{d}z$ is reversed and $z^\alpha$ is multiplied by $e^{2\pi i\alpha}$).

$\gamma$ circles the singularities at $i$ and $-i$ in a counter-clockwise direction.

Therefore, $$ \begin{array}{lll} \color{#C00000}{2\pi i\,\mathrm{Res}_{z=i}\left(\frac{z^\alpha}{1+z^2}\right)} &\color{#00A000}{+2\pi i\,\mathrm{Res}_{z=-i}\left(\frac{z^\alpha}{1+z^2}\right)} &=\color{#0000FF}{(1-e^{2\pi i\alpha})}\int_0^\infty\frac{z^\alpha}{1+z^2}\,\mathrm{d}z\\ \color{#C00000}{\pi e^{\frac\pi2i\alpha}} &\color{#00A000}{-\pi e^{\frac{3\pi}{2}i\alpha}} &=\color{#0000FF}{(1-e^{2\pi i\alpha})}\int_0^\infty\frac{z^\alpha}{1+z^2}\,\mathrm{d}z\\ &\pi\sin\left({\frac\pi2\alpha}\right) &=\sin\left(\pi\alpha\right)\int_0^\infty\frac{z^\alpha}{1+z^2}\,\mathrm{d}z\\ &\frac\pi2\sec\left(\frac\pi2\alpha\right) &=\int_0^\infty\frac{z^\alpha}{1+z^2}\,\mathrm{d}z \end{array} $$ In particular, if we set $\alpha=\dfrac1n$, we get the same result as above.

Answer 3

This is not a complete solution, but just a remark that it is not necessary to appeal to non-elementary functions such as the $\Gamma$-function to do this integral, although this is certainly expedient!

Writing $x = u^n$, the integral becomes $$\int_{0}^{\infty} \dfrac{n u^n}{1 + u^{2n}} du.$$

Any integral of a rational function can be computed elementarily, via partial fractions. I'm not claiming that it's trivial in this case, but it is doable in principle, and surely in practice with a little patience.

Answer 4

This wikipedia link pointed out by others earlier is helpful(Example IV). In our case it is largely the same except there is a power of $1/n$ at the top instead of $1/2$. So using the same "keyhole" contour integral we can show the integral on the outer circle and inner circle vanishes, leaving only the part $$[\int^{R}_{\epsilon}+\int^{\epsilon}_{R}]f$$ to worry about. Since $f$ has a branch cut at $[0,\infty]$, the first integral becomes $$\int^{\epsilon}_{R}\frac{e^{|1/n\log[z]}e^{\frac{2\pi i}{n}}}{1+z^{2}}=\int^{\epsilon}_{R}\frac{z^{1/n}[\cos[\theta]+i\sin[\theta]]}{1+z^{2}}$$ Thus the whole integral when added up should be $$(1-e^{\frac{2\pi i}{n}})\int^{\infty}_{0}fdx$$

We now have $$\frac{z^{1/n}}{1+z^{2}}=\frac{1}{2i} \left( \frac{z^{1/n}}{z-i}-\frac{z^{1/n}}{z+i} \right)$$

Thus we only need to evaluate the residue at $i$ and $-i$. Taking the limit we have $$\lim_{z\rightarrow i}(z-i)\frac{z^{1/n}}{z-i}=i^{1/n}$$

Thus the difference is $$\frac{1}{2i}(i^{1/n}-(-i)^{1/n})=\frac{1}{2i} \left(\exp\left(\frac{\pi i}{2n}\right) - \exp\left({\frac{3/2 \pi i}{n}} \right) \right)$$

And the desired integral value is $$\frac{e^{\frac{\pi i}{2n}}-e^{\frac{3/2\pi i}{n}}}{2i\cdot(1-e^{\frac{2\pi i}{n}})}=\frac{1}{2i}\frac{x-x^{3}}{1-x^{4}}=\frac{x}{(1+x^{2})2i}=\frac{1}{2i\cdot(x^{4n-1}+x^{4n+1})}=\sec[{\frac{\pi}{2n}]}/4i,x=e^{\frac{\pi i}{2n}}$$ Mind that $x^{4n}=1$. Thus $x^{4n-1}+x$ should be real and equal to $2\cos[\frac{\pi}{2n}]$.

We now multiply the missing factor of $2\pi i$ in the residue theorem, we get:

$$\int^{\infty}_{0}fdx=\frac{\pi}{2}\sec[\frac{\pi}{n}]$$

Answer 5

See this question and this question which are strongly related, and deal with the general case of you integral, namely

$$B(m,n)=\int_0^\infty \frac{x^{m-1}}{1+x^n}dx=\frac{\pi}{n}\csc \frac{m\pi}{n}$$