How to compute: $\int\limits_0^{\infty} \frac{x^{1/3}}{1+x^{2}} dx$

Question

This question was asked in a masters of mathematics exam for which I am preparing.

Compute $\int\limits_0^{\infty} \frac{x^{1/3}}{1+x^{2}} dx$.

I could only think of substituting $y^3 = x$ and that does not change much.

Could somebody post a solution using residues or in ways besides here in this link?: How to compute the integral $\int_{0}^{\infty} \frac{x^{1/3}}{1+x^{2}} \ dx$

Edit : I am interested in the answers which use contour integration and residue calculus.

Answer 1

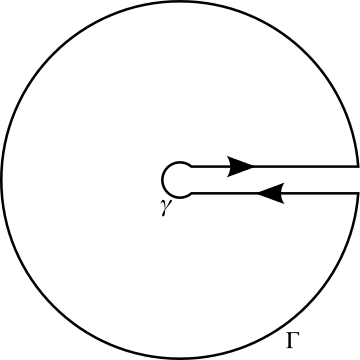
Evaluating $$\oint_C \frac{z^{\alpha-1}}{1+z} dz$$ we see that there is a branch cut along the positive $x-$axis and a pole at $z=-1$.

Take $C$ to be a keyhole contour consisting of a segment from $\epsilon$ to $R$, a circle of radius $R$, a segment from $R$ to $\epsilon$ and a small circle of radius $\epsilon$ surrounding the origin.

The result is:

$$\int_0^\infty \frac{ x^{\alpha-1}}{1+x} = \frac{\pi}{\sin \pi \alpha} \quad \text{when } 0<\alpha<1.$$

With the substitution $y^{1/2} = x$, our integral becomes

$$\bbox[5px, border: 1pt solid blue]{\int_0^\infty \frac{x^{1/3}}{1+x^2} dx = \frac{1}{2} \int_0^\infty \frac{y^{-1/3}}{1+y} dy = \frac{\pi}{2\sin \frac{2\pi}{3}}=\frac{\pi}{\sqrt{3}}.}$$

UPDATE:

In response to J.G.'s question:

The residue at $z=-1$ is $$b=\text{Res}_{z=-1} \frac{z^{\alpha-1}}{1+z}=e^{\pi i (\alpha-1)}.$$

So $$\oint_C \frac{z^{\alpha-1}}{1+z} dz = 2\pi i b$$

On the first segment (from $\epsilon$ to $R$), $z^{\alpha-1}=x^{\alpha-1}$, on the return trip, $z^{\alpha-1}=(e^{2\pi i} x)^{\alpha-1}.$

The integrals along the circles go to zero as $\epsilon\to0$, $R\to0$.

$$\int_0^\infty \frac{x^{\alpha-1}}{1+x}dx - \int_0^\infty \frac{e^{2\pi i (\alpha-1)} x^{\alpha-1}}{1+x}dx = 2\pi i e^{\pi i (\alpha-1)}$$

$$\begin{aligned} \int_0^\infty \frac{x^{\alpha-1}}{1+x}dx &=\frac{2\pi i e^{\pi i (\alpha-1)}}{1-e^{2\pi i (\alpha-1)}}\\ &= \frac{2\pi i}{e^{-\pi i (\alpha-1)}-e^{\pi i (\alpha-1)}} \\ &=\frac{\pi}{\sin \pi(1-\alpha)} \\ &= \frac{\pi}{\sin \pi \alpha}. \end{aligned}$$

Answer 2

With $x=\tan t$ it becomes $\int_0^{\pi/2}\tan^{1/3}tdt$. This can be evaluated in terms of the Beta function. In particualar, $\int_0^{\pi/2}\tan^{2s-1}tdt=\tfrac12\pi\csc\pi s$ implies your integral is $\tfrac12\pi\csc\frac{2\pi}{3}=\frac{\pi}{\sqrt{3}}$.

Answer 3

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ With Ramanujan's Master Theorem: \begin{align} \int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}\,\dd x & \,\,\,\stackrel{x^{2}\ \mapsto\ x}{=}\,\,\, {1 \over 2}\int_{0}^{\infty}{x^{\color{red}{2/3} - 1} \over 1 + x}\,\dd x \end{align} Note that $\ds{{1 \over 1 + x} = \sum_{k = 0}^{\infty}\pars{-1}^{k}x^{k} = \sum_{k = 0}^{\infty}\color{blue} {\Gamma\pars{k + 1}}{\pars{-x}^{k} \over k!}}$.

Then, \begin{align} \int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}\,\dd x & = {1 \over 2}\,\Gamma\pars{\color{red}{2 \over 3}} \color{blue} {\Gamma\pars{1 + \bracks{-\,\color{red}{2 \over 3}}}} \\[2mm] &= {1 \over 2}\,{\pi \over \sin\pars{\pi/3}} = \bbx{{\root{3} \over 3}\,\pi} \\ & \end{align}

Answer 4

First, let's do a substitution to reduce the number of poles to be computed. In this problem, it wouldn't be necessary, since the function is fairly easy and there aren't too many poles, however it's a good a practice since in the future you may encounter more intricated problems.

$$\int_{0}^{\infty}{\frac{x^\frac{1}{3}}{x^2+1}dx}=\frac{1}{2}\int_{0}^{\infty}{\frac{z^{-\frac{1}{3}}}{z+1}dz}$$

Now, let’s define our function and integration path. Bear in mind that since we are working with complex functions $z^{-\frac{1}{3}}=\exp{\left(-\frac{Log\left(z\right)}{3}\right)}$, wich means that we must take care of the branch point. Hence, the selection of the keyhole contour. $$f(z)=\frac{z^{-\frac{1}{3}}}{z+1}$$

$$\oint f(z)dz=\left(\int_{0+ir}^{R+ir}+\int_{\Gamma}+\int_{R-ir}^{0-ir}+\int_\gamma \right)f(z)dz$$

1)Let's start working with the two integrals in the positive axis of the Real Line: $$\displaystyle{\lim_{R\rightarrow \infty\\ r\rightarrow 0}}\left(\int_{0+ir}^{R+ir}\int_{R-ir}^{0-ir} \right)f(z)dz$$

Remember that: $$Log(z)=\log|z|+i\text{Arg}(z)$$

$$\int_0^\infty \frac{\exp\left(-\frac{\log\left(z\right)+0i}{3}\right)}{z+1}dz+\int_\infty^0 \frac{\exp\left(-\frac{\log\left(z\right)+2\pi i}{3}\right)}{z+1}dz=\left(1-e^{-\frac{2\pi i}{3}}\right)\int_0^\infty\frac{z^{-\frac{1}{3}}}{z+1}dz$$

2. To compute the others integrals let's make use of the the Estimation Lemma: $$\left\lvert\int_\Gamma f(z)dz\right\rvert\leq\displaystyle{\lim_{R\rightarrow \infty}}\left\lvert\int_0^{2\pi}\frac{\left(Re^{it}\right)^{-\frac{1}{3}}}{Re^{it}+1}Rie^{it}dt\right\rvert\leq\displaystyle{\lim_{R\rightarrow \infty}}2\pi R^{-\frac{1}{3}}\rightarrow 0$$

$$\left\lvert\int_\gamma f(z)dz\right\rvert\leq\displaystyle{\lim_{r\rightarrow 0}}\left\lvert\int_{2\pi}^{0}\frac{\left(re^{it}\right)^{-\frac{1}{3}}}{re^{it}+1}rie^{it}dt\right\rvert\leq\displaystyle{\lim_{r\rightarrow 0}}2\pi r^{\frac{2}{3}}\rightarrow 0$$

3. Finally, let's compute the residue: $$\oint f(z)dz=2\pi i\displaystyle{\lim_{z\rightarrow -1}}\frac{z^{-\frac{1}{3}}}{z+1}(z+1)=2\pi ie^{-\frac{\pi i}{3}}$$

Gathering all results: $$\int_0^\infty\frac{z^{-\frac{1}{3}}}{z+1}dz=\frac{2\pi ie^{-\frac{\pi i}{3}}}{1-e^{\frac{-2\pi i}{3}}}=\frac{\pi }{\frac{e^{\frac{\pi i}{3}}-e^{-\frac{\pi i}{3}}}{2i}}=\frac{\pi}{\sin\left(\frac{\pi}{3}\right)}=\frac{2\pi}{\sqrt{3}}$$

Hence: $$\boxed{\int_{0}^{\infty}{\frac{x^\frac{1}{3}}{x^2+1}dx}=\frac{\pi}{\sqrt{3}}}$$

Answer 5

Substitution $$x=y^{3/2}$$ allows to write $$I=\int\limits_0^\infty\dfrac{\sqrt[\large3]x\,\text dx}{1+x^2} = \dfrac32\int\limits_0^\infty\dfrac{y\,\text dy}{1+y^3}.$$ At the same time, substitution $$y=\dfrac1z$$ gives $$I= \dfrac32\int\limits_0^\infty\dfrac{\text dz}{1+z^3} = \dfrac32\int\limits_0^\infty\dfrac{\text dy}{1+y^3}.$$ Therefore, $$I= \dfrac34\int\limits_0^\infty\dfrac{(1+y)\,\text dy}{1+y^3} = \dfrac34\int\limits_0^\infty\dfrac{\text dy}{1-y+y^2} =3\int\limits_0^\infty\dfrac{\text dy}{3+(2y-1)^2}.\tag1$$ Integral $(1)$ does not require the residue approach: $$I=\dfrac{\sqrt3}2\arctan\dfrac{2y-1}{\sqrt3}\bigg|_0^\infty = \dfrac{\sqrt3}2\left(\dfrac\pi2+\dfrac\pi6\right),$$ $$\color{brown}{\mathbf{I=\dfrac\pi{\sqrt3}.}}$$