Use the Residue Theorem to evaluate the integral:

Question

$$\int_{0}^{∞} \frac{\sqrt{x}}{x^2+2x+5} dx$$

I'm thinking of using the "keyhole" contour, but I'm not sure how to proceed from there. Please help! Thanks!

Answer 1

Since the wikipedia page on methods of contour integration is flawed (check the talk section), consequently, most explanations concerning the calculus of integrals using a "keyhole contour" on the web are flawed or not rigorous enough, in my opinion.

I'll try to explain how to do this, or at least the part that is not well explained.

As mentioned above, you can avoid all these difficulties by substituting $x=u^2$ to get rid of the square root.

---

Let $r$,$R$ and $\alpha$ be three positive numbers, with $0<r<R$, and $0<\alpha<\pi$.

Let $U=\Bbb C\setminus \Bbb R_+$ the branch cut of $\Bbb C$ along the positive real axis.

Since $U$ is star-shaped with respect to any real negative number, it's a simply connected domain of $\Bbb C$.

Let $\gamma=\gamma_1+\gamma_2+\gamma_3+\gamma_4$ be the contour showned on the picture below (the red part is the branch cut) :

$\hspace{4cm}$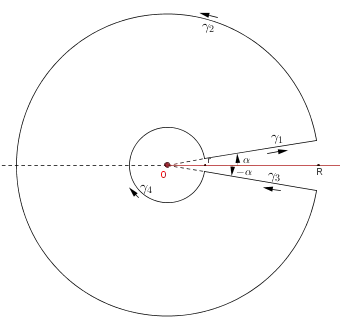

More precisely, we have :

$\hspace{5cm}\begin{array}{ccccl}\gamma_1&:&[r,R]&\longrightarrow& U\\ &&t&\longmapsto &te^{i\alpha}\end{array}$

$\hspace{5cm}\begin{array}{ccccl}\gamma_2&:&[\alpha,2\pi-\alpha]&\longrightarrow& U\\ &&t&\longmapsto &Re^{it}\end{array}$

$\hspace{5cm}\begin{array}{ccccl}\gamma_3&:&[-R,-r]&\longrightarrow& U\\ &&t&\longmapsto &-te^{-i\alpha}\end{array}$

$\hspace{5cm}\begin{array}{ccccl}\gamma_4&:&[\alpha,2\pi-\alpha]&\longrightarrow& U\\ &&t&\longmapsto &re^{-it}\end{array}$

We have $\mathrm{Supp}(\gamma)\subset U$, and we can define a holomorphic square root on $U$ like this :

$\hspace{1cm}$ If $z=re^{i\theta}$ with $r>0$ and $0<\theta<2\pi$, then $\sqrt{z}=\sqrt{r}e^{i\frac{\theta}2}$.

You can notice that the image of this function is the half open plane $\{z\in\Bbb C :\mathrm{Im}(z)>0\}$.

---

Now let : $\hspace{1cm} f:z\longmapsto \dfrac{\sqrt{z}}{z^2+2z+5}=\dfrac{\sqrt{z}}{g(z)}$

Since the function $g:z\longmapsto z^2+2z+5$ is a polynomial, it's holomorphic on $U$, and since it's non constant, the function $f$ is meromorphic on $U$ as a quotient of two holomorphic functions with a non constant zero denominator.

The zeros of $g$ are $z_\varepsilon=-1+2\varepsilon i$ with $\varepsilon=-1$ or $1$, and they are the poles of $f$. Since $\mid z_\varepsilon\mid=\sqrt 5$ and $\mathrm{Re}(z_\varepsilon)<0$, we will assume that $0<r<\sqrt 5<R$ and $0<\alpha<\dfrac{\pi}2$ from now on.

This way, the two poles of $f$ lie in the interior of $\gamma$, and the winding number around them with respect to $\gamma$ is 1.

By the residue theorem, we get :

$$\int_\gamma f(z)dz=2i\pi \sum_{\varepsilon\in\{-1;1\}} \mathrm{Res}(f,z_\varepsilon)$$

---

Let's calculate the residues of $f$ at $z_\varepsilon$, for $\varepsilon=-1$ and $1$.

They are simple poles of $f$, so : $$\mathrm{Res}(f,z_\varepsilon)=\lim_{z\to z_\varepsilon} (z-z_\varepsilon)\dfrac{\sqrt z}{g(z)}=\lim_{z\to z_\varepsilon} \left[\dfrac{z-z_{\varepsilon}}{g(z)-g(z_\varepsilon)}\times\sqrt{z}\right]=\dfrac{\sqrt{z_\varepsilon}}{g'(z_\varepsilon)}$$

We have $g'(z_\varepsilon)=2z_\varepsilon+2=2(z_\varepsilon+1)=4\varepsilon i$.

Letting $z_\varepsilon=(a+ib)^2$ with $(a,b)\in\Bbb R^2$ quickly leads to $\displaystyle\sqrt{z_\varepsilon}=\varepsilon\sqrt{\frac{\sqrt 5-1}2}+i\sqrt{\frac{\sqrt5+1}2}$ (remember that $\mathrm{Im}(\sqrt{z_\varepsilon})>0$)

So we get :

$$2i\pi\sum_{\varepsilon\in\{-1;1\}}\mathrm{Res}(f,z_\varepsilon)=\dfrac{2i\pi}{4i}(\sqrt{z_1}-\sqrt{z_{-1}})=\pi\sqrt{\frac{\sqrt 5 -1}2}$$

---

We found that : $$\int_\gamma f(z)dz=\sum_{k=1}^4 \int_{\gamma_k} f(z)dz=\pi\sqrt{\frac{\sqrt5-1}2}$$

No we will prove that these four integrals have a limit when $r$ and $R$ are fixed and $\alpha\longrightarrow 0$.

Of course, you can't just put $\alpha=0$ like this, because $f$ isn't defined on $\Bbb R_+$ !

• $\displaystyle\int_{\gamma_1} f(z)dz=\int_r^R f(\gamma_1(t))\gamma_1'(t)dt=\int_r^R \frac{\sqrt{t}e^{i\frac{3\alpha}2}}{g(te^{i\alpha})}dt$

The function $\displaystyle\left[0,\dfrac\pi 2\right]\times\left[r,R\right]\ni (\alpha,t)\mapsto \dfrac{\sqrt te^{i\frac{3\alpha}2}}{g(te^{i\alpha})}$ is continuous on a compact set so we can let $\alpha\rightarrow 0$ in the integrand (by dominated convergence) to get the limit $\displaystyle\int_r^R \dfrac{\sqrt{t}}{t^2+2t+5}dt$.

In the same manner, you can show that $\displaystyle\int_{\gamma_3} f(z)dz$ tends to the same limit.

• $\displaystyle\int_{\gamma_2} f(z)dz=\int_\alpha^{2\pi-\alpha} \frac{iR^{\frac32}e^{i\frac{3t}2}}{g(Re^{it})}dt=\int_0^{2\pi}\Bbb 1_{[\alpha,2\pi-\alpha]}(t) \frac{iR^{\frac32}e^{i\frac{3t}2}}{g(Re^{it})}dt$

Since $\displaystyle\left|1_{[\alpha,2\pi-\alpha]}(t) \frac{iR^{\frac32}e^{i\frac{3t}2}}{g(Re^{it})}\right|\leq \frac{R^{\frac{3}{2}}}{\mid g(Re^{it})\mid}\leq\frac1{\sqrt{R}}$ for all $(\alpha,t)\in\left[0,\dfrac{\pi}2\right]\times\left[0,2\pi\right]$, we find that $\displaystyle\int_{\gamma_2}f(z)dz$ tends to $\displaystyle\int_0^{2\pi}\frac{iR^{\frac 32}e^{i\frac{3t}2}}{g(Re^{it})}dt$ (again using dominated convergence) when $\alpha$ tends to $0$.

In the same manner, you can prove that $\displaystyle\int_{\gamma_4} f(z)dz$ tends to $\displaystyle\int_0^{2\pi}\frac{ir^{\frac32}e^{-i\frac{3t}2}}{g(re^{-it})}dt$

So we just proved that :

$$2\int_r^R \frac{\sqrt t}{t^2+2t+5}dt+\int_0^{2\pi}\frac{iR^{\frac 32}e^{i\frac{3t}2}}{g(Re^{it})}dt+\int_0^{2\pi}\frac{ir^{\frac32}e^{-i\frac{3t}2}}{g(re^{-it})}dt=\pi\sqrt{\frac{\sqrt 5 -1}2}$$

whenever $0<r<\sqrt 5<R$, so you can write, in such cases :

$$\int_r^R \frac{\sqrt t}{t^2+2t+5}dt=\frac{\pi}2\sqrt{\frac{\sqrt 5-1}2}-\frac 12\left(\int_0^{2\pi}\frac{iR^{\frac 32}e^{i\frac{3t}2}}{g(Re^{it})}dt+\int_0^{2\pi}\frac{ir^{\frac32}e^{-i\frac{3t}2}}{g(re^{-it})}dt\right)$$

Like the others before, I leave the rest to you : you have to prove that the limits of the two integrals in the parentheses are $0$ when $r$ tends to $0$ and $R$ tends to $+\infty$

Answer 2

The purpose of the keyhole contour is to exploit the multivalued-ness of the integrand to extract the integral value via residues. In this case, the keyhole contour is about the branch cut of the positive real axis, so that just above this cut the argument of $z$ is $0$, while below it is $2 \pi$.

We assume that the integral about the outer circular arc vanishes as the radius of that arc goes to $\infty$ (I leave proof to the reader), and that of the inner arc vanishes as the radius of that arc goes to zero (same).

Thus, the contour integral is

$$\begin{align}\oint_C dz \frac{\sqrt{z}}{z^2+2 z+5} &= \int_0^{\infty} dx \frac{\sqrt{x}}{x^2+2 x+5} - \int_0^{\infty} dx \frac{\sqrt{x e^{i 2 \pi}}}{x^2+2 x+5}\\ &= 2 \int_0^{\infty} dx \frac{\sqrt{x}}{x^2+2 x+5}\end{align}$$

where $C$ is the keyhole contour. As you can see, the multi-valuedness of the square root produces a factor of two in going up and back along the real axis in this fashion.

By the residue theorem, the contour integral is equal to $i 2 \pi$ times the sum of the residues of the poles inside the contour $C$. The poles are at $z_{\pm} = -1 \pm i 2i$. In polar form,

$$z_+ = \sqrt{5} e^{i(\pi-\arctan{2})}$$

$$z_- = \sqrt{5} e^{i (\pi + \arctan{2})}$$

Note that it is imperative that we get the arguments of the poles correct. These arguments must be between $0$ and $2 \pi$, because that is what we assumed in getting the above expression for the real integral. Getting the quadrant of the poles incorrect will lead to an incorrect result for the residues.

Since the poles are simple, we can use the following expression for the residues:

$$\text{Res}_{z=z_k} \frac{f(z)}{g(z)} = \frac{f(z_k)}{g'(z_k)}$$

The sum of the residues is then

$$\frac{5^{1/4} e^{i \pi/2 - i(\arctan{2})/2}}{i 4} + \frac{5^{1/4} e^{i \pi/2 + i(\arctan{2})/2}}{-i 4} = -i\frac{5^{1/4}}{2 \sqrt{2}} \sqrt{ 1-\frac{1}{\sqrt{5}}}$$

Therefore, taking into account the factor of $2$ next to the integral, we multiply this sum of the residues by $i \pi$ and the result is

$$\int_0^{\infty} dx \frac{\sqrt{x}}{x^2+2 x+5} = \frac{\pi}{2 \sqrt{2}} \sqrt{\sqrt{5}-1}$$

NB You can avoid using a keyhole contour by substituting $x=u^2$ and getting rid of the square root. In this case, you would use a semicircular contour in the upper half plane. Keep in mind, though, that the polynomial in the denominator is a quartic with four roots, two of which are within this new contour.

Answer 3

This type of integral has been worked out at here. The only difference is the evaluation of residue, which I assume you can work out yourself by checking the wikipedia article.