Help with integrating $\int_0^{\infty} \frac{(\log x)^2}{x^2 + 1} \operatorname d\!x$ - contour integration?

Question

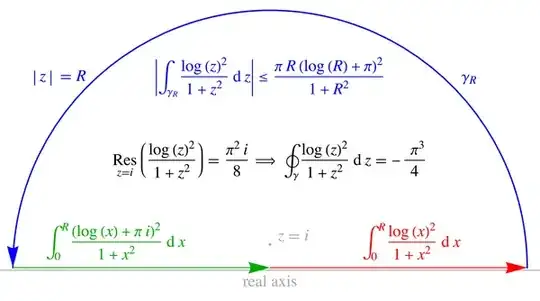
George Arfken's book: Mathematical Methods for Physicists has the following problem in a chapter on contour integration:

$\displaystyle \int_0^{\infty} \dfrac{(\log x)^2}{x^2 + 1} dx$.

Their suggestion is to make the substitution $x \rightarrow z=e^t$. I'm not sure what they meant by this, but I tried making the substitution $x = e^t$, which turns the integral into:

$\displaystyle\int_{-\infty}^{\infty} \dfrac{t^2 e^t}{1+e^{2t}} dt$.

The hint is then to take the contour from -R to R, to R+$\pi i$, to -R + $\pi i$, to -R. Since this has a pole at $t = \pi i/2$, a Laurent series expansion about this point gives the residue as $i \pi^2/8$, so the contour integral equals $-\pi^3/4$.

I've been able to show that the integral along R to R + $\pi i$ and along -R + $\pi i$ to -R goes to zero by the ML inequality - the denominator grows exponentially but the numerator quadratically.

But at this point, I'm a bit lost as to what to do with the integral over Im $t = \pi$. Any help? The book gives the answer as $\pi^3 /8$.

Answer 1

Fleshing out Ragib's idea: we have the substitution $\,t\to -u+\pi i\Longrightarrow dt=-du,$ , so we put

$$f(t):=\frac{t^2e^t}{1+e^{2t}}\Longrightarrow$$

$$\Longrightarrow\int_{R+\pi i}^{-R+\pi i}f(t)\,dt=-\int_{-R}^R\frac{(u^2-2\pi iu-\pi^2)e^{-u+\pi i}}{1+e^{-2u+2\pi i}}\,du=$$

$$=\int_{-R}^R\frac{u^2e^{-u}}{1+e^{-2u}}du-2\pi i\int_{-R}^R\frac{ue^{-u}}{1+e^{-2u}}\,du-\pi^2\int_{-R}^R\frac{e^{-u}}{1+e^{-2u}}\,du$$

The first integral above is just like the one on the real axis (BTW, note the signs in front of the two last integrals, which come from the factor $\,e^{\pi i}=-1\,$).

The last integral is

$$\pi^2\int_{-R}^R\frac{d(e^{-u})}{1+e^{-2u}}=\left.\pi^2\arctan e^{-u}\right|_{-R}^R=$$

$$=\pi^2\left(\arctan e^{-R}-\arctan e^R\right)\xrightarrow [R\to\infty]{}\pi^2\left(0-\frac{\pi}{2}\right)=-\frac{\pi^3}{2}$$

The second integral above is zero as the integrand is just $\,\frac{\pi iu}{\cosh u}\,$ , which is an odd function...

Denoting our integral by $\, I \,$, we thus have that

$$2I-\frac{\pi ^3}{2}=-\frac{\pi^3}{4}\Longrightarrow I=\frac{\pi^3}{8}$$

Answer 2

Consider the integral

$$\oint_\Gamma \frac{\log^3{z}}{1+z^2}dz$$

where $\Gamma$ is a ''keyhole'' contour in the complex plane, about the positive real axis. This contour integral may be seen to vanish along the outer and inner circular contours about the origin, so the contour integral reduces

$$\int_0^{\infty} \frac{\log^3{x}-(\log{x}+i 2 \pi)^3}{1+x^2} dx\\ = -i 6 \pi \int_0^{\infty} \frac{\log^2{x}}{1+x^2}dx +12 \pi^2 \int_0^{\infty} \frac{\log x}{1+x^2}dx +i8\pi^3\int_0^{+\infty}\frac{1}{1+x^2}dx. $$ The last integral is easy: $$ \int_{0}^{+\infty}\frac{1}{1+x^2}dx=\tan^{-1}x \Big|_{0}^{+\infty }=\frac{\pi}{2}. $$

By the residue theorem, the contour integral is also equal to $i 2 \pi$ times the sum of the residues at the poles $z_+=i=e^{i \pi/2}$, and $z_-=-i=e^{+i3\pi/2}$, where the branch cut of the logarithm has been conveniently placed along the positive real axis. In this case, with the simple poles, we have the simple formulas

$$ \text{Res}\frac{\log^3{z}}{1+z^2}\Big|_{z=z+}=\frac{\log^3{z}}{2z}\Big|_{z=z+}=-\frac{\pi^3}{16} $$ $$ \text{Res}\frac{\log^3{z}}{1+z^2}\Big|_{z=z-}=\frac{\log^3{z}}{2z}\Big|_{z=z-}=+\frac{27\pi^3}{16}. $$

Thus we have that

$$ i2\pi \left(\frac{27\pi^3}{16}-\frac{\pi^3}{16}\right) =-i 6 \pi \int_0^{\infty} \frac{\log^2{x}}{1+x^2}dx +12 \pi^2 \int_0^{\infty} \frac{\log x}{1+x^2}dx +i4\pi^3 $$ or $$ -i\frac{3}{4}\pi^4 = -i 6 \pi \int_0^{\infty} \frac{\log^2{x}}{1+x^2}dx +12 \pi^2 \int_0^{\infty} \frac{\log x}{1+x^2}dx. $$ Finally, equating real and imaginary parts: $$ \int_0^{+\infty}\frac{\log x}{1+x^2}dx=0 $$ $$ \int_0^{+\infty}\frac{\log^2{x}}{1+x^2}dx=\frac{\pi^3}{8}. $$

Answer 3

Using a semi-circular contour

and noting that $$ \int_0^\infty\frac{\log(x)}{1+x^2}\,\mathrm{d}x=0 $$ we get $$ \begin{align} -\frac{\pi^3}4 &=\oint_\gamma\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x\\ &=\int_0^\infty\frac{(\log(x)+\pi i)^2}{1+x^2}\,\mathrm{d}x+\int_0^\infty\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x\\ &=\int_0^\infty\frac{\log(x)^2-\pi^2}{1+x^2}\,\mathrm{d}x+\int_0^\infty\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x\\ &=2\int_0^\infty\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x-\frac{\pi^3}2\\ \end{align} $$ Therefore, $$ \int_0^\infty\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x=\frac{\pi^3}8 $$

Answer 4

If you simply write out the contour integral over Im $t=\pi$ as a real integral using the parametrization $t:[-R,R] \to \mathbb{C}: t\mapsto -t+i\pi$ then you see that the integral is something of the form $$ I + C_1 \int^{\infty}_{-\infty} \frac{t e^t}{1+e^{2t} } dt + C_2 \int^{\infty}_{-\infty} \frac{e^t}{1+e^{2t} } dt $$ where $I$ is the integral you want to find and $C_1, C_2$ are some known constants. The last integral is easily solved using an elementary substitution.

The middle one is solved by exactly the same procedure we've just applied in finding the original one: Set up the same contour, the sides go to 0, the part along Im $t=\pi$ is expressible in terms of the part along the real axis, and you can solve for it.