$$\int_0^\infty {(\ln x)^2 \over {1+x^2}} dx$$
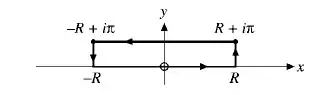
I need to evaluate the above integral using this specific rectangular contour to obtain the answer $\dfrac{\pi^3}8$:
However the only example involving rectangular contours I've seen in the textbook or in the many Youtube videos I've searched is the following:
$$\int_{-\infty}^{\infty} {{e^{ax} \over {1+e^x}}dx}$$
where $a$ is a constant between $0$ and $1$.
The hint is to use the substitution $x=e^t$ so I assume I'm suppose to turn the first integral into the form of the second, but then I end up with a $t^2$ I don't know what to do with. I am aware that if I solve the first integral from $-\infty$ to $\infty$ I just divide that answer by $2$ to get the answer from $0$ to $\infty$ so I guess the answer I'm really looking for is $\dfrac{\pi^3}4$.