I want to compute $$\int_{-\infty}^{\infty}{1 \over \cosh\left(\,x\,\right)}\, {\rm e}^{2\pi{\rm i}tx}\,{\rm d}x\,. $$
I tried contour integral ( real line and half circle ) to use residue theorem, but I think it does not vanish on the half circle.
I also just tried to find the answer in WolframAlpha but it didn't work.
How can I calculate this integral ?
$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\dsc}[1]{\displaystyle{\color{red}{#1}}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\Li}[1]{\,{\rm Li}_{#1}} \newcommand{\norm}[1]{\left\vert\left\vert\, #1\,\right\vert\right\vert} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ \begin{align}&\color{#66f}{\large% \int_{-\infty}^{\infty}{1 \over \cosh\pars{x}}\,\expo{2\pi\ic tx}\,\dd x} =2\overbrace{\int_{-\infty}^{\infty} {\pars{\expo{x}}^{2\pi\,\ic\,t} \over \pars{\expo{x}}^{2} + 1} \pars{\expo{x}\,\dd x}}^{\ds{\dsc{\expo{x}}\ \mapsto\ \dsc{x}}} =\dsc{2\int_{0}^{\infty}{x^{2\pi\,\ic\,t} \over x^{2} + 1}\,\dd x} \\[5mm]&=2\bracks{2\pi\ic\,{\pars{\expo{\ic\pi/2}}^{2\pi\,\ic\,t} \over 2\ic} +2\pi\ic\,{\pars{\expo{3\ic\pi/2}}^{2\pi\,\ic\,t} \over -2\ic} -\int_{\infty}^{0}{x^{2\pi\,\ic\,t}\pars{\expo{2\pi\ic}}^{2\pi\,\ic\,t} \over x^{2} + 1}\,\dd x} \\[5mm]&=2\pi\expo{-\pi^{2}\,t} - 2\pi\expo{-3\pi^{2}\,t} +\expo{-4\pi^{2}\,t}\ \dsc{2\int^{\infty}_{0}{x^{2\pi\,\ic\,t} \over x^{2} + 1}\,\dd x} \end{align} where we used a 'key-hole contour' as depicted in the following picture:
'
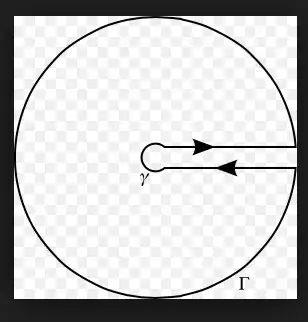Integrand poles are at $\dsc{\expo{\ic\pi/2} = \ic}$ and $\dsc{\expo{3\ic\pi/2} = -\ic}$ according to the $\ds{x^{2\pi\ic t}\,}$-branch cut.
Then,
\begin{align}&\color{#66f}{\large% \int_{-\infty}^{\infty}{1 \over \cosh\pars{x}}\,\expo{2\pi\ic tx}\,\dd x} =\dsc{2\int^{\infty}_{0}{x^{2\pi\,\ic\,t}\over x^{2} + 1}\,\dd x} =2\pi\,{\expo{-\pi^{2}\,t} - \expo{-3\pi^{2}\,t} \over 1 - \expo{-4\pi^{2}\,t}} \\[5mm]&=2\pi\,{\expo{\pi^{2}\,t} - \expo{-\pi^{2}\,t} \over \expo{\pi^{2}\,t} - \expo{-2\pi^{2}\,t}} =2\pi\,{\sinh\pars{\pi^{2}\,t} \over \sinh\pars{2\pi^{2}\,t}} ={\pi \over \cosh\pars{\pi^{2}\,t}} =\color{#66f}{\large\pi\sech\pars{\pi^{2} t}}\,,\qquad t \in {\mathbb R} \end{align}
The residue of $\dfrac{\color{#C00000}{e^{2\pi itz}}}{\color{#00A000}{\cosh(z)}}$ at $z=\left(n+\frac12\right)\pi i$ is $\color{#00A000}{(-1)^{n-1}i}\,\color{#C00000}{e^{-(2n+1)\pi^2t}}$, where $n\in\mathbb{Z}$.
Use the contour $$ \gamma=[-R,R]\,\cup\,\overbrace{R+iR[0,1]}^{|\mathrm{Re}(z)|=R}\,\cup\,\overbrace{[R,-R]+iR}^{|\mathrm{Im}(z)|=R}\,\cup\,\overbrace{-R+iR[1,0]}^{|\mathrm{Re}(z)|=R} $$ where $R=k\pi$ and $k\in\mathbb{Z}$. As $R\to\infty$, we get $$ \begin{align} \int_{-\infty}^\infty\frac{e^{2\pi itx}}{\cosh(x)}\mathrm{d}x &=\int_\gamma\frac{e^{2\pi itz}}{\cosh(z)}\mathrm{d}z\\ &=(2\pi i)\,i\sum_{n=0}^\infty(-1)^{n-1}e^{-(2n+1)\pi^2t}\\ &=\frac{2\pi e^{-\pi^2t}}{1+e^{-2\pi^2t}}\\[6pt] &=\frac{\pi}{\cosh(\pi^2t)} \end{align} $$
The integral along all contours but $[-R,R]$ vanish:
When $|\mathrm{Re}(z)|=k\pi$, $$ \left|\frac{e^{2\pi itz}}{\cosh(z)}\right|\le\frac{e^{-2\pi t\mathrm{Im}(z)}}{\sinh(k\pi)} $$ When $\mathrm{Im}(z)=k\pi$, $$ \left|\frac{e^{2\pi itz}}{\cosh(z)}\right|\le\frac{e^{-2\pi^2kt}}{\cosh(\mathrm{Re}(z))} $$
Try the rectangular contour $[-R, R] \cup \big(R + i [0, \pi] \big) \cup \big( i \pi + [-R, R] \big) \cup \big( -R + i [0,\pi] \big)$ (properly oriented to close the loop), and check that the contribution along the length-$\pi$ endpieces fall off to zero as $R \to \infty$.
Note that $\cosh (r + i \pi) = \cosh(r) \cosh(i \pi) + \sinh (r) \sinh (i \pi) = - \cosh(r)$, and so if $\hat f(t)$ denotes the desired Fourier transform, then it's not hard to see that $$ (1 + e^{-2 \pi^2 t}) \hat f(t) = 2 \pi i \operatorname{Res}_{x = \frac{i \pi}{2}} \frac{e^{2 \pi i x t}}{\cosh (x)} \, . $$
