Is there an elementary method for evaluating $\displaystyle \int_0^\infty \frac{dx}{x^s (x+1)}$?

Question

I found a way to evaluate $\displaystyle \int_0^\infty \frac{dx}{x^s (x+1)}$ using the assumption that $s\in\mathbb{R}$ and $0<s<1$.

Apparently it should be easily extended to all $s\in\mathbb{C}$ with $0<Re(s)<1$.

I posted my solution here: http://thetactician.net/Math/Analysis/Integral1.pdf

I'm pretty sure there's a more concise method for evaluating it...and I'd also like to make the extension to $\mathbb{C}$ more rigorous.

Any ideas?

Answer 1

Not elementary (in the sense of not using complex analysis), but this is how I'd do it:

Let $$f(z) = \frac{1}{z^s(z+1)},$$ where $z^s$ denotes the "natural branch", i.e. choose $\phi \arg z \in (0,2\pi)$ and put $(re^{i\phi})^s = r^s e^{is\phi}$. Take a "keyhole contour" C:

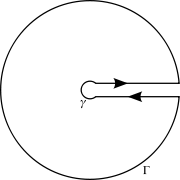
and integrate $f$ along $C$ using the residue theorem:

$$\int_C f(z)\,dz = 2\pi i \operatorname{Res}_{z=-1} f(z).$$

Estimating $\int_\gamma f(z)\,dz$ and $\int_\Gamma f(z)\,dz$, we have

$$\left| \int_\gamma f(z)\,dz \right| \le \frac{M}{r^{\mathrm{Re}(s)}} \cdot 2\pi r \to 0 \qquad\text{as }r\to0$$ and $$\left| \int_\Gamma f(z)\,dz \right| \le \frac{M}{R^{1+\mathrm{Re}(s)}} \cdot 2\pi R \to 0 \qquad\text{as }R\to\infty.$$

(For the first estimate, we want $\mathrm{Re}(s) < 1$ and for the second $\mathrm{Re}(s) > 0$.

For the two remaining line segments, on the "top" segment we get the integral we're looking for as $r \to 0$ and $R\to\infty$. On the "bottom" segment, we get (remember the choice of branch) $$-\int_0^\infty \frac{1}{x^s e^{2\pi i s} (1+x)}\,dx.$$

Putting it all together: $$(1-e^{-2\pi i s}) \int_0^\infty \frac{1}{x^s(1+x)}\,dx = 2\pi i \operatorname{Res}_{z=-1} f(z) = 2\pi i (-1)^{-s} = 2\pi i e^{-\pi i s}$$ so $$ \int_0^\infty \frac{1}{x^s(1+x)}\,dx = 2\pi i \frac{e^{-\pi i s}}{1-e^{-2\pi i s}} = \frac{\pi}{\sin s\pi}.$$

---

Answer 2

First, let $x=\frac{1}{t}$. Then our integral is $$\int_{0}^\infty \frac{t^{s-1}}{t+1}dt$$ which is the Mellin transform of the function $\frac{1}{1+t}$. In this math stack exchange answer it is shown that $$\mathcal{M}\left(\frac{1}{1+x^{b}}\right)(s)=\int_0^\infty \frac{t^{s-1}}{1+t^b}dt =\frac{\pi}{b}\csc\left(\frac{\pi s}{b}\right).$$

This solution uses the Beta function, and an identity relating it to the Gamma function which you may or may not consider to be elementary. (There are proofs of this identity which use no complex analysis)

In each of the following threads, there are answers which are of interest:

Simpler way to compute a definite integral without resorting to partial fractions?

$\int_{0}^{\infty}\frac{dx}{1+x^n}$

Closed form for $\int_0^\infty {\frac{{{x^n}}}{{1 + {x^m}}}dx }$

Answer 3

Letting $ y=\frac{1}{x+1}$ transforms the integral into a beta function. $$ \begin{aligned} I & =\int_1^0 \frac{y}{\left(\frac{1}{y}-1\right)^s} \cdot\left(\frac{d y}{-y^2}\right) \\ & =\int_0^1 y^{s-1}(1-y)^{-s} d y \\ & =B(s, 1-s) \\ & =\pi \csc (\pi s) \end{aligned} $$ where the last step comes from the reflection property of beta function.