8

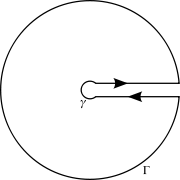
In complex analysis, we have general formula for $P(x)/Q(x)$ [$P$ and $Q$ are polynomials] from minus infinity to infinity, if $ \deg Q - \deg P > 2$.

Is it possible to have a general formula for improper integral of P(x)/Q(x) from 0 to infinity? Like,

$$\int_0^{\infty} \frac{1}{1+x^3} \mathrm{d} x =\frac{2\pi}{3\sqrt{3}} $$

$$\int_0^{\infty} \frac{1}{1+x+x^2+x^3} \mathrm{d} x =\frac{\pi}{4}$$

$$\int_0^{\infty} \frac{1}{(x+1)(x+2)(x+3)} \mathrm{d} x=\frac{\ln(4/3)}{2}$$

naslundx
  • 9,720
Kattern
  • 183
  • When you say 'we' do you mean you, your class or mathematics? I would like to see the integral formulas to speak of. – Ali Caglayan Apr 16 '14 at 08:39
  • @Alizter: He's probably referring to the straightforward application of the method of residues. – J. J. Apr 16 '14 at 08:46

1 Answers1

4

With residue calculus, put $$ f(z) = \frac{P(z)}{Q(z)}\log z$$ where $log$ denotes the natural branch, i.e. with a branch cut along the positive real axis. Integrate over a keyhole contour:

enter image description here

Assuming that $\deg Q \ge 2+ \deg P$ and that $Q$ has no zero on the positive real axis, it's not hard to show that the integral over the big and large circle vanish as $R \to \infty$ and $\varepsilon \to 0$. What remains is (after some cancellation along the positive real axis):

$$ -2\pi i \int_{0}^{\infty} \frac{P(x)}{Q(x)}\,dx = 2\pi i \sum \operatorname{Res} \Big( \frac{P(z)\log z}{Q(z)} \Big) $$ where the sum is taken over all poles of $P/Q$ (not just the ones in one half-plane). Remember to use the correct branch of $\log$ when you compute the residues.

Of course, if $P/Q$ happens to be even, you have a shorter solution.

Some concrete examples:

  1. Real integral by keyhole contour
  2. Is there an elementary method for evaluating $\int_0^\infty \frac{dx}{x^s (x+1)}$? (not a rational function, but same idea)
  3. Complex analysis and Residue theorem. (again not a rational function)
Community
  • 1
mrf
  • 43,639
  • (+1), I deleted my answer. – Zaid Alyafeai Apr 16 '14 at 09:49
  • I feel a little confused when I look the answer again. If the contour $r$ is around zero as in http://math.stackexchange.com/questions/114884, $\log z$ is approach to infinity when $r \to 0$. Is the contour a little different from that? – Kattern Apr 23 '14 at 12:07
  • @kattern $|\log z|$ does indeed tend to $\infty$ along the small circle, but the length of the small circle is $2\pi r$, and $2\pi r\max_{|z|=r} \log|z| \to 0$ as $r\to 0$. – mrf Apr 23 '14 at 12:24
  • @mrf Sorry, I thought $|\log z|$ approaches to $\infty$ faster than $r \to 0$. BTW, Why should $Q$ has no zero on positive real axis? Can Cauchy principal value be calculated in these cases? – Kattern Apr 23 '14 at 13:36
  • Can you explain in more detail the appearance of the factor $\log z$? I don't see why we cannot work directly with $P(z)/Q(z)$ instead. – Matemáticos Chibchas Apr 25 '23 at 16:38