Calculating the integral $\int_0^{\infty}{\frac{\ln x}{1+x^n}}$ using complex analysis

Question

I need to calculate $\int_0^{\infty}{\frac{\ln x}{1+x^n}}$ $,n\geq2$ using complex analysis. I probably need to use the Residue Theorem.

I use the function $f(z)={\frac{\ln z}{1+z^n}}$ in the normal branch.

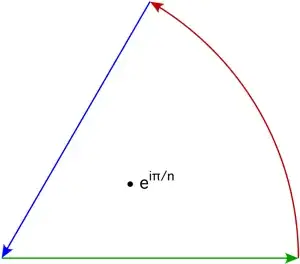
I've tried to use this contour.

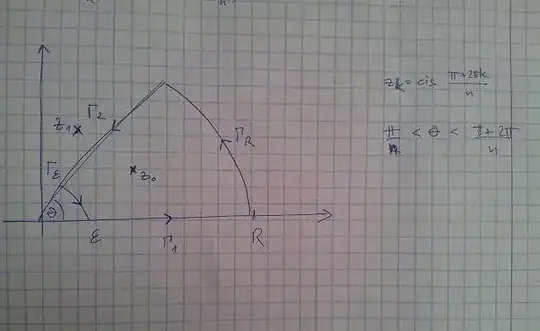
Where $\theta$ is an angle so that only $z_{0}$ will be in the domain (I hope this is clear from the drawing)

I estimated $|\int_{\Gamma_{R}}|$ and $|\int_{\Gamma_{\epsilon}}|$ and showed that they must tend to $0$ when $\epsilon \rightarrow0$ and $R \rightarrow\infty$. (Is it true?)

However I'm having trouble calculating $\int_{\Gamma_{2}}$ . Does it have something to do with choosing the "right" $\theta$?

Any ideas?

Thanks!

UPDATE

After Christopher's comment I chose $\theta=\frac{2\pi}{n}$ which gives, after the paramatrization $\Gamma (t) = te^{\frac{2\pi i}{n}}$, $t\in(\epsilon,R)$:

$$\int_{\Gamma_{2}}{\frac{\ln z}{1+z^n}dz} = \int_{\epsilon}^{R}{\frac{\ln (te^\frac{2\pi i}{n})}{1+t^n}e^\frac{2\pi i}{n}dt} = e^\frac{2\pi i}{n}\int_{\epsilon}^{R}{\frac{\ln t}{1+t^n}dt} + ie^\frac{2\pi i}{n}\int_{\epsilon}^{R}{\frac{\frac{2\pi}{n}}{1+t^n}dt} =$$ $$ = e^\frac{2\pi i}{n}\int_{0}^{\infty}{\frac{\ln t}{1+t^n}dt} + ie^\frac{2\pi i}{n}\int_{0}^{\infty}{\frac{\frac{2\pi}{n}}{1+t^n}dt} $$

But I have no idea how to deal with the second integral.

Answer 1

Using the contour in the question:

$\hspace{4cm}$

contour integration gives $$ \begin{align} &2\pi i\,\mathrm{Res}\left(\frac{\log(z)}{1+z^n},z=e^{i\pi/n}\right)\\ &=\frac{2\pi^2e^{i\pi/n}}{n^2}\\ &=\color{#00A000}{\lim_{R\to\infty}\int_0^R\frac{\log(x)}{1+x^n}\,\mathrm{d}x} \color{#C00000}{+\int_0^{2\pi/n}\frac{\log(R)+ix}{1+R^ne^{inx}}iRe^{ix}\mathrm{d}x} \color{#0000FF}{-e^{i2\pi/n}\int_0^R\frac{\log(x)+i2\pi/n}{1+x^n}\,\mathrm{d}x}\\ &=\left(1-e^{i2\pi/n}\right)\int_0^\infty\frac{\log(x)}{1+x^n}\,\mathrm{d}x -e^{i2\pi/n}\int_0^\infty\frac{i2\pi/n}{1+x^n}\,\mathrm{d}x\tag{1} \end{align} $$ where the green integral is the outgoing line, the red integral is the circular arc, and the blue integral is the returning line. For $n>1$, the integral in red vanishes as $R\to\infty$.

Dividing $(1)$ by $-2ie^{i\pi/n}$, we get $$ i\frac{\pi^2}{n^2}=\sin(\pi/n)\int_0^\infty\frac{\log(x)}{1+x^n}\,\mathrm{d}x +e^{i\pi/n}\int_0^\infty\frac{\pi/n}{1+x^n}\,\mathrm{d}x\tag{2} $$ Taking the imaginary part of $(2)$, we get $$ \frac{\pi^2}{n^2}=\sin(\pi/n)\int_0^\infty\frac{\pi/n}{1+x^n}\,\mathrm{d}x\tag{3} $$ and taking the real part of $(2)$, we get $$ \sin(\pi/n)\int_0^\infty\frac{\log(x)}{1+x^n}\,\mathrm{d}x +\cos(\pi/n)\int_0^\infty\frac{\pi/n}{1+x^n}\,\mathrm{d}x=0\tag{4} $$ Combining $(3)$ and $(4)$ yields $$ \int_0^\infty\frac{\log(x)}{1+x^n}\,\mathrm{d}x=-\frac{\pi^2}{n^2}\csc(\pi/n)\cot(\pi/n)\tag{5} $$

---

An alternate method

Using this result $$ \frac{\pi}{n}\csc\left(\pi\frac{m+1}{n}\right)=\int_0^\infty\frac{x^m}{1+x^n}\,\mathrm{d}x\tag{6} $$ Differentiating in $m$ yields $$ -\frac{\pi^2}{n^2}\csc\left(\pi\frac{m+1}{n}\right)\cot\left(\pi\frac{m+1}{n}\right)=\int_0^\infty\frac{\log(x)x^m}{1+x^n}\,\mathrm{d}x\tag{7} $$ Therefore, setting $m=0$ gives $$ -\frac{\pi^2}{n^2}\csc\left(\frac\pi n\right)\cot\left(\frac\pi n\right)=\int_0^\infty\frac{\log(x)}{1+x^n}\,\mathrm{d}x\tag{7} $$

Answer 2

Let us define, for $r>0$, $$\Gamma_{r}=\{r e^{i\alpha}\ :\ 0\leq\alpha\leq\theta\}$$ The circular arcs of your contour are then $\Gamma_{\epsilon}$ and $\Gamma_{R}$.

We note that, for $z\in\Gamma_{\epsilon}$ $$\left|\frac{\ln z}{1+z^n}\right|\leq|\ln z|\leq 2\ln\epsilon$$ if $\epsilon$ is small enough. So $$\left|\int_{\Gamma_\epsilon} f(z)\right|\leq 2\theta\epsilon\ln\epsilon$$ which goes to $0$ with $\epsilon$. Also, for $R$ large enough, $$|\ln z|\leq 2\ln R$$ when $z\in \Gamma_R$. So $$\left|\frac{\ln z}{1+z^n}\right|\leq\frac{2\ln R}{R^n-1}$$ hence $$\left|\int_{\Gamma_R} f(z)\right|\leq\theta R\frac{2\ln R}{R^n-1}$$ which goes to $0$ when $R\to\infty$, if $n>1$. (So, yes, these two pieces go to zero)

Now take $\Gamma_1=\{r\ :\ \epsilon\leq r\leq R\}$ and $\Gamma_2=e^{i\theta}\Gamma_1$; define the contour $\Gamma$ by walking along $\Gamma_1$, then $\Gamma_R$, then backwards along $\Gamma_2$ and $\Gamma_\epsilon$.

The roots of $1+z^n=0$ are the $n$-th roots of $-1$, that is $$z_k=e^{i\frac{(2k+1)\pi}{n}}$$ so, if we take $\theta\in (\frac{\pi}{n},\frac{3\pi}{n})$, $\Gamma$ surrounds exactly one pole of $f$.

Now, following the hint of Christopher A. Wong, we set $\theta=\frac{2\pi}{n}$; therefore, if $z\in\Gamma_2$, we get $z^n=|z|^ne^{in\theta}=|z|^n$ and $\ln z=\ln|z| + i\frac{2\pi}{n}$.

So $$\int_{\Gamma_2}f(z)=\int_{\epsilon}^R\frac{\ln x + i\frac{2\pi}{n}}{1+x^n}e^{i\frac{2\pi}{n}}dx$$

We recall that $$\int_0^\infty\frac{1}{1+x^n}dx=\frac{\pi/n}{\sin(\pi/n)}$$ with the same method we used now (integrating on $\Gamma$!).

Call $J=\int_{0}^\infty \ln x/(1+x^n) dx$ and $L$ the residue of $f(z)=\ln z /(1+z^n)$ at $z=e^{i\frac{\pi}{n}}$, then $$2i\pi L=J-e^{i\frac{2\pi}{n}}\left(J+i\frac{2\pi}{n}\frac{\pi/n}{\sin(\pi/n)}\right)$$ that is $$J=\frac{2i\pi L+ie^{i\frac{2\pi}{n}}\frac{2\pi^2/n^2}{\sin(\pi/n)}}{1-e^{i\frac{2\pi}{n}}}$$

Now it is enough to perform the computations.

Answer 3

Here's an alternative solution. Consider a standard keyhole contour:

and let $$f(z) = \frac{(\log z)^2}{1+z^n}$$ where $\log$ denotes the natural branch of the complex logarithm. The usual estimates over $\gamma$ and $\Gamma$ show that $$\int_\gamma f(z)\,dz \to 0 \qquad\text{and}\qquad \int_\Gamma f(z)\,dz \to 0$$ as $r \to 0$ and $R \to \infty$. In the limit, we will be left with $$\int_0^\infty \frac{(\ln x)^2}{1+x^n}\,dx$$ from the ''upper'' part of the real axis and $$-\int_0^\infty \frac{(\ln x + 2\pi i)^2}{1+x^n}\,dx$$ from the ''lower'' part. Adding these together, the $(\ln x)^2$-terms will cancel, and we end up with $$4\pi i \int_0^\infty \frac{\ln x}{1+x^n} - 4\pi^2 \int_0^\infty \frac{1}{1+x^n}\,dx.$$ By the residue theorem, this sum will be equal to $$2\pi i \sum \operatorname{Res}(f; \alpha_k)$$ where the sum is taken over all poles of $f$. These poles are given by the solutions to $z^n = -1$, i.e. $\alpha_k = \exp\Big( \frac{i\pi}{n}(2k+1) \Big)$ for $0 \le j \le n-1$. Also, \begin{align} \operatorname{Res}(f; \alpha_k) &= \frac{(\log \alpha_k)^2}{n\alpha_k^{n-1}} = -\frac{\alpha_k(\log \alpha_k)^2}{n} \\ &= -\frac{\exp\Big( \frac{i\pi}{n}(2k+1) \Big)\Big(\frac{i\pi}{n}(2k+1) \Big)^2}{n} \\ &= \frac{\pi^2}{n^3} \exp\Big( \frac{i\pi}{n}(2k+1) \Big)\Big((2k+1) \Big)^2. \end{align}

Summing up (while keeping track of all the $i$:s), we end up with \begin{align} \int_0^\infty \frac{\ln x}{1+x^n} &= -\frac12 \operatorname{Re} \left( \sum \operatorname{Res}(f; \alpha_k) \right) \\ &= -\frac{\pi^2}{2n^3} \sum_{j=0}^{n-1} \exp\Big( \frac{i\pi}{n}(2k+1) \Big)\Big((2k+1) \Big)^2. \end{align}

(I'll leave the algebra that shows that this answer is the same as the other one given as an exercise.)

Answer 4

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ $\ds{\int_{0}^{\infty}{\ln\pars{x} \over 1 + x^{n}}\,\dd x:\ {\large ?}.\qquad n \geq 2.}$

\begin{align} &\color{#c00000}{\int_{0}^{\infty}{\ln\pars{x} \over 1 + x^{n}}\,\dd x} =\int_{0}^{\infty}{\ln\pars{x^{1/n}} \over 1 + x}\,{1 \over n}\,x^{1/n - 1}\dd x ={1 \over n^{2}}\int_{0}^{\infty}{x^{1/n - 1}\ln\pars{x} \over 1 + x}\,\dd x \\[3mm]&={1 \over n^{2}}\lim_{\mu \to 1/n - 1}\partiald{}{\mu} \color{#00f}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x}\tag{1} \end{align}

\begin{align} &\color{#00f}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} =2\pi\ic\expo{\pi\mu\ic} -\int^{0}_{\infty}{x^{\mu}\expo{2\pi\mu\ic} \over 1 + x}\,\dd x =2\pi\ic\expo{\pi\mu\ic} +\expo{2\pi\mu\ic}\color{#00f}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} \end{align}

$$ \color{#00f}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} =2\pi\ic\expo{\pi\mu\ic}\,{1 \over 1 - \expo{2\pi\mu\ic}} =\pi\,{2\ic \over \expo{-\pi\mu\ic} - \expo{\pi\mu\ic}} =-\pi\csc\pars{\pi\mu} $$

Replacing in $\pars{1}$:

\begin{align} &\color{#66f}{\large\int_{0}^{\infty}{\ln\pars{x} \over 1 + x^{n}}\,\dd x} ={1 \over n^{2}} \lim_{\mu \to 1/n - 1}\partiald{\bracks{-\pi\csc\pars{\pi\mu}}}{\mu} \\[3mm]&={1 \over n^{2}}\, \lim_{\mu \to 1/n - 1}\bracks{\pi^{2}\cot\pars{\pi\mu}\csc\pars{\pi\mu}} ={\pi^{2} \over n^{2}}\,\cot\pars{{\pi \over n} - \pi} \csc\pars{{\pi \over n} - \pi} \\[3mm]&=\color{#66f}{\large-\,{\pi^{2} \over n^{2}}\,\cot\pars{{\pi \over n}} \csc\pars{{\pi \over n}}}\,,\qquad n > 1 \end{align}

Answer 5

For what is worth, one can exhibit the solution as $$\sum\limits_{k \in \Bbb Z} {{{{{\left( { - 1} \right)}^{k+1}}} \over {{{\left( {kn + 1} \right)}^2}}}} = \sum\limits_{ - \infty }^{ + \infty } {{{{{\left( { - 1} \right)}^{k+1}}} \over {{{\left( {kn + 1} \right)}^2}}}} $$

by making a change of varibles $x\mapsto e^u$ and then integrating over the positive and negative sides of $\Bbb R$ by expanding $$\frac 1{1+e^{nu}}$$ as $$\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {e^{nku}}$$ or $$\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {e^{-n(k+1)u}}$$ to assure convergence. Then one uses $$ - \int\limits_{ - \infty }^0 {u{e^{au}}du} = \int\limits_0^\infty {u{e^{ - au}}du} = {1 \over {{\alpha ^2}}}$$ to obtain a split series

$$\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {{ - 1} \over {{{\left( {nk + 1} \right)}^2}}} + \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {n\left( {k + 1} \right) - 1} \right)}^2}}}$$

which one can merge by $$\eqalign{ & \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {{ - 1} \over {{{\left( {nk + 1} \right)}^2}}} - \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^{k + 1}}} {1 \over {{{\left( {n\left( {k + 1} \right) - 1} \right)}^2}}} = \cr & - \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {nk + 1} \right)}^2}}} - \sum\limits_{k = 1}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {nk - 1} \right)}^2}}} = \cr & - \sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {nk + 1} \right)}^2}}} - \sum\limits_{k = 1}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( { - nk + 1} \right)}^2}}} = \cr & - \sum\limits_{ - \infty }^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {nk + 1} \right)}^2}}} = \cr & \sum\limits_{ - \infty }^\infty {{{\left( { - 1} \right)}^{k + 1}}} {1 \over {{{\left( {nk + 1} \right)}^2}}} \cr} $$

Most probably, one can confirm the series equals what robjohn wrote by using the identities relating polygamma-1 to the cotangent. In fact $$\int\limits_0^\infty {{{\log x} \over {1 + {x^n}}}dx} = 1 - {1 \over {{n^2}}}\left[ {\varphi \left( {{1 \over n}} \right) + \varphi \left( { - {1 \over n}} \right)} \right]$$ where $$\sum\limits_{k = 0}^\infty {{{\left( { - 1} \right)}^k}} {1 \over {{{\left( {k + z} \right)}^2}}} = \varphi \left( z \right)$$ if I'm not getting any sign wrong.

ADD Then, we have that $$I(n) = 1 - {1 \over {{n^2}}}\left[ {\varphi \left( {{1 \over n}} \right) + \varphi \left( { - {1 \over n}} \right)} \right] = 1 - {1 \over {{{\left( {2n} \right)}^2}}}\left[ {{\psi ^{\left( 1 \right)}}\left( {{1 \over {2n}}} \right) - {\psi ^{\left( 1 \right)}}\left( {{1 \over {2n}} + {1 \over 2}} \right) + {\psi ^{\left( 1 \right)}}\left( { - {1 \over {2n}}} \right) - {\psi ^{\left( 1 \right)}}\left( { - {1 \over {2n}} + {1 \over 2}} \right)} \right]$$

and W|A confirms that $$\psi^{(1)} \left( {{1 \over {2n}}} \right) - \psi^{(1)} \left( {{1 \over {2n}} + {1 \over 2}} \right) + \psi^{(1)} \left( { - {1 \over {2n}}} \right) - \psi^{(1)} \left( { - {1 \over {2n}} + {1 \over 2}} \right) ={4n}^2 + {\pi ^2}{\csc ^2}{\pi \over {2n}} - {\pi ^2}{\sec ^2}{\pi \over {2n}}$$ which proves what robjohn wrote, but I still can't find a source that proves this last identity.

Answer 6

This is NOT an answer to the original question. This is a justification of the final identity in Peter's answer. This was requested in chat, but too long to put there or in a comment box.

@Peter, all you need is recurrence and reflection for the trigamma function. Taking $z = 1/2n,$ first we find $$ \psi^{(1)} \left( 1 + \frac{1}{2n} \right) = \psi^{(1)} \left( \frac{1}{2n} \right) - \frac{1}{z^2} = \psi^{(1)} \left( \frac{1}{2n} \right) -4 n^2. $$ Next $$ \psi^{(1)} \left( 1 - \left( 1 + \frac{1}{2n} \right) \right) + \psi^{(1)} \left( 1 + \frac{1}{2n} \right) = \pi^2 \csc^2 \frac{\pi}{2n}, $$ so $$ \psi^{(1)} \left( - \frac{1}{2n} \right) + \psi^{(1)} \left( \frac{1}{2n} \right) - 4 n^2 = \pi^2 \csc^2 \frac{\pi}{2n}, $$ or $$ \psi^{(1)} \left( - \frac{1}{2n} \right) + \psi^{(1)} \left( \frac{1}{2n} \right) = 4 n^2 + \pi^2 \csc^2 \frac{\pi}{2n}. $$

Then $$ \psi^{(1)} \left( \frac{1}{2} - \frac{1}{2n} \right) + \psi^{(1)} \left( \frac{1}{2} + \frac{1}{2n} \right) = \pi^2 \csc^2 \left(\frac{\pi}{2} - \frac{\pi}{2n} \right) = \pi^2 \sec^2 \left( \frac{\pi}{2n} \right). $$

Answer 7

We can use Integration under Differentiation to solve this problem instead of residues or special functions. It is much easier. Let $$ J(a)=\int_0^\infty \frac{x^a}{1+x^n}dx. $$ Note $J'(0)=I$. First we calculate \begin{eqnarray} J(a)&=&\int_0^1\frac{x^a+x^{n-a-2}}{1+x^n}dx\\ &=&\int_0^1\sum_{k=0}^\infty(-1)^n(x^a+x^{n-a-2})x^{kn}dx\\ &=&\sum_{k=0}^\infty(-1)^k\left(\frac{1}{nk+a+1}+\frac{1}{nk+n-a-1}\right)\\ &=&\sum_{k=0}^\infty(-1)^k\frac{1}{nk+a+1}\\ &=&\sum_{k=-\infty}^\infty(-1)^k\frac{1}{nk+a+1}\\ &=&\frac{\pi}{n\sin(\frac{a+1}{n}\pi)}. \end{eqnarray} So $$ J'(0)=-\frac{\pi^2\cos(\frac{\pi}{n})}{n^2\sin^2(\frac{\pi}{n})}. $$ Here we used the following result $$ \sum_{k=-\infty}^\infty(-1)^k\frac{1}{ak+b}=\frac{\pi}{a\sin(\frac{b}{a}\pi)}.$$