Analytic integral of diverging function

Question

Is it possible to obtain the result of the following integral analytically?

$$\int_0^x \cfrac{{\rm d}u}{1-u^n}$$

I've tried using quadrature, but the function goes to infinity at $u=1$, hence the integral.

EDIT

I suppose an analytic solution is not possible, so is there any way to calculate it numerically for $u>1$? I managed to write:

from math import *
from scipy.integrate import quad
f = lambda u,n: 1./(1.-(u**n))
eps = 0.0001; n=2.6;
# from 0 to 1.005
print quad(lambda x:f(x,n),0.0,1.-eps)[0]+ quad(lambda x:f(x,n) ,1.+eps,1.005)[0]

I implemented the Cauchy principle value method in python 2.7 using scipy. Is there are particular reason for it not to work. For (u=1.005, n=2.6, x=u) the result should have been 2.022 (according to this (Open-Channel Flow by Subhash C. Jain, p78)). Instead, it is 2.48. Am I missing something? Can we say that $$\int_0^{x+\epsilon}\frac{\mathrm{d}u}{1-u^n} = \int_0^{x-\epsilon}\frac{\mathrm{d}u}{1-u^n}$$

Here are the numerical solutions that are supposedly correct:

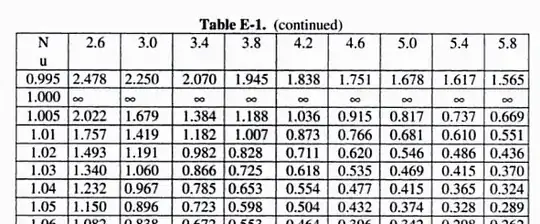
enter image description here

Solution:

Here is a snippet in python2.7 using the hyp2f1() function from the mpmath package

def F(u,n):
    if u < 1:
        return u*mpmath.hyp2f1(1/n,1,1/n+1,u**n)
    elif u >1:
        return (u**(1-n))/(n-1)* \
            mpmath.hyp2f1(1-1/n, 1 , 2-1/n ,u**(-1*n)) #+ pi/n/tan(pi/n)
    else:
        return 0.

You have a $u$ in the integrand and a $u$ as a limit of integration. Should the integration limit be $n$? — Antonio Vargas, Jan 06 '13 at 20:18
@AntonioVargas No, it is $u$. The function is used as the "varied flow function" in hydraulics. — osolmaz, Jan 06 '13 at 20:20
@nrs Do you want $$\int_0^x \dfrac{du}{1-u^n}?$$ It is preferred to use different variables for the integrand and the limits to avoid possible confusion. — , Jan 06 '13 at 20:20
Also, look at here: http://www.wolframalpha.com/input/?i=1%2F%281-u^n%29 . I've tried implementing the hypergeometric function, but I failed. — osolmaz, Jan 06 '13 at 20:22
@nrs For me all the $u$'s appear the same. Kindly change the variable name. — , Jan 06 '13 at 20:26
@nrs Thanks. Is $x < 1$?. Else the integral will not converge. — , Jan 06 '13 at 20:32
I think you should say the function goes to infnity at $1$, not that it "goes to infinity at $u$." — Michael Hardy, Jan 06 '13 at 20:49
nrs, could you take a screenshot of the page(s) from that book? I can't view them. — Antonio Vargas, Jan 07 '13 at 00:28
@nrs: for any $x\ne1$, we have that $$ \lim_{\epsilon\to0}\int_0^{x+\epsilon}\frac{\mathrm{d}u}{1-u^n} = \lim_{\epsilon\to0}\int_0^{x-\epsilon}\frac{\mathrm{d}u}{1-u^n} $$ However, the Cauchy Principal Value assumes that $$ \begin{align} &\lim_{\epsilon\to0}\left(\int_0^{1+\epsilon}\frac{\mathrm{d}u}{1-u^n} - \int_0^{1-\epsilon}\frac{\mathrm{d}u}{1-u^n}\right)\ &=\lim_{\epsilon\to0}\int_{1-\epsilon}^{1+\epsilon}\frac{\mathrm{d}u}{1-u^n}\ &=0 \end{align} $$ — robjohn, Jan 07 '13 at 00:56

score 4 · Answer 1 · edited Apr 13 '17 at 12:21

The integral can be given a value for $x\gt1$ using the Cauchy Principal Value. That is, for $x\gt1$, $$ \mathrm{PV}\int_0^x\frac{\mathrm{d}u}{1-u^n} =\lim_{\epsilon\to0}\left(\int_0^{1-\epsilon}\frac{\mathrm{d}u}{1-u^n} +\int_{1+\epsilon}^x\frac{\mathrm{d}u}{1-u^n}\right) $$

Cauchy Principal Value over $\mathbf{\mathbb{R}^+}$

Consider the contour

$\hspace{3cm}$ enter image description here

Using this answer, we get $$ \int_0^\infty\frac{\mathrm{d}u}{1+u^n}=\frac\pi n\csc\left(\frac\pi n\right) $$ Thus, the integral on the blue line is $$ -e^{i\pi/n}\frac\pi n\csc\left(\frac\pi n\right)=-\frac\pi n\cot\left(\frac\pi n\right)-i\frac\pi n $$ The residue of $\frac1{1-u^n}$ at $u=1$ is $-\frac1n$. Therefore, the integral along the clockwise red semicircle is $$ i\frac\pi n $$ Since there are no singularities inside the contour, the total integral over the contour is $0$. Thus, the integral over the perforated green line must be $$ \mathrm{PV}\int_0^\infty\frac{\mathrm{d}u}{1-u^n}=\frac\pi n\cot\left(\frac\pi n\right) $$

Self-Contained Argument

Using the contour above and separating real and imaginary parts, we get that $$ \begin{align} \color{#00A000}{\mathrm{PV}\int_0^\infty\frac{\mathrm{d}u}{1-u^n}}+\color{#C00000}{i\frac\pi n} &=\color{#0000FF}{e^{i\pi/n}\int_0^\infty\frac{\mathrm{d}u}{1+u^n}}\\ &=\left(\cos\left(\frac\pi n\right)+i\sin\left(\frac\pi n\right)\right)\int_0^\infty\frac{\mathrm{d}u}{1+u^n} \end{align} $$ Looking at the imaginary part, we get $$ \int_0^\infty\frac{\mathrm{d}u}{1+u^n}=\frac\pi n\csc\left(\frac\pi n\right) $$ Then looking at the real part, we get $$ \mathrm{PV}\int_0^\infty\frac{\mathrm{d}u}{1-u^n}=\frac\pi n\cot\left(\frac\pi n\right) $$

Can we say that $\int_0^{x+\epsilon}\frac{\mathrm{d}u}{1-u^n} = \int_0^{x-\epsilon}\frac{\mathrm{d}u}{1-u^n}$ — osolmaz, Jan 06 '13 at 23:49
@robjohn I also edited the question with some code to clarify my problem. — osolmaz, Jan 06 '13 at 23:54
@nrs: Cauchy Principal Value essentially assumes that $$ \lim_{\epsilon\to0}\int_{1-\epsilon}^{1+\epsilon}\frac{\mathrm{d}u}{1-u^n}=0 $$ — robjohn, Jan 07 '13 at 00:43

score 3 · Accepted Answer · edited Apr 13 '17 at 12:21

I can at least give your integral a name. Suppose $0 \leq x<1$ so that the integral converges.

Letting $u = v^{1/n}$, the integral becomes

$$ \frac{1}{n} \int_0^{x^n} v^{\frac{1}{n}-1}(1-v)^{-1}\,dv = \frac{1}{n}B\left(x^n;\,\frac{1}{n},\,0\right), $$

where $B(z;p,q)$ is the incomplete beta function. According to MathWorld, we can also write this as a hypergeometric function:

$$ x\cdot{}_2F_1\left(\frac{1}{n},\,1;\,\frac{1}{n}+1;\,x^n\right). $$

It appears (based on numerical evidence) that the principal value of the integrand is given by

$$ \text{PV} \int_0^x \frac{du}{1-u^n} = \operatorname{Re}\left[x\cdot{}_2F_1\left(\frac{1}{n},\,1;\,\frac{1}{n}+1;\,x^n\right)\right]. $$

This is in regards to the table posted in the question. They are not using the principal value of the integral; they are using a related quantity which differs from the principal value by a function depending only on $n$.

Let $0 < \epsilon < \min\{1,x-1\}$ and split the integral up into two parts,

$$ \begin{align*} &\int_0^{1-\epsilon} \frac{du}{1-u^n} + \int_{1+\epsilon}^{x} \frac{du}{1-u^n} \\ &\qquad = (1-\epsilon)\cdot{}_2F_1\left(\frac{1}{n},\,1;\,\frac{1}{n}+1;\,(1-\epsilon)^n\right) + \int_{1+\epsilon}^{x} \frac{du}{1-u^n}. \end{align*} $$

Making the substitution $u=1/v$ in the remaining integral gives

$$ \begin{align*} \int_{1+\epsilon}^{x} \frac{du}{1-u^n} &= -\int_{1/x}^{1/(1+\epsilon)}\frac{v^{n-2}}{1-v^n}\,dv \\ &= \int_0^{1/x}\frac{v^{n-2}}{1-v^n}\,dv - \int_0^{1/(1+\epsilon)}\frac{v^{n-2}}{1-v^n}\,dv. \end{align*} $$

Both of these integrals are treated the same way. We proceed as before, letting $v=w^{1/n}$. This gives

$$ \begin{align*} \int_0^a \frac{v^{n-2}}{1-v^n}\,dv &= \frac{1}{n} \int_0^{a^n} w^{\frac{n-1}{n}-1} (1-w)^{-1}\,dw \\ &= \frac{a^{n-1}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,a^n\right), \end{align*} $$

so that

$$ \begin{align*} \int_{1+\epsilon}^{x} \frac{du}{1-u^n} &= \frac{x^{1-n}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,x^{-n}\right) \\ &\qquad - \frac{(1+\epsilon)^{1-n}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,(1+\epsilon)^{-n}\right). \end{align*} $$

Thus

$$ \text{PV} \int_0^x \frac{du}{1-u^n} = \frac{x^{1-n}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,x^{-n}\right) + f(n), \tag{1} $$

where

$$ \begin{align*} f(n) &= \lim_{\epsilon \to 0} \left\{(1-\epsilon)\cdot{}_2F_1\left(\frac{1}{n},\,1;\,\frac{1}{n}+1;\,(1-\epsilon)^n\right) \right. \\ &\qquad\qquad\qquad \left. - \frac{(1+\epsilon)^{1-n}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,(1+\epsilon)^{-n}\right)\right\} \\ &= \frac{\pi}{n} \cot\left(\frac{\pi}{n}\right) \tag{2} \end{align*} $$

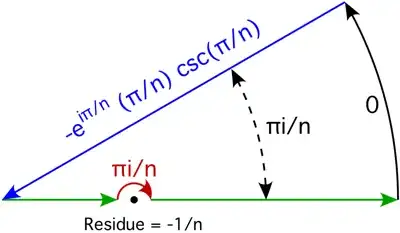
if $n>1$. The last equality $(2)$ follows directly from robjohn's work by letting $x \to \infty$ in $(1)$. So, in summary,

For $x<1$, $$ \int_0^x \frac{du}{1-u^n} = x\cdot{}_2F_1\left(\frac{1}{n},\,1;\,\frac{1}{n}+1;\,x^n\right), $$ and for $x>1$ and $n>1$, $$ \text{PV} \int_0^x \frac{du}{1-u^n} = \frac{x^{1-n}}{n-1}\, {}_2F_1\left(1-\frac{1}{n},\,1;\,2-\frac{1}{n};\,x^{-n}\right) + \frac{\pi}{n} \cot\left(\frac{\pi}{n}\right). $$

In computing their table, they seem to have assumed that $f(n) = 0$. Indeed, their table is exactly equal to the one generated by

$$ g(n,x) = \text{PV} \int_0^x \frac{du}{1-u^n} - \frac{\pi}{n} \cot\left(\frac{\pi}{n}\right). $$

For example,

$$ \begin{align*} g(2.6,1.01) &\approx 1.75625, \\ g(2.6,1.02) &\approx 1.4927, \\ g(2.6,1.03) &\approx 1.33979, \\ g(2.6,1.04) &\approx 1.23215, \\ g(2.6,1.05) &\approx 1.14932. \end{align*} $$

Thanks for the name. I tried writing the series in explicit form. Would it be equal to: $$ \sum_{i=0}^{\infty} \cfrac{1 \cdot 1/n}{1+1/n} \cfrac{(x^n)^i}{i!} $$ ? — osolmaz, Jan 06 '13 at 21:17
Do you know whether for $x\gt1$, this function agrees with the Cauchy Principal Value of the integral? — robjohn, Jan 06 '13 at 22:53
@robjohn it doesn't look like it. Mathematica returns a complex number for the hypergeometric function when $x > 1$. — Antonio Vargas, Jan 06 '13 at 22:54
I just computed the PV from $0$ to $\infty$; it comes to $\frac\pi n\cot\left(\frac\pi n\right)$. — robjohn, Jan 06 '13 at 23:33
@robjohn, do you think the equality in $(*)$ follows from your contour integration? — Antonio Vargas, Jan 07 '13 at 01:01
@AntonioVargas: judging from the previous equation as $x\to\infty$, I would say yes :-) — robjohn, Jan 07 '13 at 01:17
@AntonioVargas & robjohn Amazing work! Thanks for all your efforts. I wish I could give more than just reputation. I must choose this one as the answer, however, since it is a complete solution to the problem. — osolmaz, Jan 07 '13 at 08:44
@AntonioVargas There is a point I could not understand. In $(2)$, how is the expression on the rhs equal to $\mathrm{PV}\int_0^\infty\frac{\mathrm{d}u}{1-u^n}$? — osolmaz, Jan 07 '13 at 11:44
@nrs My deleted comment was correct. I should wait to wake up more before coming here! I'll repost it just below. — Antonio Vargas, Jan 07 '13 at 13:09
The expression in $(1)$ is equal to the PV of the integral as defined at the top of robjohn's answer, where $f(n)$ defined just below by the limit. That $f(n) = (\pi/n)\cot(\pi/n)$ follows from robjohn's calculation that $\text{PV}\int_0^\infty = (\pi/n)\cot(\pi/n)$. Indeed, if $n>1$ then $$\lim_{x \to \infty} \frac{x^{1-n}}{n-1}, {}_2F_1\left(1-\frac{1}{n},,1;,2-\frac{1}{n};,x^{-n}\right) = 0$$ since ${}_2F_1(a,b;c;0) = 1$. So, taking the limit as $x \to \infty$ in equation $(1)$ we are left with $\text{PV}\int_0^\infty = f(n)$, so that we must have $f(n) = (\pi/n)\cot(\pi/n)$. — Antonio Vargas, Jan 07 '13 at 13:10

Analytic integral of diverging function

2 Answers2