Contour solving $\int^{\infty}_0\frac{x^n}{1+x^m}$ for $1

Question

Based on this: https://math.stackexchange.com/a/110465/595084

I was reading through the derivation process of $$\int^{\infty}_0\frac{x^n}{1+x^m}=\frac{\pi}{m} \csc\left(\frac{\pi (n+1)}{m}\right),\qquad n\ge0,\,m>n+1$$ by way of a pizza slice contour.

Since the poles of the complex function(which is just the integrand) is not dependent on the numerator, we just have to look at the denominator, so just fix a $n=0$.

The contour works very well for all $m\ge2$, but from what I see I have a hard time justifying how it would work for $1<m<2$.

Since we have non-integer $m$, our function is multivalued and the answer states that we would take the principal branch, which means there is a branch cut along the negative real axis.

Here's the problem. When $1<m<1.5$, we have a contour similar to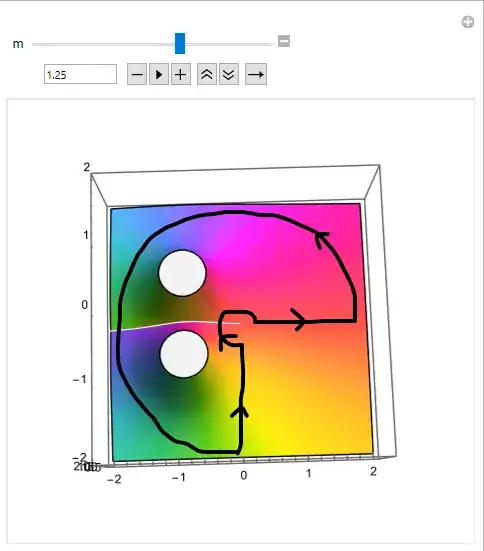

which not only crosses the branch cut twice, and encloses more than $1$ pole. This would obviously invalidate the residue that we get by assuming the contour encloses only $1$ pole.

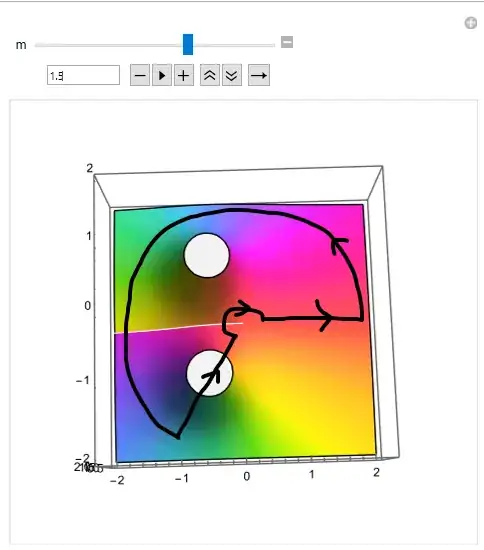
When we have $m=1.5$, we actually integrate through a pole

I'm presuming this wouldn't be much of a problem if we make a small detour around it. The small arc around the pole goes to $0$, and the path coming back to the origin can be thought of in a principal value sense. But we're still integrating past a branch cut.

When $1.5<m<2$, we have a contour that looks like

which still crosses the branch cut twice!

At the integers there is no branch cut and the poles are nicely oriented so we don't have any problems, but in this small interval between 1 and 2, it seems like the contour shouldn't work at all. Yet, I have verified that the integral and formula work for this interval.

Why does it work?

Answer 1

Yes, I think you found a mistake in that linked answer: When $1<m<2$, we need to use a different branch cut of the complex function $z^m$.

The region of integration has $z = re^{i \theta}$ where $\epsilon \leq r \leq R$, $0 \leq \theta \leq \frac{2\pi}{m}$. So to get a function mostly continuous in the region, we can take the branch cut along the ray bisecting the remaining angle between $\frac{2\pi}{m}$ and $2\pi$: With $r, \theta \in \mathbb{R}$ and $r \geq 0$, this branch is given by

$$ (r e^{i\theta})^m = r^m \exp\left(i m \theta - 2im\pi \left\lfloor \frac{\theta}{2\pi} + \frac{m-1}{2m} \right\rfloor\right) $$

Using this meaning of $z^m$, the integrand $f(z) = \frac{z^n}{1+z^m}$ has exactly one pole inside the region of integration, at $z=e^{i \pi/m}$.

For example, suppose $m = \frac{4}{3}$. The region has $0 \leq \theta \leq \frac{3\pi}{2}$, and $f$'s only pole is at $z=e^{3i \pi/4}$. Although some branches of $z^{4/3}$, including the principal branch, have a pole at $z = e^{-3i \pi/4}$, this function $f$ does not: it's defined in terms of a "$z^{4/3}$" branch which gives $e^{-3i\pi/4} \mapsto \exp(\frac{4}{3} \frac{5i \pi}{4}) = e^{-i \pi/3}$ so there is no division by zero.

We also see that along the straight line segment edges of the path of integration where $\theta = 0$ or $\theta = \frac{2\pi}{m}$ ($\Gamma_1$ and $\Gamma_3$ in the linked answer), the chosen branch gives $z^m = 1$, so $f(z) = \frac{z^n}{2}$, and the symmetry argument is allowed. ($f(z)$ has different values on $\Gamma_3$ if the principal branch of $z^m$ is used with $m<2$.)