Compute $\int_0^{+\infty}\frac{x^{\alpha}}{1+x^n}dx$, $0<1+\alpha

Question

I am asked to compute this integral in a sheet that treats the Residue's theorem. I've found the n singularities, calculated the residues, but for example for n=3 and $\alpha = 1$ I get that the sum of the residues is equal to 0, while Wolfram alpha tells me that the integral is different from zero. I am taking into account the branch cut. Any help would be appreciated. I found that the singularities are located at $z_k = e^{i/n (\pi + 2\pi k)}$ and Residue(s)=$\frac{1}{n}e^{(i/n)(\alpha-n+1)(\pi + 2\pi k). To compute the integral I would choose a contour that avoids the branch cut, going from R to a distance epsilon from the 0 just above the branch cut, then do a circle around zer of radius epsilon, then go from there to R under the brunch cut, and then do a circle of Radius R to close everything. I get that $\int_0^{+\infty}\frac{x^{\alpha}}{1+x^n}dx = \frac{e^{(i/n)(\alpha-n+1)(\pi+2\pi k}}{n(1-e^{2\pi i\alpha)}}$, where in the numerator we obviously have to sum over k. But like I said this isn't correct because for $\alpha$ natural this explodes, and this doesn't hold for a particular case of $n,\alpha$

Answer 1

Important Note:

I have come to realize that the sum of residues is actually NOT $0$, but have yet to figure out how to compute it. But as I have already written most of this answer, I shall post it anyway.

---

Since we are going to be working with complex numbers, we will need to define the function $x^\alpha$.

Here, I take the branch cut to be along the positive real axis, so that we can make the definition

$$x^\alpha=|x|^\alpha e^{i \alpha \arg (x)} \qquad \arg (x) \in (0,2\pi)$$

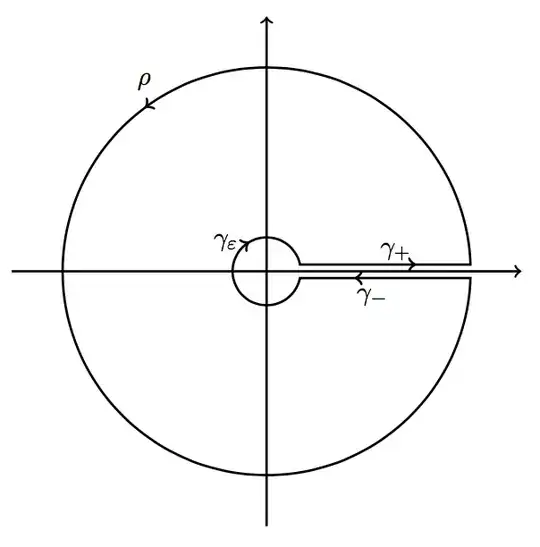
Next, consider the keyhole contour as shown below

where the radius of $\rho$ is $R$, the radius of $\gamma_\epsilon$ is $\epsilon$, and $\gamma_+$ and $\gamma_-$ are respectively just above and just below the positive real axis.

For each $R$ and $\epsilon$, lets call this contour $\Gamma _{R,\epsilon}$.

Let $f(x)=\dfrac{x^\alpha}{1+x^n}$

We see that the singularities of $f$ are at $$x=\exp \bigg[\frac{i\pi}{n}(1+2k) \bigg] \qquad k=0,\dots ,n-1$$

They are all lined up on the unit circle, so as long as $\epsilon<1$ and $R>1$, all of them will be inside our contour.

NOTE: The sum of residues is NOT $0$. I am still trying to figure out how to find the sum of the residues, but for now, lets suppose that the sum of residues is $\Omega$.

Then, by Cauchy's Residue Theorem,

\begin{align} & \int_{\Gamma_{R,\epsilon}}f(x)dx=2\pi i \Omega \qquad \forall \; 0<\epsilon<1 \; \forall \; R>1 \\ \implies & \lim_{R \rightarrow \infty} \lim_{\epsilon \rightarrow 0} \int_{\Gamma_{R,\epsilon}}f(x)dx=2\pi i \Omega \tag{1} \end{align}

Now lets have a look at each individual component of $\Gamma_{R,\epsilon}$

$f$ has no singularities inside $\gamma_\epsilon$. However, it does go from one end of the branch cut to the other, so we cannot just claim that its integral is $0$. Instead, we can use the fact that $\epsilon \rightarrow 0$:

\begin{align} \bigg| \int_{\gamma_\epsilon}\frac{x^\alpha}{1+x^n}dx \bigg| & ≤ \int_{t=0}^{t=2\pi}\bigg| \frac{\epsilon^\alpha e^{it\alpha}}{1+\epsilon^n e^{itn}}i\epsilon e^{it} \bigg| dt \\ & = \epsilon^{\alpha+1} \int_{t=0}^{t=2\pi}\bigg| \frac{1}{1+\epsilon^n e^{itn}}\bigg| dt \\ & ≤ \epsilon^{\alpha+1} \int_{t=0}^{t=2\pi} \frac{1}{1-\epsilon^n}dt \\ & = \frac{2\pi \epsilon^{\alpha+1}}{1-\epsilon^n} \rightarrow 0 \quad \text{as} \; \epsilon \rightarrow 0 \end{align}

Hence

$$\lim_{\epsilon \rightarrow 0} \int_{\gamma_\epsilon} f(x)dx=0 \tag{2}$$

Of course, we can use a similar argument for the big arc $\rho _R$

$$\bigg| \int_{\rho_R}\frac{x^\alpha}{1+x^n}dx \bigg| ≤ \int_{t=0}^{t=2\pi}\bigg| \frac{R^\alpha e^{it\alpha}}{1+R^n e^{itn}}iR e^{it} \bigg| dt ≤ \int_{t=0}^{t=2\pi}\frac{R^{\alpha +1}}{1-R^n}dt=\frac{2\pi R^{\alpha +1}}{1-R^n} \rightarrow 0 \; \text{as} \; R\rightarrow \infty$$

where we have used the fact that $\alpha +1<n$. It follows that

$$\lim_{R \rightarrow \infty} \int_{\rho_R} f(x)dx=0 \tag{3}$$

Next, we observe that the integral along $\gamma_+$ is the one we want. As for the integral along $\gamma_-$, we see that it is parameterised in the opposite direction as $\gamma_+$.

Moreover, look back at our definition of $x^\alpha$. If we were to take a point $x_+$ just above the real axis, and its "corresponding point" $x_-$ just below the real axis, we see that

$$x_-^\alpha = |x_-|^\alpha e^{i\alpha (2\pi)}=e^{i\alpha (2\pi)}\bigg(|x_+|^\alpha e^{i\alpha (0)}\bigg)=e^{i\alpha (2\pi)}x_+^\alpha$$

Hence, we have the relationship

$$\int_{\gamma_-}f(x)dx=-e^{i\alpha (2\pi)}\int_{\gamma_+}f(x)dx \tag{4}$$

FINALLY, if we plug $(2)$, $(3)$ and $(4)$ back into $(1)$, we get

\begin{align} & \lim_{R \rightarrow \infty} \lim_{\epsilon \rightarrow 0}\int_{\Gamma_{R,\epsilon}}f(x)dx=2\pi i \Omega \\ \implies & \lim_{R \rightarrow \infty} \lim_{\epsilon \rightarrow 0} \bigg(\int_{\gamma_\epsilon \, +\, \rho_R \,+\, \gamma_+ \,+\, \gamma_-} f(x)dx \bigg) =2\pi i \Omega \\ \implies & (0)+(0)+\lim_{R \rightarrow \infty} \lim_{\epsilon \rightarrow 0} \bigg(\int_{\gamma_+} f(x)dx + \int_{\gamma_+} f(x)dx \bigg)=2\pi i \Omega \\ \implies & \lim_{R \rightarrow \infty} \lim_{\epsilon \rightarrow 0} \big(1-e^{2\pi i \alpha} \big) \int_{\gamma_+}f(x)dx=2\pi i \Omega \\ \implies & \int_0^\infty \frac{x^\alpha}{1+x^n}dx=\frac{2\pi i \Omega}{1-e^{2\pi i \alpha}} \end{align}

Answer 2

Too long for a comment and moreover using real analysis (I faced this problem years ago).

As given by Wolfram Alpha $$\int\frac{x^a}{1+x^n}\,dx=\frac{x^{a+1} }{a+1}\, _2F_1\left(1,\frac{a+1}{n};\frac{n+a+1}{n};-x^n\right)$$ Using the given bounds $$\int_0^\infty\frac{x^a}{1+x^n}\,dx=\frac{\pi }{n}\csc \left(\frac{\pi (a+1)}{n}\right)\qquad \text{if}\qquad \Re(a-n)<-1\land \Re(a)>-1$$ Amazing is also $$\int_1^\infty\frac{x^a}{1+x^n}\,dx=\frac{H_{-\frac{a+1}{2 n}}-H_{-\frac{n+a+1}{2 n}}}{2 n}\qquad \text{if}\qquad \Re(a-n)<-1\land \Re(a)>-1$$

As Frank W. commented, the problem is much simpler using $x=\tan^{2/n}(t)$ which reduces the problem to $$\frac2n\int_0^{\frac \pi 2} \tan ^{\frac{2 (a+1)}{n}-1}(t)\,dt$$