I believe that I could try to compute the same integral with limits from $-\infty$ to $\infty$ using residue on a half circle and then let the radius tend off to infinity, and once I have that value I should be able to take half of that integral. However, my colleagues have told me that I am wrong. I am not sure how to approach this, with residues, otherwise.
-
I give you the answer $(1+2\sqrt{2})Pi/4$ – Apr 23 '15 at 21:53
-
You could try with a circular sector, centered in 0 with a side on the positive real axis. Something like $\gamma={z\in[0,R]}\cup{z=Re^{it}, t\in(0,\theta)}\cup{z=re^{i\theta},\ r\in[0,R]}$, for a fixed $\theta$ (avoding $\pi/4+k\pi/2$ so you don't intersect the poles), then let $R\to+\infty$. Actually, a wise choice of $\theta$ would be a value such that in that section of the contour you get $z^4=1$. – yellon Apr 23 '15 at 21:55
-
2Because of the $x$ term wich is odd, your integral cannot be half the one from $-\infty$ to $\infty$. – Alex M. Apr 23 '15 at 22:14
3 Answers
It is easier to deal first with the piece: $$\int_{0}^{+\infty}\frac{x}{1+x^4}\,dx = \left.\frac{1}{2}\,\arctan(x^2)\right|_{0}^{+\infty}=\frac{\pi}{4}\tag{1}$$ then compute $\int_{0}^{+\infty}\frac{1+x^2}{1+x^4}\,dx$ through the residue theorem, leading to: $$\int_{0}^{+\infty}\frac{1+x+x^2}{1+x^4}\,dx = \frac{\pi}{4}+\frac{\pi}{\sqrt{2}}. \tag{2}$$
- 353,855
If you accept proofs other than based on the residue theorem, it is known (using Euler's $B$ function; let me know if you want details) that $$\int \limits _0 ^\infty \frac {x^m} {1+x^n} \mathbb{d}x = \frac \pi {n \sin \frac {\pi (m+1)} n}$$. Then if you split your integral in three integrals like the one I am showing, you will get $\frac {{\sqrt 2} \pi} 4 + \frac \pi 4 + \frac {{\sqrt 2} \pi} 4 = \frac \pi 4 + \frac \pi {\sqrt 2}$.
EDIT: To clarify the above integral, one can immediately compute the even more general $$\int \limits _0 ^\infty \frac {x^m} {(1+x^n)^p} \mathbb{d}x = B(\frac {m+1} n, p - \frac {m+1} n)$$ by making the change of variables $t = \frac {x^n} {1+x^n}$. If $p$ has a nice form (for instance if it is natural), the expression can be further simplified by using Beta's recursion properties and the fact that $B(x,1-x) = \frac \pi {\sin \pi x}$. The important point to make here is that all these results involving Euler's functions can be obtained by purely elementary methods, with no need for contour integration in the complex plane.
- 35,207
-
+1 for flipping off residue calc. But, you should have csc instead (better aesthetics). And just being semantically inclined here but the reference "B function" is better known as the beta function – Zach466920 Apr 23 '15 at 22:52
-
1@Zach466920: What is "csc"? There are parts of the world where the "beta" and "gamma" functions are denoted by the corresponding capital Greek letters. – Alex M. Apr 23 '15 at 23:08
-
Touché, it means cosecant by the way. As to your second point, why not denote them by the corresponding letters? – Zach466920 Apr 23 '15 at 23:14
-
@robjohn also provable without contour integration using Ramunijin's master theorem or Euler's reflection formula. – Zach466920 Apr 24 '15 at 00:25
-
@robojon extremely misleading statement. The link you provide has answers referencing a myriad of techniques! – Zach466920 Apr 24 '15 at 00:30
-
@robjohn "The integral you cite above is proven in this answer using contour integration" suggests that this is the only proof given, which obviously isn't true. Just because a question suggests using a certain technique does not make that proof better than other techniques! That's almost like saying a proof of an integral using contour integration is more acceptable than another that uses another technique... – Zach466920 Apr 24 '15 at 14:10
-
@robjohn Yes, to the Op perhaps. All the other people are scratching their heads wondering about the contrived request. – Zach466920 Apr 24 '15 at 17:09
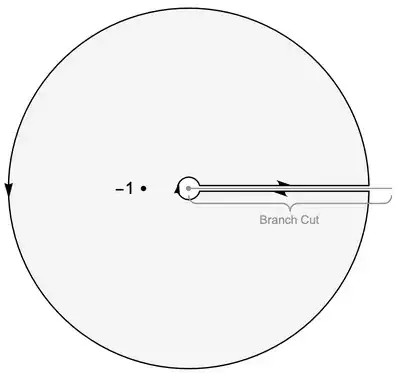
We will use the contour $\gamma$ avoiding the positive real axis,
Change variables $x\mapsto x^{1/4}$ to get $$ \int_0^\infty\frac{1+x+x^2}{1+x^4}\,\mathrm{d}x=\frac14\int_0^\infty\frac{x^{-3/4}+x^{-1/2}+x^{-1/4}}{1+x}\,\mathrm{d}x\tag{1} $$ Then, as in this answer, handle the three integrals $$ \int_0^\infty\frac{x^{-\alpha}}{1+x}\,\mathrm{d}x\tag{2} $$ using $\log(z)=\log(x)$ on the top of the real axis and $\log(z)=\log(x)+2\pi i$ on the bottom. This gives $$ \int_\gamma\frac{z^{-\alpha}}{1+z}\,\mathrm{d}z=\left(1-e^{-2\pi i\alpha}\right)\int_0^\infty\frac{x^{-\alpha}}{1+x}\,\mathrm{d}x\tag{3} $$ since the integral along the large and small circular contours vanish.
We can now use contour integration to say that the contour integral above is equal to the residue at $z=-1$. That is, $$ \int_\gamma\frac{z^{-\alpha}}{1+z}\,\mathrm{d}z=2\pi i\,e^{-\pi i\alpha}\tag{4} $$ Combine $(3)$ and $(4)$ to get $$ \begin{align} \int_0^\infty\frac{x^{-\alpha}}{1+x}\,\mathrm{d}x &=\frac{2\pi i}{e^{\pi i\alpha}-e^{-\pi i\alpha}}\\ &=\frac{\pi}{\sin(\pi\alpha)}\tag{5} \end{align} $$ Use $(5)$ to evaluate the three pieces in $(1)$: $$ \frac14\left(\frac\pi{1/\sqrt2}+\frac\pi{1}+\frac\pi{1/\sqrt2}\right) =\pi\,\frac{1+2\sqrt2}{4}\tag{6} $$
- 345,667