How do I compute
$$\int_0^\infty \frac{(\log x)^2}{1+x^2} dx$$
What I am doing is take
$$f(z)=\frac{(\log z)^2}{1+z^2}$$
and calculating
$\text{Res}(f,z=i) = \dfrac{d}{dz} \dfrac{(\log z)^2}{1+z^2}$ which came out to be $\dfrac{\pi}{2}-\dfrac{i\pi^2}{8}+\dfrac{i\pi}{2}$
Im not too sure how to move on from here. the given answer is $\dfrac{\pi^3}{8}$
For this integral, you want to define you branch cut along the negative x axis and use a contour with a semi circle around the origin.
Also, note we are taking the real Cauchy Principal value. Then $$ \int_0^{\infty}\frac{(\ln(z))^2}{1+z^2}dz = \int_{\Gamma}f(z)dz+\int_{\gamma}f(z)dz + \int_{-\infty}^0f(z)dz + \int_0^{\infty}f(z)dz $$ Let $R$ be the radius of big semi circle, $\Gamma$ and $\delta$ the radius of the small semi circle $\gamma$. When $R\to\infty$, $\int_{\Gamma}\to 0$ and $\int_{\gamma}\to 0$ when $\delta\to 0$ by the estimation lemma. Then $$ \int_{-\infty}^0f(z)dz + \int_0^{\infty}f(z)dz = 2\pi i \sum\text{Res}_{\text{UHP}} $$ where UHP is the upper half plane. There is only one pole in the upper half plane and that is $z = i$ $$ \text{Re PV}\biggl[\int_{-\infty}^0\frac{(\ln|z| + i\pi)^2}{z^2+1}dz + \int_0^{\infty}\frac{(\ln|z| + i\cdot 0)^2}{z^2+1}dz\biggr] = 2\pi i\sum\text{Res}_{\text{UHP}} $$ Recall that $\ln(z) = \ln|z| + i\arg(z)$. Can you take it from here?
Mouse over for solution.
\begin{align}\text{Re PV}\biggl[\int_{-\infty}^0\frac{\ln^2|z| + 2\pi i\ln|z| - \pi^2}{z^2 + 1}dz +\int_0^{\infty}\frac{\ln^2|z|}{z^2 + 1}dz\biggr]&= 2\pi i\lim_{z\to i}(z - i)\frac{(\ln|z| + i\pi/2)^2}{z^2+1}\\2\int_0^{\infty}\frac{\ln^2(x)}{x^2 + 1}dx - \pi^2\int_0^{\infty}\frac{dx}{x^2+1} &= -\frac{\pi^3}{4}\\2\int_0^{\infty}\frac{\ln^2(x)}{x^2 + 1}dx - \frac{\pi^3}{2} &= -\frac{\pi^3}{4}\\\int_0^{\infty}\frac{\ln^2(x)}{x^2 + 1}dx &= \frac{\pi^3}{4} - \frac{\pi^3}{8}\\&= \frac{\pi^3}{8}\end{align}
$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ $\ds{}$ \begin{align} \overbrace{\color{#66f}{\large\int_{0}^{\infty}{\ln^{2}\pars{x} \over 1 + x^{2}}\,\dd x}}^{\ds{\color{#c00000}{x^{2}\ \mapsto\ x}}}&\ =\ \int_{0}^{\infty}{\ln^{2}\pars{x^{1/2}} \over 1 + x}\,\half\,x^{-1/2}\,\dd x ={1 \over 8}\int_{0}^{\infty}{x^{-1/2}\ln^{2}\pars{x} \over 1 + x}\,\dd x \\[5mm]&={1 \over 8}\,\lim_{\mu\ \to\ -1/2}\totald[2]{}{\mu} \color{#c00000}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x}\tag{1} \end{align}
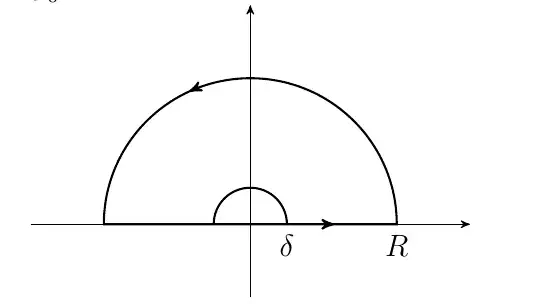
\begin{align}&\color{#c00000}{% \int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} =2\pi\ic\expo{\pi\mu\ic} -\int_{\infty}^{0}{x^{\mu}\expo{2\pi\mu\ic} \over 1 + x}\,\dd x =2\pi\ic\expo{\pi\mu\ic} +\expo{2\pi\mu\ic}\color{#c00000}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} \\[5mm]&\imp\color{#c00000}{\int_{0}^{\infty}{x^{\mu} \over 1 + x}\,\dd x} ={2\pi\ic\expo{\pi\mu\ic} \over 1 - \expo{2\pi\mu\ic}} =\pi\,{2\ic \over \expo{-\pi\mu\ic} - \expo{\pi\mu\ic}}=-\pi\csc\pars{\pi\mu} \end{align}
Replacing in $\pars{1}$: \begin{align} &\color{#66f}{\large\int_{0}^{\infty}{\ln^{2}\pars{x} \over 1 + x^{2}}\,\dd x} ={1 \over 8}\,\lim_{\mu\ \to\ -1/2}\totald[2]{\bracks{-\pi\csc\pars{\pi\mu}}}{\mu} \\[5mm]&={1 \over 8}\,\lim_{\mu\ \to\ -1/2}\braces{-\pi\bracks{% \pi^{2}\cot^{2}\pars{\pi\mu}\csc\pars{\pi\mu} + \pi^{2}\csc^{3}\pars{\pi\mu}}} \\[5mm]&={1 \over 8}\braces{-\pi\bracks{\pi^{2}\csc^{3}\pars{-\,{\pi \over 2}}}} =\color{#66f}{\large{\pi^{3} \over 8}} \end{align}
Using $\beta(3)=\frac{\pi^3}{32}$ from this answer, we can apply $x\mapsto e^{-x}$ to get $$ \begin{align} \int_0^\infty\frac{\log(x)^2}{1+x^2}\,\mathrm{d}x &=\int_{-\infty}^\infty\frac{x^2}{1+e^{-2x}}\,e^{-x}\,\mathrm{d}x\\ &=2\int_0^\infty\frac{x^2}{1+e^{-2x}}\,e^{-x}\,\mathrm{d}x\\ &=2\sum_{k=0}^\infty\int_0^\infty x^2(-1)^ke^{-(2k+1)x}\,\mathrm{d}x\\ &=2\sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)^3}\Gamma(3)\\[6pt] &=2\beta(3)\Gamma(3)\\[9pt] &=\frac{\pi^3}8 \end{align} $$
I would consider the following contour integral
$$\oint_C dz \frac{\log^3{z}}{1+z^2} $$
where $C$ is a keyhole contour of outer radius $R$ and inner radius $\epsilon$, about the positive real axis. Without explicitly showing that the integrals over the outer and inner circles vanish as $R\to\infty$ and $\epsilon \to 0$, the integral is equal to
$$\int_0^{\infty} dx \frac{\log^3{x}-(\log{x}+i 2 \pi)^3}{1+x^2} = -i 6 \pi \int_0^{\infty} dx \frac{\log^2{x}}{1+x^2} + 12 \pi^2 \underbrace{\int_0^{\infty} dx \frac{\log{x}}{1+x^2}}_{0} + \\i 8 \pi^3 \underbrace{\int_0^{\infty} dx \frac{1}{1+x^2}}_{\pi/2} $$
The contour integral is also equal to the sum of the residues of the integrand at the poles $z=\pm i$:
$$-i 6 \pi \int_0^{\infty} dx \frac{\log^2{x}}{1+x^2} + i 4 \pi^4 = i 2 \pi \left (\frac{-i \pi^3/8}{2 i} + \frac{-i 27\pi^3/8}{-2 i} \right ) = i \frac{13 \pi^4}{4}$$
Note that the keyhole contour demands that $\arg{z} \in [0,2\pi]$. Thus,
$$\int_0^{\infty} dx \frac{\log^2{x}}{1+x^2} = \frac{\pi^3}{8} $$
We have $$\int_1^{\infty} \dfrac{\ln^2(x)}{1+x^2}dx = \int_1^0 \dfrac{\ln^2(1/x)}{1+1/x^2} \dfrac{-dx}{x^2} = \int_0^1 \dfrac{\ln^2(x)}{1+x^2}dx$$ Hence, our integral is $$I = 2\int_0^1 \dfrac{\ln^2(x)}{1+x^2}dx$$ From complex analysis, since $\dfrac1{1+z^2}$ is analytic in the open unit disk, we have $$\dfrac1{1+z^2} = \sum_{k=0}^{\infty}(-1)^kz^{2k}$$ Hence, $$I = 2\sum_{k=0}^{\infty}(-1)^k \int_0^1 x^{2k}\ln^2(x)dx = 2\sum_{k=0}^{\infty}(-1)^k \dfrac2{(2k+1)^3} = 2 \cdot 2 \cdot \dfrac{\pi^3}{32} = \dfrac{\pi^3}8$$ where the last equality follows from the fact that $$\text{Li}_n(e^{2\pi ix}) + (-1)^n \text{Li}_n(e^{-2\pi ix}) = -\dfrac{(2 \pi i)^n}{n!} B_n(x)$$ taking $n=3$, $x=1/4$.
