1

Consider the integral:

$$\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} dx$$

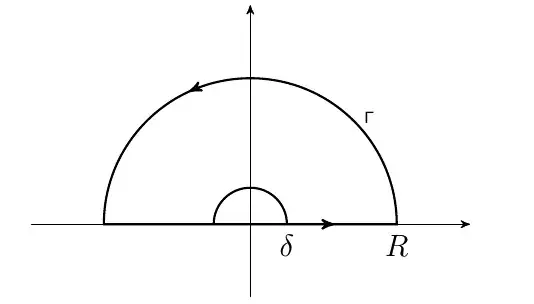
Log contour

Image taken and modified from: Complex Analysis Solution (Please Read for background information).

$R$ is the big radius, $\delta$ is the small radius.

We consider $\displaystyle f(z) = \frac{\log^2(z)}{z^2 + 1}$ where $z = x+ iy$

How can we prove:

$$\oint_{\Gamma} f(z) dz \to 0 \space \text{when} \space R \to \infty$$

We use the parameter (For the big circle $\Gamma$):

$$z = Re^{i\theta}$$

$$\oint_{\Gamma} f(z) dz = \int_{0}^{\pi} \frac{\left( \log(R) + \log(e^{i\theta}) \right)^2\cdot iRe^{i\theta})}{(R^2)(e^{i\theta})^2 + 1} d\theta$$

$$\left| \int_{0}^{\pi} \frac{\left( \log(R) + \log(e^{i\theta}) \right)^2\cdot iRe^{i\theta})}{(R^2)(e^{i\theta})^2 + 1} d\theta \right| < \int_{0}^{\pi} \left| \frac{\left( \log(R) + \log(e^{i\theta}) \right)^2\cdot iRe^{i\theta})}{(R^2)(e^{i\theta})^2 + 1} \right| d\theta$$

We need to try to find:

$$\left| \frac{\left( \log(R) + \log(e^{i\theta}) \right)^2\cdot iRe^{i\theta})}{(Re^{i\theta})^2 + 1} \right|$$

To make the job easier, we can decompose:

$$\left| \frac{\left( \log(R) + \log(e^{i\theta}) \right)^2\cdot iRe^{i\theta})}{(Re^{i\theta})^2 + 1} \right| = \frac{\left|\left( \log(R) + \log(e^{i\theta}) \right)\right| \left| \left( \log(R) + \log(e^{i\theta}) \right) \right| \cdot |iRe^{i\theta}|}{\left| (Re^{i\theta})^2 + 1 \right|} $$

We know: $|iRe^{i\theta}| = R$

$$\frac{\left|\left( \log(R) + \log(e^{i\theta}) \right)\right| \left| \left( \log(R) + \log(e^{i\theta}) \right) \right| \cdot |iRe^{i\theta}|}{\left| (Re^{i\theta})^2 + 1 \right|} < \frac{R}{\left | (Re^{i\theta})^2 + 1 \right |} $$

But how can we find:

$$\left | (Re^{i\theta})^2 + 1 \right |$$

$$\lim_{R \to \infty} \frac{R}{(Re^{i\theta})^2 + 1} = 0$$

Since $R < R^2$ of the denominator.

But I still cant justify:

$$\frac{\left|\left( \log(R) + \log(e^{i\theta}) \right)\right| \left| \left( \log(R) + \log(e^{i\theta}) \right) \right| \cdot |iRe^{i\theta}|}{\left| (Re^{i\theta})^2 + 1 \right|} < \frac{R}{\left | (Re^{i\theta})^2 + 1 \right |} $$

I just need to prove somehow:

$$\left| \left( \log(R) + \log(e^{i\theta}) \right) \right | < 1$$

Can someone give me a hand?

Community
  • 1
Amad27
  • 10,465

1 Answers1

3

You are overcomplicating things. If $|z|=R$, then $|z^2+1|\geq R^2-1$ and $|\log z|\leq\sqrt{\log^2R+\pi^2}$. This is enough to state that $$\lim_{R\to+\infty}\oint_\Gamma f(z)\,dz=0.$$ This happens because, assuming $z\in\Gamma$ so that $z=Re^{i\theta}$ with $\theta\in[0,\pi]$, and assuming $R\geq e^{\pi}$, $$ |f(z)|\leq\frac{\sqrt{\log^2 R+\pi^2}}{R^2-1}\leq\frac{\sqrt{2}\log R}{R^2\left(1-\frac{1}{e^{2\pi}}\right)}<\frac{3}{2}\cdot\frac{\log R}{R^2},$$ so: $$\left|\oint_{\Gamma}f(z)\,dz\right|<\frac{3\pi}{2}\cdot\frac{\log R}{R}.$$

Jack D'Aurizio
  • 353,855