Integral along a contour is $0$, how?

Question

I recently had an extremely failed attempt at asking the same question, so I am posting the same question more or less to hope that someone can give me feedback.

Consider the integral:

$$\int_{0}^{\infty} \frac{\log^2(x)}{x^2 + 1} dx$$

$\hskip1in$

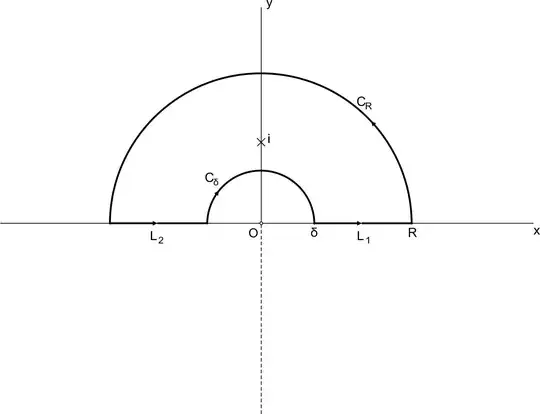
Image taken and modified from: Complex Analysis Solution (Please Read for background information).

$R$ is the big radius, $\delta$ is the small radius.

Actually, lets consider $u$ the small radius. Let $\delta = u$

Ultimately the goal is to let $u \to 0$

We can parametrize,

$$z = ue^{i\theta}$$

$$\int_{\delta} f(z)dz = (-)\cdot\int_{0}^{\pi} \frac{(i\theta + \log(u))^2\cdot (uie^{i\theta})}{(ue^{i\theta})^2 + 1} d\theta$$

$$\left | \int_{0}^{\pi} \frac{(i\theta + \log(u))^2\cdot (uie^{i\theta})}{(ue^{i\theta})^2 + 1} d\theta \right | \le \int_{0}^{\pi} \frac{|(i\theta + \log(u))|^2\cdot(u)}{|(ue^{i\theta})^2 + 1 |} d\theta$$

$$|(ue^{i\theta})^2 + 1 | < u^2 + 1 $$

$$\frac{1}{u^2 + 1} < \frac{1}{|(ue^{i\theta})^2 + 1 |}$$

Since the maximum value of $\theta$ is $\theta = \pi$

$$|(i\theta + \log(u))| = \sqrt{\log^2(u) - \theta^2} \le \sqrt{\log^2(u) + \pi^2}$$

So:

$$|(i\theta + \log(u))|^2 \le \log^2(u) + \pi^2$$

Then:

$$|(i\theta + \log(u))|^2 \le \log^2(u) + \pi^2$$

For values $u$ near $0$.

$$(u)|(i\theta + \log(u))|^2 \le (\log^2(u) + \pi^2)u \le (\pi^2)u + 5\pi^2$$

Therefore,

$$\frac{|\log(z)|}{|z^2 + 1|} \le \frac{(\pi^2)u + 5\pi^2}{u^2 + 1}$$

Then we take the limit as $u \to 0$ which makes the RHS of the inequality 0.

hence the LHS upperbound is $0$.

So is the contour integral around the small semi circle $\delta = 0$?

How do I do this?

Thanks

Answer 1

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\dsc}[1]{\displaystyle{\color{red}{#1}}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\Li}[1]{\,{\rm Li}_{#1}} \newcommand{\norm}[1]{\left\vert\left\vert\, #1\,\right\vert\right\vert} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$

According to your picture you have chosen a $\ds{\ln\pars{z}}$-branch as follows: $$ \ln\pars{z}=\ln\pars{\verts{z}} + \,{\rm Arg}\pars{z}\ic\,\quad z \not= 0\,,\quad -\,{\pi \over 2} < \,{\rm Arg}\pars{z} < {3\pi \over 2} $$

\begin{align}&\int_{C}{\ln^{2}\pars{z} \over z^{2} + 1}\,\dd x =2\pi\ic\,{\bracks{\ln\pars{1} + \pi\ic/2}^{2} \over 2\ic}=-\,{\pi^{3} \over 4} \end{align}

Moreover,

\begin{align} -\,{\pi^{3} \over 4}&=\lim_{\epsilon\ \to\ 0^{+}}\left[\int_{-\infty}^{-\epsilon}{\bracks{\ln\pars{-x} + \pi\ic}^{2} \over x^{2} + 1}\,\dd x\right. \\[5mm]&\left.\phantom{\lim_{\epsilon\ \to\ 0^{+}}\left[A\right.} +\ \underbrace{% \int_{\pi}^{0}{\bracks{\ln\pars{\epsilon} + \ic\theta}^{2}\over \epsilon^{2}\expo{2\ic\theta} + 1}\,\epsilon\expo{\ic\theta}\ic\,\dd\theta} _{\ds{\dsc{\to\ 0}\ \mbox{when}\ \dsc{\epsilon \to 0^{+}}. \mbox{See below.}}} +\int_{\epsilon}^{\infty}{\bracks{\ln\pars{x} + 0\ic}^{2} \over x^{2} + 1}\,\dd x\right] \\[1cm]&=\int_{0}^{\infty} {\ln^{2}\pars{x} + \bracks{\ln\pars{x} + \pi\ic}^{2} \over x^{2} + 1}\,\dd x \\[5mm]&=2\int_{0}^{\infty}{\ln^{2}\pars{x} \over x^{2} + 1}\,\dd x +2\pi\ic\ \overbrace{\int_{0}^{\infty}{\ln\pars{x} \over x^{2} + 1}\,\dd x} ^{\ds{=\ \dsc{0}}}\ -\ \pi^{2}\ \overbrace{\int_{0}^{\infty}{\dd x \over x^{2} + 1}} ^{\ds{=\ \dsc{\pi \over 2}}} \\[5mm]&=2\int_{0}^{\infty}{\ln^{2}\pars{x} \over x^{2} + 1}\,\dd x -{\pi^{3} \over 2}\quad\imp\quad \color{#66f}{\large\int_{0}^{\infty}{\ln^{2}\pars{x} \over x^{2} + 1}\,\dd x} =\half\pars{{\pi^{3} \over 2} - {\pi^{3} \over 4}} =\color{#66f}{\large{\pi^{3} \over 8}} \end{align}

The integral in the small semicircle satisfies $\ds{\pars{~\mbox{with}\ 0 < \epsilon < 1~}}$:

\begin{align} 0&<\verts{\int_{\pi}^{0}{\bracks{\ln\pars{\epsilon} + \ic\theta}^{2}\over \epsilon^{2}\expo{2\ic\theta} + 1}\,\epsilon\expo{\ic\theta}\ic\,\dd\theta}< \epsilon\int_{0}^{\pi}{\bracks{\ln\pars{\epsilon} + \ic\theta}^{2}\over \verts{\epsilon^{2}\expo{2\ic\theta} + 1}}\,\dd\theta \\[5mm]&<{\epsilon \over 1 - \epsilon^{2}} \bracks{\pi\ln^{2}\pars{\epsilon} + \pi^{2}\verts{\ln\pars{\epsilon}} + {\pi^{3} \over 3}}\quad\to\quad 0\quad\mbox{when}\quad\epsilon\to 0^{+}. \end{align}

Answer 2

We want to show that $$\int_{0}^{\infty}\frac{\ln^2 x}{x^2+1} = \frac{\pi^3}{8} \tag{1}$$

Breaking through, let's take $f(z) = \frac{\ln z}{z^2+1}$ with branch $\Big(|z|> 0 -\frac{\pi}{2} < \arg z < \frac{3\pi}{2}\Big)$ of the multiple-valued function $\ln z / (z^2+1)$. As long as we are isolating $z = i$ we're going to take $\delta < 1 < R$. According to Cauchy's Residue Theorem,

$$\int_{L_1} f(z)dz + \int_{C_R} f(z)dz + \int_{L_2} f(z)dz + \int_{C_\delta} f(z)dz= 2\pi i Res_{z=i}f(z)$$

That is,

$$\int_{L_1} f(z)dz + \int_{L_2} f(z)dz = 2\pi i Res_{z=i}f(z) - \int_{C_R} f(z)dz - \int_{C_\delta} f(z)dz \tag{2}$$

Since $$f(z) = \frac{(\ln r + i\theta)^2}{r^2e^{i0} + 1} \ \ \ \ \ \ (z=re^{i\theta})$$

the parametric representations

$$z = r e^{i0} = r \ \ (\delta\leq r\leq R) \ \ \text{and}\ \ z = re^{i\pi} = -r \ \ (\delta\leq r \leq R)$$

for the legs $L_1$ and $-L_2$ can be used to write the LHS pf equation $(2)$ as

$$\int_{L_1} f(z)dz - \int_{-L_2} f(z)dz = \int_{\delta}^{R} \frac{\ln^2 r}{r^2 + 1}dr + \int_{\delta}^{R} \frac{(\ln r + i\pi)^2}{r^2 + 1}dr$$

Also, since

$$Res_{z=i}f(z) = \frac{p(z)}{\phi'(z)}\ \ \text{where}\ \ p(z) = \ln^2 z \ \ \text{and}\ \ \phi(z) = z^2 + 1$$

then

$$Res_{z=i}f(z) = \frac{\Big(\ln (1) + i\frac{\pi}{2}\Big)^2}{2i}$$

Thus equation $(2)$ becomes

$$\begin{align}&2\int_{\delta}^{R} \frac{\ln^2 r}{r^2 + 1}dr + 2\pi i\int_{\delta}^{R} \frac{\ln r }{r^2 + 1}dr - \pi^2\int_{\delta}^{R} \frac{1}{r^2 + 1}dr\\ & = 2\pi i \frac{\Big(\ln (1) + i\frac{\pi}{2}\Big)^2}{2i} - \int_{C_R} f(z)dz - \int_{C_\delta} f(z)dz \\ &= -\frac{\pi^3}{4} - \int_{C_R} f(z)dz - \int_{C_\delta} f(z)dz \end{align}$$

Evaluating integrals

1- $\lim_{\delta \to 0}_{R\to \infty}\int_{\delta}^{R} \frac{\ln r }{r^2 + 1}dr = 0$

2- $\lim_{\delta \to 0}_{R \to \infty}\int_{\delta}^{R} \frac{1}{r^2 + 1}dr = \frac{\pi}{2}$

3- $\lim_{R\to\infty}\int_{C_R} f(z)dz = 0 $

4- $\lim_{\delta \to 0}\int_{C_\delta} f(z)dz = 0 $

Showing $4$.

Take $z = \delta e^{i\theta}$. Notice that if $\delta < 1$ and $z = \delta e^{i\theta}$, $$\begin{align}|\log^2 z| &=|(\ln \delta + i\theta )^2| = |\ln^2\delta + 2i\theta\ln\delta - \theta^2|\\&\leq |\ln^2\delta| + 2|i\theta\ln\delta|+\theta^2 \leq \ln^2\delta -2\pi\ln \delta + \pi^2\end{align}$$ and $$|z^2+1| \geq ||z^2| - 1| = 1 - \delta^2$$ then

$$\Bigg|\int_{C_\delta} f(z)dz\Bigg| \leq \int_{C_\delta} |f(z)| |dz| \leq \frac{\ln^2\delta -2\pi\ln \delta + \pi^2}{1 - \delta^2} \pi\delta$$

the RHS of the inequality goes to $0$ as $\delta \to 0$.

There fore we get

$$2\int_{0}^{\infty} \frac{\ln^2 r}{r^2 + 1}dr = \frac{\pi^3}{4} \Rightarrow \int_{0}^{\infty} \frac{\ln^2 r}{r^2 + 1}dr = \frac{\pi^3}{8}$$