Contour Integration $\int_0^1\frac1{\sqrt[n]{1-x^n}}dx$

Question

I want to compute:

$$\int^{1}_{0}\frac{1}{\sqrt[n]{1-x^n}}dx$$

for natural $n>1$ using Residue Calculus.

I am thinking of using some kind of a keyhole or bone contour that could go around the $n$th roots of unity (singularities in this case). The problem is I believe it is not clear how to define a suitable branch (or branches) of $\log$ in this region for it to work, also considering we only care about the segment from $0$ to $1$.

Answer 1

Here is another contour integration using the contour that arises from not using any substitution.

Using the diagram and contour below, where $f(z)=\frac1{(1-z^n)^{1/n}}$

$\hspace{4cm}$

it is easy to see that the integral along the red contour is $$ \begin{align} &\int_0^1\frac{\mathrm{d}t}{(1-t^n)^{1/n}}-e^{2\pi i/n}\int_0^1\frac{\mathrm{d}t}{(1-t^n)^{1/n}}\\ &=\left(1-e^{2\pi i/n}\right)\int_0^1\frac{\mathrm{d}t}{(1-t^n)^{1/n}}\tag{1} \end{align} $$ The integrand along each successive arm clockwise is $e^{2\pi i/n}$ times the integrand from the previous arm. $\mathrm{d}z$ along each successive arm is $e^{-2\pi i/n}$ times $\mathrm{d}z$ from the previous arm. Therefore, the integral along each successive arm is the same as the integral from the previous arm. Thus, the total of the integral along all the arms is $$ n\left(1-e^{2\pi i/n}\right)\int_0^1\frac{\mathrm{d}t}{(1-t^n)^{1/n}}\tag{2} $$ Now, if $z$ follows a circle of radius $R$ as $R\to\infty$, $f(z)\sim\frac{e^{\pi i/n}}z$ so the integral along a large clockwise circle is $$ -2\pi ie^{\pi i/n}\tag{3} $$ Since $(2)$ is equal to $(3)$, we have $$ \begin{align} \int_0^1\frac{\mathrm{d}t}{(1-t^n)^{1/n}} &=\frac{-2\pi ie^{\pi i/n}}{n\left(1-e^{2\pi i/n}\right)}\\ &=\frac\pi{n\sin(\pi/n)}\tag{4} \end{align} $$

---

The Branch Cut

Consider the function defined by $$ \begin{align} g(z) &=\pi i-\log(1-2^{-n})+\int_2^z\left(\vphantom{\sum_{k=0}^{n-1}}\right.\overbrace{\vphantom{\sum_{k=0}^{n-1}}\frac nw}^{\text{residue$=n$}}+\overbrace{\sum_{k=0}^{n-1}\frac1{e^{2\pi ik/n}-w}}^{\text{residue$=-n$}}\left.\vphantom{\sum_{k=0}^{n-1}}\right)\,\mathrm{d}w\\ &=\log\left(\frac{z^n}{1-z^n}\right)\tag{5} \end{align} $$ $g$ is well defined as long as the path of integration does not circle any of the poles of the integrand, or circles them all (since the sum of the residues is $0$); that is, the poles at $0$ and $\{e^{2\pi ik/n}:k\in\mathbb{Z}\}$. Circling none or all of these points is guaranteed by the branch cut in the diagram above. Therefore, with the branch cuts in the diagram above, $(5)$ allows us to define $$ \frac1ze^{g(z)/n}=\frac1{(1-z^n)^{1/n}}\tag{6} $$

Answer 2

Using the substitution $$ x^n=\frac{z^n}{1+z^n}\qquad\text{and}\qquad\mathrm{d}x=\frac{\mathrm{d}z}{(1+z^n)^{1+1/n}} $$ we get $$ \begin{align} \int_0^1\frac{\color{#00A000}{\mathrm{d}x}}{\color{#C00000}{(1-x^n)^{1/n}}} &=\int_0^\infty\color{#C00000}{(1+z^n)^{1/n}}\color{#00A000}{\frac{\mathrm{d}z}{(1+z^n)^{1+1/n}}}\\ &=\int_0^\infty\frac{\mathrm{d}z}{1+z^n}\\[6pt] &=\frac\pi{n\sin(\pi/n)} \end{align} $$ Using the result of the contour integration in this answer, which says $$ \int_0^\infty\frac{x^m}{1+x^n}\,\mathrm{d}x=\frac{\pi}{n}\csc\left(\pi\frac{m+1}{n}\right) $$

Answer 3

In questions like this one, in order to avoid the problems of defining the right branch of the logarithm or the $n$th root, I suggest to, first start with a change of variables and to use Residue Theorem afterwards.

So, here how I do this. First the change of variables $x^n=\dfrac{e^t}{1+e^t}$ we get $$ I_n~{\buildrel {\rm def}\over =}~\int_0^1\frac{dx}{\root{n}\of{1-x^n}}=\frac{1}{n}\int_{-\infty}^\infty \frac{e^{t/n}}{1+e^t}dt $$ Next we integrate $F(z)=\dfrac{e^{z/n}}{n(1+e^z)}$ on the rectangle $\Gamma_R$ with vertexes $-R$, $R$,$R+2i\pi$ and $-R+2i\pi$. Letting $R$ tend to $+\infty$ we get $$ I_n-e^{2i\pi/n}I_n=2i\pi~\hbox{Res}(F(z),i\pi)=-2i\frac{\pi}{n} e^{i\pi/n}. $$ This yields $$I_n=\frac{\pi}{n\sin(\pi/n)}.$$ Note that we didn't use the fact that $n$ is a natural number. This is valid for any real $n>1$.

Answer 4

$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ \begin{align}& \overbrace{\color{#c00000}{\int_{0}^{1}{\dd x \over \root[n]{1 - x^{n}}}\dd x}} ^{\ds{x^{n}\ \mapsto\ x}}\ =\ \int_{0}^{1}\pars{1 - x}^{-1/n}\,{1 \over n}\,x^{1/n - 1}\,\dd x ={1 \over n}\color{#00f}{\int_{0}^{1}x^{1/n - 1}\pars{1 - x}^{-1/n}\,\dd x} \,\,\,\,\,\pars{1} \end{align}

Now, we study the integral $$ \oint_{\rm DB}{z^{1/n}\pars{1 - z}^{-1/n} \over z}\,\dd z $$ where $\ds{\rm DB}$ is a "dumbbell contour" ( see picture ).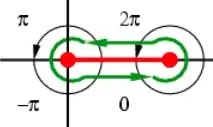

Also, $$ \begin{array}{rclrcccl} z^{1/n} & = & \verts{z}^{1/n}\expo{{\rm Arg}\pars{z}/n}\,, & -\pi & < & {\rm Arg}\pars{z} & < & \pi\,,\quad z \not= 0 \\[2mm] \pars{1 - z}^{-1/n} & = & \verts{1 - z}^{-1/n}\expo{-{\rm Arg}\pars{1 - z}/n}\,, & 0 & < & {\rm Arg}\pars{1 - z} & < & 2\pi\,,\quad z \not= 1 \end{array} $$ It's clear that the product $\ds{z^{1/n}\pars{1 - z}^{-1/n}}$ has a branch-cut in $\bracks{0,1}$.

The integral above the "upper line' is given by $$ \int_{1}^{0}x^{1/n - 1}\pars{1 - x}^{-1/n}\expo{-2\pi\ic/n}\,\dd x = -\expo{-2\pi\ic/n}\color{#00f}{\int_{0}^{1}x^{1/n}\pars{1 - x}^{-1/n}\,\dd x} $$ and in the "lower line" by $\ds{\color{#00f}{\int_{0}^{1}x^{1/n}\pars{1 - x}^{-1/n}\,\dd x}}$. Integration around the semicircles, with centers at $\ds{z = 0}$ and $\ds{z = 1}$, vanishes out when their radius $\ds{\to 0^{+}}$.

Then, \begin{align} &\pars{1 - \expo{-2\pi\ic/n}}\color{#00f}{% \int_{0}^{1}x^{1/n - 1}\pars{1 - x}^{-1/n}\,\dd x} =-2\pi\ic\, {\rm Res}_{\verts{z}\ \to\ \infty}\bracks{z^{1/n - 1}\pars{1 - z}^{-1/n}} \\[3mm]&=-2\pi\ic\,{\rm Res}_{z\ =\ 0}\bracks{% -\,{1 \over z^{2}}\,z^{1 - 1/n}\pars{1 - {1 \over z}}^{-1/n}} =2\pi\ic\,{\rm Res}_{z\ =\ 0}\bracks{\pars{z - 1}^{-1/n} \over z} \\[3mm]&=2\pi\ic\, {\rm Res}_{z\ =\ 0}\bracks{\verts{z - 1}^{\,-1/n}\expo{-\pi\ic/n} \over z} =2\pi\ic\expo{-\pi\ic/n} \end{align}

Then $$ \color{#00f}{\int_{0}^{1}x^{1/n - 1}\pars{1 - x}^{-1/n}\,\dd x} ={2\pi\ic\expo{-\pi\ic/n} \over 1 - \expo{-2\pi\ic/n}} =\pi\,{2\ic \over \expo{\pi\ic/n} - \expo{-\pi\ic/n}} ={\pi \over \sin\pars{\pi/n}} $$ which is replaced in expression $\pars{1}$:

$$ \color{#00f}{\large\int_{0}^{1}{\dd x \over \root[n]{1 - x^{n}}}\dd x ={\pi \over n\sin\pars{\pi/n}}} $$

Answer 5

From Omran Kouba's answer, we have \begin{eqnarray} I_n&=&\frac{1}{n}\int_{-\infty}^\infty \frac{e^{t/n}}{1+e^t}dt=\frac{1}{n}\int_{0}^\infty \frac{e^{t/n}}{1+e^t}dt+\frac{1}{n}\int_{-\infty}^0 \frac{e^{t/n}}{1+e^t}dt\\ &=&\frac{1}{n}\int_{0}^\infty \frac{e^{t/n-1}}{1+e^{-t}}dt+\frac{1}{n}\int_{-\infty}^0 \frac{e^{t/n}}{1+e^t}dt\\ &=&\frac{1}{n}\int_{0}^\infty \sum_{k=0}^\infty(-1)^ke^{t/n-t-kt}dt+\frac{1}{n}\int_{-\infty}^0 \sum_{k=0}^\infty(-1)^ke^{t/n+kt}dt\\ &=&\sum_{k=0}^\infty(-1)^k\frac{1}{nk+1}+\sum_{k=0}^\infty(-1)^k\frac{1}{nk+n-1}\\ &=&\sum_{k=-\infty}^\infty(-1)^k\frac{1}{nk+1}=\frac{\pi}{n\sin\frac{\pi}{n}}. \end{eqnarray}