17

It is known that \begin{align} \arcsin x + \arcsin y =\begin{cases} \arcsin( x\sqrt{1-y^2} + y\sqrt{1-x^2}) \\\quad\text{if } x^2+y^2 \le 1 &\text{or} &(x^2+y^2 > 1 &\text{and} &xy< 0);\\ \pi - \arcsin( x\sqrt{1-y^2} + y\sqrt{1-x^2}) \\\quad\text{if } x^2+y^2 > 1&\text{and} &0< x,y \le 1;\\ -\pi - \arcsin( x\sqrt{1-y^2} + y\sqrt{1-x^2}) \\\quad\text{if } x^2+y^2 > 1&\text{and} &-1\le x,y < 0. \end{cases} \end{align}

I tried to prove this myself, have no problem in getting the 'crux' $\arcsin( x\sqrt{1-y^2} + y\sqrt{1-x^2})$ part of the RHS, but face trouble in checking the range of that 'crux' under the given conditions.

Parth Thakkar
  • 4,452
  • 3
  • 33
  • 50

4 Answers4

20

Using this, $\displaystyle-\frac\pi2\leq \arcsin z\le\frac\pi2 $ for $-1\le z\le1$

So, $\displaystyle-\pi\le\arcsin x+\arcsin y\le\pi$

Again, $\displaystyle\arcsin x+\arcsin y= \begin{cases} \\-\pi- \arcsin(x\sqrt{1-y^2}+y\sqrt{1-x^2})& \mbox{if } -\pi\le\arcsin x+\arcsin y<-\frac\pi2\\ \arcsin(x\sqrt{1-y^2}+y\sqrt{1-x^2}) &\mbox{if } -\frac\pi2\le\arcsin x+\arcsin y\le\frac\pi2 \\ \pi- \arcsin(x\sqrt{1-y^2}+y\sqrt{1-x^2})& \mbox{if }\frac\pi2<\arcsin x+\arcsin y\le\pi \end{cases} $

and as like other trigonometric ratios are $\ge0$ for the angles in $\left[0,\frac\pi2\right]$

So, $\displaystyle\arcsin z\begin{cases}\text{lies in } \left[0,\frac\pi2\right] &\mbox{if } z\ge0 \\ \text{lies in } \left[-\frac\pi2,0\right] & \mbox{if } z<0 \end{cases} $

Case $(i):$ Observe that if $\displaystyle x\cdot y<0\ \ \ \ (1)$ i.e., $x,y$ are of opposite sign, $\displaystyle -\frac\pi2\le\arcsin x+\arcsin y\le\frac\pi2$

Case $(ii):$ If $x>0,y>0$ $\displaystyle \arcsin x+\arcsin y$ will be $\displaystyle \le\frac\pi2$ according as $\displaystyle \arcsin x\le\frac\pi2-\arcsin y$

But as $\displaystyle\arcsin y+\arccos y=\frac\pi2,$ we need $\displaystyle \arcsin x\le\arccos y$

Again as the principal value of inverse cosine ratio lies in $\in[0,\pi],$ $\displaystyle\arccos y=\arcsin(+\sqrt{1-y^2})\implies \arcsin x\le\arcsin\sqrt{1-y^2}$

Now as sine ratio is increasing in $\displaystyle \left[0,\frac\pi2\right],$ we need $\displaystyle x\le\sqrt{1-y^2}\iff x^2\le1-y^2$ as $x,y>0$

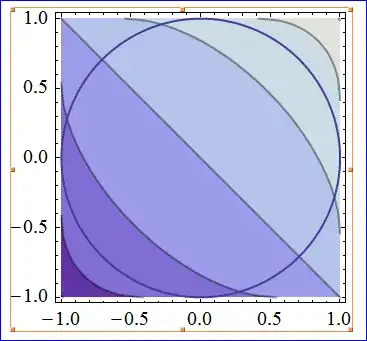
$\displaystyle\implies x^2+y^2\le1 \ \ \ \ (2)$

So, $(1),(2)$ are the required condition for $\displaystyle \arcsin x+\arcsin y\le\frac\pi2$

Case $(iii):$

Now as $\displaystyle-\frac\pi2\arcsin(-u)\le\frac\pi2 \iff -\frac\pi2\arcsin(u)\le\frac\pi2$

$\arcsin(-u)=-\arcsin u$

Use this fact to find the similar condition when $x<0,y<0$ setting $x=-X,y=-Y$

Soham
  • 9,990
lab bhattacharjee
  • 274,582
  • If there is any, I'll surely ask. I'll work it out myself first so that there is no scope of doubt. What I asked was just by going through your answer.

    But I think it's pretty fine now. Thanks!

     – Parth Thakkar Feb 13 '14 at 07:28
  • In the first case, by the condition $xy<0$ alone we have the proper range. That is, $\arcsin(x\sqrt{1-y^2} + y\sqrt{1-x^2}) \in [-\pi/2, \pi/2]$. Then why is that additional condition $x^2 + y^2 > 1$ required? – Parth Thakkar Feb 13 '14 at 07:34
  • 1
    @ParthThakkar, its not required, the condition is either $x^2+y^2\le1$ or ($xy<0$ where $x^2+y^2$ is obviously $>1$) – lab bhattacharjee Feb 13 '14 at 07:57
  • @labbhattacharjee: Wouldn't there be $\le$ sign in your first relation? –  Mar 03 '16 at 08:24
  • @user36790, The equality has been catered in the second – lab bhattacharjee Mar 03 '16 at 08:49
  • 1
    @labbhattacharjee How did you write when $x \gt 0$ and $y \gt 0$ $arcsin(x)+arc(siny) \le \frac{\pi}{2}$ for suppose when $x=1$ and $y=1$ $arcsin(x)+arc(siny)=\pi$ right? can you explain – Umesh shankar Apr 29 '17 at 17:39
  • @Umeshshankar, We also need $(1),(2)$ – lab bhattacharjee Apr 29 '17 at 17:46
  • Ok fine when $xy \lt 0$ you said obviously $x^2+y^2 \gt 1$ i could not get this can you explain – Umesh shankar May 05 '17 at 02:14
  • @Umeshshankar, Which u r talking about? – lab bhattacharjee May 05 '17 at 05:44
  • I am talking about your reply to Parth thakkar in your first comment above – Umesh shankar May 05 '17 at 17:28
  • @Umesh, As it is the else case of $$x^2+y^2\le1$$ – lab bhattacharjee May 05 '17 at 17:35
  • @labbhattacharjee how to get the. conditions on a and y for the case $-\pi<\arcsin(x)+\arcsin(y)<-\pi/2$ –  May 08 '20 at 13:41
  • @lindaOiladali, Have you identified for $$\dfrac\pi2<\arcsin x+\arcsin y<\pi$$ Then use $$\arcsin(-x)=-\arcsin x$$ – lab bhattacharjee May 08 '20 at 13:44
  • @labbhattacharjee i have the same question for $\pi/2<arcsin(x)+arcsin(y)<\pi$ how to get that $x^2+y^2>1$ and $0<x,y\leq1$ –  May 08 '20 at 13:46
  • @lindaOiladali, If $\arcsin x+\arcsin y>\dfrac\pi2; x,y$ must be $>0$

    $$\iff\arcsin x>\dfrac\pi2-\arcsin y=\arccos(y)$$

    Now for $y\ge0,$ $$\arccos(y)=\arcsin\sqrt{1-y^2}$$

    So, we need $$\arcsin(x)>\arcsin\sqrt{1-y^2}$$

    As $\arcsin(x)$ is increasing function, $$x>\sqrt{1-y^2}\implies x^2>1-y^2$$

     – lab bhattacharjee May 08 '20 at 13:55
  • @labbhattacharjee but if $x\leq 0$ and $y\leq 0$ we get the same thing no? –  May 11 '20 at 10:46
  • @lindaOiladali, If both $x,y\le0,$ $$\arcsin x+\arcsin y\le0$$ right? – lab bhattacharjee May 11 '20 at 10:57
  • @labbhattacharjee right I understand, please in my exercise the question is "study according to a and b, the existence of solution for the equation arcsin(x)=arcsin(a)+arcsin(b), " so I must study only the case where $-\pi/2\leq arcsin(a)+arcsin(b)\leq\pi/2$ right? –  May 11 '20 at 11:47
  • Hi. In case (ii), when $x,y\gt0$, shouldn't $arcsin x+arcsin y$ be less than $\pi$, instead of $\frac\pi2$? Because $arcsin x\lt\frac\pi2$ and $\arcsin y\lt\frac\pi2$ – aarbee Jan 25 '22 at 20:17
  • @aarbee, I didn't say, it will be $<\dfrac\pi2$ but I wanted to check when that will be held true . – lab bhattacharjee Jan 26 '22 at 18:46
5

Let $a=\sin^{-1}x,$ $b=\sin^{-1}y\implies\sin a=x,$ $\sin b=y$ and $a,b\in[-\pi/2,\pi/2]\implies a+b\in[-\pi,\pi]$ $$ \sin(a+b)=\sin a\cos b+\cos a\sin b=x\sqrt{1-y^2}+y\sqrt{1-x^2}\\=\sin\bigg[\sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)\bigg]\\ \implies a+b=\color{red}{\sin^{-1}x+\sin^{-1}y=n\pi+(-1)^n\sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)} $$ Case 1: $-\dfrac{\pi}{2}\leq\sin^{-1}x+\sin^{-1}y\leq\dfrac{\pi}{2}$ $$ \color{darkblue}{\sin^{-1}x+\sin^{-1}y=\sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)} $$ $$ \cos(a+b)\geq0\implies \cos a\cos b-\sin a\sin b\geq0\implies \cos a\cos b\geq\sin a\sin b\\ \sqrt{1-x^2}\sqrt{1-y^2}\geq xy\implies\\ a)\ 1-x^2-y^2+x^2y^2-x^2y^2\geq0 \implies x^2+y^2\leq1\\ b)\ 1-x^2-y^2+x^2y^2-x^2y^2<0 \implies x^2+y^2>1, xy<0 $$ Case 2 & 3: $\dfrac{\pi}{2}<\sin^{-1}x+\sin^{-1}y\leq\pi$ and $-\pi\leq\sin^{-1}x+\sin^{-1}y<-\dfrac{\pi}{2}$ $$ \cos(a+b)<0\implies x^2+y^2>1 $$

Case 2-: $\dfrac{\pi}{2}<\sin^{-1}x+\sin^{-1}y\leq\pi$ $$ \sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)=\pi-(\sin^{-1}x+\sin^{-1}y)\\ \implies \color{darkblue}{\sin^{-1}x+\sin^{-1}y=\pi-\sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)} $$ $$ \dfrac{\pi}{2}<\sin^{-1}x+\sin^{-1}y\leq\pi \;\&\;-\dfrac{\pi}{2}\leq\sin^{-1}x,\;\sin^{-1}y\leq\dfrac{\pi}{2}\\ \implies 0<\sin^{-1}x,\sin^{-1}y\leq\dfrac{\pi}{2}\implies 0< x,y\leq1 $$ Case 3-: $-\pi\leq\sin^{-1}x+\sin^{-1}y<-\dfrac{\pi}{2}$

$$ \sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)=-\pi-(\sin^{-1}x+\sin^{-1}y)\\ \implies \color{darkblue}{\sin^{-1}x+\sin^{-1}y=-\pi-\sin^{-1}\Big(x\sqrt{1-y^2}+y\sqrt{1-x^2}\Big)} $$ $$ -\pi\leq\sin^{-1}x+\sin^{-1}y<-\dfrac{\pi}{2} \;\&\;-\dfrac{\pi}{2}\leq\sin^{-1}x,\;\sin^{-1}y\leq\dfrac{\pi}{2}\\ \implies -\dfrac{\pi}{2}\leq\sin^{-1}x,\sin^{-1}y< 0\implies -1\leq x,y< 0 $$

Konstantin
  • 7
Sooraj S
  • 7,573
2

Hope the graph explains the x,y domain ( |x|< 1, |y|< 1 ) and range.

Arcsinx,..&y

Narasimham
  • 40,495
2

Take the sine of both sides, and use the angle addition formula, then further simplify it by using the fact that $\cos\arcsin t=\sqrt{\cos^2\arcsin t}=\sqrt{1-\sin^2\arcsin t}=\sqrt{1-t^2}$. Then apply the $\arcsin$ function to both sides, and you're done.

Lucian
  • 48,334
  • 2
  • 83
  • 154
  • As I have said in my question, I don't have any problem in getting the main part: $ \arcsin(x\sqrt{1-x^2} + y\sqrt{1-y^2}) $. I don't know how to do the range checking so that I can adjust the RHS with $\pi$. – Parth Thakkar Feb 12 '14 at 11:38
  • 1
    @ParthThakkar: $\sin t=\sin(\pi-t)$. (Always picture the unit circle in your mind). And since $\pi$ and $-\pi$ are the same (again, visualize), QED. – Lucian Feb 12 '14 at 17:57