Rewrite $\cos^{-1}x$ in terms of $\sin^{-1}(\sqrt{1-x^2})$

Question

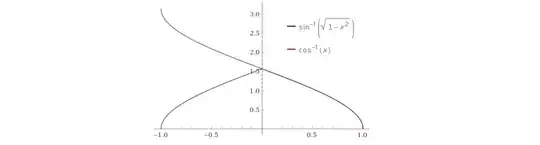
$\cos^{-1}x$, now here $x\in [-1,1]$, we have a requirement to rewrite $\cos^{-1}x$ in terms of $\sin^{-1}$

If $x\ge0$, $\cos^{-1}x$ will give value in the range $\left[0,\dfrac{\pi}{2}\right]$, so $\sin^{-1}\sqrt{1-x^2}$ seems to be correct as this will also give value in the range $\left[0,\dfrac{\pi}{2}\right]$

But if $x<0$, $\cos^{-1}x$ will give value in the range $\left(\dfrac{\pi}{2},\pi\right]$, so in this case what should be $\sin^{-1}x$, should it be $\sin^{-1}\sqrt{1-x^2}$ or $\sin^{-1}-\sqrt{1-x^2}$ ?

If we go with $\sin^{-1}\sqrt{1-x^2}$, then it will give value in the range of $\left(0,\dfrac{\pi}{2}\right]$ or if we go with $\sin^{-1}-\sqrt{1-x^2}$, it will give in the range $\left[-\dfrac{\pi}{2},0\right)$

Hence if $x<0$, there seems no way we can rewrite $\cos^{-1}x$ in terms of $\sin^{-1}$.

What's the catch here, but in most of the textbooks if you see, while giving proofs or solving problems, $\cos^{-1}x$ is rewritten as $\sin^{-1}\sqrt{1-x^2}$, without any constraints on $x$.

Answer 1

The equality

$$\cos^{-1}x=\sin^{-1}\sqrt{1-x^2}$$

only holds for $x\in [0,1]$. For $x\in [-1,0]$, it becomes, $$\cos^{-1}x=\pi - \sin^{-1}\sqrt{1-x^2}$$

which can be seen from the graph below,

Here is a brief analytic proof. Let $\theta = \cos^{-1}x$ with the range $\theta\in[0,\pi]$. Then,

$$\cos\theta = x\implies \sin\theta = \sqrt{1-x^2}$$

which over $\theta\in[0,\pi]$ has two solutions

$$\theta= \sin^{-1}\sqrt{1-x^2},\>\>\>\>\>\theta= \pi-\sin^{-1}\sqrt{1-x^2}$$

corresponding to $x\in[0,1]$ and $x\in[-1,0]$, respectively.

Answer 2

$$cos^{-1}x = \begin{cases} sin^{-1}\sqrt{1-x^2}, \space x \geq 0\\\\ \pi-sin^{-1}\sqrt{1-x^2} , x < 0\end{cases}$$

This can be proven graphically also as shown:

Answer 3

$$\cos^{-1}x=\dfrac\pi2-\sin^{-1}x=\sin^{-1}1+\sin^{-1}(-x)$$

Using Proof for the formula of sum of arcsine functions $ \arcsin x + \arcsin y $

Set $x=1,y=-x$

$$\sin^{-1}(1)+\sin^{-1}(-x)$$

$$= \arcsin1 + \arcsin(-x) =\begin{cases} \arcsin(\sqrt{1-x^2} ) \;\;;1+x^2 \le 1\iff x=0 \;\text{ or }\; 1+x^2 >1\iff x\ne0, 1(-x)< 0\iff x>0\\ \pi - \arcsin( \sqrt{1-x^2}) \;\;;1+x^2 > 1\iff x\ne0, 0< 1,-x \le 1\iff0>x\ge-1\\ -\pi - \arcsin(\sqrt{1-x^2} ) \;\;;1+x^2 > 1\iff x\ne0, -1< 1,-x \le 0\text{ untenable as }1\not\le0 \end{cases} $$