Find the complete solution set of the equation ${\sin ^{ -1}}( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} ) = \frac{\pi }{4} + {\sin ^{ - 1}}x$ is

Question

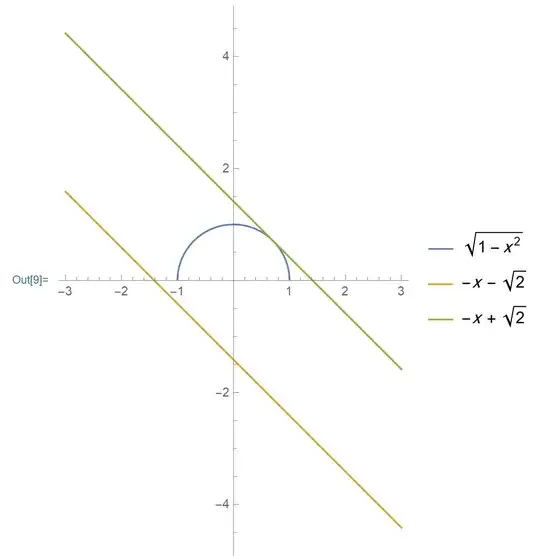
The complete solution set of the equation ${\sin ^{ - 1}}\left( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} \right) = \frac{\pi }{4} + {\sin ^{ - 1}}x$ is

(A)[-1,0]

(B)[0,1]

(C)$[-1,\frac{1}{\sqrt{2}}]$

(D)$[\frac{1}{\sqrt{2}},1]$

My approach is as follow

${\sin ^{ - 1}}\left( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} \right) - {\sin ^{ - 1}}x = \frac{\pi }{4}$

${\sin ^{ - 1}}\left( {\left( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} \right)\sqrt {1 - {x^2}} - x\sqrt {1 - {{\left( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} \right)}^2}} } \right) = \frac{\pi }{4}$

${\sin ^{ - 1}}\left( {\left( {\frac{{x\sqrt {1 - {x^2}} + 1 - {x^2}}}{{\sqrt 2 }}} \right) - x\sqrt {1 - \left( {\frac{{{x^2} + 1 - {x^2} + 2x\sqrt {1 - {x^2}} }}{2}} \right)} } \right) = \frac{\pi }{4}$

${\sin ^{ - 1}}\left( {\left( {\frac{{x\sqrt {1 - {x^2}} + 1 - {x^2}}}{{\sqrt 2 }}} \right) - x\sqrt {\left( {\frac{{2 - 1 - 2x\sqrt {1 - {x^2}} }}{2}} \right)} } \right) = \frac{\pi }{4}$

$\left( {\left( {\frac{{x\sqrt {1 - {x^2}} + 1 - {x^2}}}{{\sqrt 2 }}} \right) - x\sqrt {\left( {\frac{{1 - 2x\sqrt {1 - {x^2}} }}{2}} \right)} } \right) = \frac{1}{{\sqrt 2 }}$

Not able to proceed from here

Answer 1

Substitute $x = \sin\theta$ and let's restrict our attention to $\theta\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ since that covers the whole range of $\sin\theta$:

$$\sin^{-1}\left(\frac{\sin\theta+\cos\theta}{\sqrt{2}}\right) = \frac{\pi}{4}+\sin^{-1}(\sin\theta)$$

$$\implies \sin^{-1}\left(\sin\left(\theta+\frac{\pi}{4}\right)\right) = \frac{\pi}{4}+\theta$$

However, the equality is only true when $$\left|\theta+\frac{\pi}{4}\right|\leq \frac{\pi}{2} \implies -\frac{3\pi}{4}\leq \theta \leq \frac{\pi}{4}$$

Taking the intersection of this set with our original domain, we have that

$$-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{4} \implies -1 \leq x \leq \frac{1}{\sqrt{2}}$$

Answer 2

One way is using differentiation. Let $$f(x) = \sin^{-1}(x) + \frac{\pi}{4}$$ And $$g(x) = {\sin ^{ -1}}( {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} ) $$

---

Edit: Note that domain of $\sin^{-1} x$ is $-1\le x \le 1$. The domain of $f(x) - g(x)$ is $A = \{x | x \in \mathbb{R}, x \in D_f \cap D_g \}$. So we have $$D_f = \{x | x \in \mathbb{R}, -1\le x \le 1\}$$And $$D_g = \{x | x \in \mathbb{R}, -1\le {\frac{{x + \sqrt {1 - {x^2}} }}{{\sqrt 2 }}} \le 1\}$$ If we show $x \in D_f \implies x \in D_g$ then we are done. Because it shows $D_f \subseteq D_g$ and then $D_f \cap D_g = D_f$. Consider $y = x + \sqrt {1 - {x^2}}$ on the interval $x \in [-1 , 1]$. It's a continuous function and $y(-1) =-1, \ \ y(1) = 1$. Taking derivative and finding critical points $$y'(x) = 1 - \frac{x}{\sqrt{1-x^2}} = 0 \implies x = \pm \frac{1}{\sqrt{2}}$$Because $y(\frac{1}{\sqrt{2}}) = \sqrt{2}$ and $y(-\frac{1}{\sqrt{2}}) = 0$ we have $$-1 \le x + \sqrt {1 - {x^2}} \le \sqrt{2} \implies \frac{-1}{\sqrt{2}} \le \frac{x + \sqrt {1 - {x^2}}}{\sqrt{2}} \le 1 $$ Since $-1 \le \frac{-1}{\sqrt{2}}$ the result is proved. This is a geometric interpretation for the mentioned inequity:

---

If $-1\lt x \lt 1$ then $$f'(x) -g'(x) = \frac{1}{\sqrt{1-x^2}} - \frac{\sqrt{1 - x^2} - x}{\sqrt{1 - 2x\sqrt{1 - x^2}} \sqrt{1 - x^2}} $$ Solve for $f'(x) - g'(x) = 0$: $$\sqrt{1 - 2x\sqrt{1 - x^2}} = \sqrt{1 - x^2} - x $$ If $\sqrt{1 - x^2} - x \ge 0$ we can safely square both sides: $$1 - 2x\sqrt{1 - x^2} = 1 - x^2 + x^2 - 2x\sqrt{1 - x^2} $$ Which is an identity. So if $-1\lt x \lt 1$ and $\sqrt{1 - x^2} - x \ge 0$ then $f'(x)- g'(x) = 0$. Therefore we have $f(x) = g(x) + C$. Also $f(0) = g(0) = \frac{\pi}{4}$ concluding $C = 0$. So we have to check the interval $$-1\lt x \lt 1 \ \ \ \text{and} \ \ \ \sqrt{1 - x^2} - x \ge 0$$ Which is $-1 \lt x \le \frac{1}{\sqrt{2}}$. You can easily check $x = -1$ by hand.

Answer 3

The other answers pointed out some very creative ways of solving your problem, but I just wanted to complete your algebraic manipulation for you.

$\left( {\left( {\frac{{x\sqrt {1 - {x^2}} + 1 - {x^2}}}{{\sqrt 2 }}} \right) - x\sqrt {\left( {\frac{{1 - 2x\sqrt {1 - {x^2}} }}{2}} \right)} } \right) = \frac{1}{{\sqrt 2 }}$

${x\sqrt {1 - {x^2}} + 1 - {x^2} - x\sqrt {\left( {1 - 2x\sqrt {1 - {x^2}}} \right)} } = 1$

${x\sqrt {1 - {x^2}} - x\sqrt {\left( {1 - 2x\sqrt {1 - {x^2}}} \right)} } = x^2$

${\sqrt {1 - {x^2}} - \sqrt {\left( {1 - 2x\sqrt {1 - {x^2}}} \right)} } = x$

(Since we divide both sides by $x$, you can verify by hand that $x = 0$ is a solution)

${\sqrt {1 - {x^2}} - \sqrt {\left( {x - \sqrt{1 - {x^2}}} \right)^2} } = x$

${\sqrt {1 - {x^2}} - x + \sqrt{1 - {x^2}}} = x$

$2\sqrt {1 - {x^2}} = 2x$

$\sqrt {1 - {x^2}} = x$

$1 - {x^2} = x^2$

$x^2 = \frac{1}{2}$

$x = \pm \frac{1}{\sqrt{2}}$

Thus, we are left with three solutions: $\{ -\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\}$

Only option choice (C) contains all three solutions found.

Answer 4

First of all we need $-1\le x\le1$ for real $\arcsin(x)$

Using Proof for the formula of sum of arcsine functions $ \arcsin x + \arcsin y $

the equality will be valid

if $$x^2+\dfrac12\le1\iff x^2\le1-\dfrac12\iff?\le x\le?$$

Or if $x^2+\dfrac12>1$ and $(\sqrt2x<0\iff x<0)$