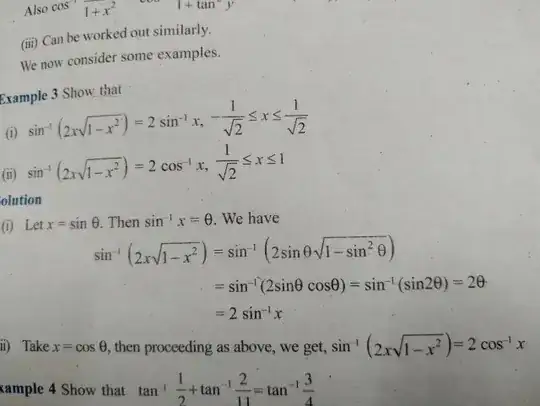There are two similar questions in NCERT Mathematics class 12th book, about Trigonometric inverses but with different domains.
First part of the question asks, show that
$$\sin^{-1} (2x \sqrt{1 - x^2}) = 2\sin^{-1}(x)$$
For $-\frac{1}{\sqrt2} \le x\le \frac1 {\sqrt{2}}$. The solution given substitutes $\sin \theta = x$.
The next part has the same $\text{LHS}$ but has $2\cos^{-1}(x)$ in the $\text{RHS}$ for $\frac1{\sqrt2}\le x\le1$. The solution given substitutes $\cos\theta=x$.
My question is, How do I know when I can substitute what in questions like this? Can't I substitute cos theta and sin theta both for x as given domain is a subset of domain of cos and sin which is $[-1,1]$?
Thank you.