0

The expression $\sin^{-1} (3x-4x^3)$ is equal to $3\sin^{-1} x$ according to this proof: $$\sin^{-1} x = \theta \implies \sin\theta =x....eq.(1)$$ $$\sin 3\theta = 3\sin\theta - 4\sin^3 \theta.....eq.(2)$$ $$\text{Substituting equation 1 into 2 we get...} \sin 3\theta=3x-4x^3$$ $$\therefore 3\sin^{-1} x =\sin^{-1} (3x-4x^3)$$ However, the graphs of both the expressions differ,
The graph of $\sin^{-1} (3x-4x^3)$ is...graph of <span class=$\sin^{-1} (3x-4x^3)$ ">

and the graph of $3\sin^{-1} x$ is ...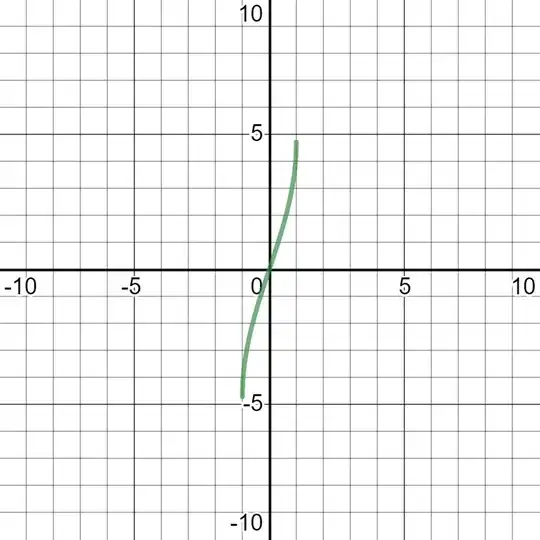

Now my question is

Why do they differ when they are proven to be the same? Is there anything wrong with my proof?

rash
  • 2,060
  • 1
  • 9
  • 28

3 Answers3

2

It works only if $-\pi/6\le \theta\le\pi/6$ or $-\frac{1}{2}\le x\le\frac{1}{2}$

Reason:

As you assumed $\sin\theta = x$,

Now, $\sin 3\theta = 3\sin\theta - 4\sin^3\theta$

$\sin^{-1}(\sin\alpha) =\alpha \iff -\pi/2\le\alpha\le\pi/2$

So, $\sin^{-1}\left(\sin(3\theta)\right) = 3\theta \iff -\pi/2\le3\theta\le\pi/2$

$-\pi/6\le\theta\le\pi/6 \implies -1/2\le\ x \le 1/2$

So,

$$3\sin^{-1}x = \sin^{-1}(3x-4x^3) \iff -1/2\le\ x \le 1/2$$

And you can find the graphs to match exactly in this region

KM101
  • 7,176
19aksh
  • 12,768
2

Note that the range of $\arcsin(y)$ is from $[-\frac{\pi}{2},\frac{\pi}{2}]$ thus for $3\arcsin(x)$ the max value which $\arcsin(x)$ can take is $\frac{\pm\pi}{6}$ so $x\in[-\frac{1}{2},\frac{1}{2}]$.For $\arcsin(3x-4x^3)$ it can take any value between $[-1,1]$Thus the two curves overlap only for $x\in [-\frac{1}{2},\frac{1}{2}]$

Archis Welankar
  • 15,910
2

When working with inverse trig functions, you have to worry (and I mean, really worry) about the domains. Usually the domain given for $\sin \theta $ is restricted to $-\pi/2 \leq \theta \leq \pi/2.$ And this makes the domain for $\sin^{-1} x$ into $-1 \leq x \leq 1.$ As soon as your expression $3x-4x^3$ leaves that domain, you've jumped to a different branch of $\sin^{-1}$.

B. Goddard
  • 1