Why it's true? $\arcsin(x) +\arccos(x) = \frac{\pi}{2}$

Question

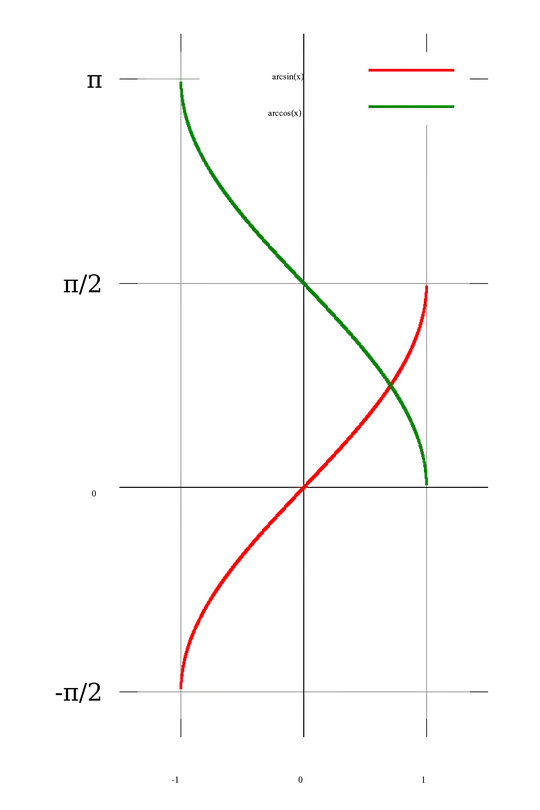
The following identity is true for any given $x \in [-1,1]$: $$\arcsin(x) + \arccos(x) = \frac{\pi}{2}$$

But I don't know how to explain it.
I understand that the derivative of the equation is a truth clause, but why would the following be true, intuitively?

$$\int^{x}_{C1}\frac{1\cdot dx}{\sqrt{1-x^{2}}} + \int^{x}_{C2}\frac{-1 \cdot dx}{\sqrt{1-x^{2}}} =\\ \arcsin(x) - \arcsin(C1) + \arccos(x) - \arccos(C2) = 0 \\ \text{while } \arcsin(C1) + \arccos(C2) = \frac{\pi}{2}$$

I can't find the right words to explain why this is true?

---

Edit #1 (25 Jan, 20:10 UTC):
The following is a truth clause: $$ \begin{array}{ll} \frac{d}{dx}(\arcsin(x) + \arccos(x)) = \frac{d}{dx}\frac{\pi}{2} \\ \\ \frac{1}{\sqrt{1-x^{2}}} + \frac{-1}{\sqrt{1-x^{2}}} = 0 \end{array} $$

By integrating the last equation, using the limits $k$ (a constant) and $x$ (variable), I get the following:

$$ \begin{array}{ll} \int^x_k\frac{1}{\sqrt{1-x^{2}}}dx + \int^x_k\frac{-1}{\sqrt{1-x^{2}}}dx = \int^x_k0 \\ \\ \arcsin(x) - \arcsin(k) + \arccos(x) - \arccos(k) = m \text{ (m is a constant)}\\ \\ \arcsin(x) + \arccos(x) = m + \arcsin(k) + \arccos(k) \\ \\ \text{Assuming that } A = m + \arcsin(k) + \arccos(k) = \frac{\pi}{2} \text{ ,for } x \in [-1,1] \end{array} $$ Using Calculus, why is that true for every $x \in [-1,1]$?

---

Edit #2:

A big mistake of mine was to think that $\int^x_k0 = m \text{ (m is const.)}$, but that isn't true for definite integrals.

Thus the equations from "Edit #1" should be as follows: $$ \begin{array}{ll} \int^x_k\frac{1}{\sqrt{1-x^{2}}}dx + \int^x_k\frac{-1}{\sqrt{1-x^{2}}}dx = \int^x_k0 \\ \\ \arcsin(x) - \arcsin(k) + \arccos(x) - \arccos(k) = 0\\ \\ \arcsin(x) + \arccos(x) = \arcsin(k) + \arccos(k) \\ \\ A = \arcsin(k) + \arccos(k) = \frac{\pi}{2} \text{ ,for } x \in [-1,1] \end{array} $$

Answer 1

There are a couple of ways to see this. Firstly, draw a right triangle, call it $ABC$ (with $C$ being the right angle), with side lengths $a$, $b$ and $c$ with the usual convention. Then $\arcsin(\frac{b}{c})$ is the measure of the angle $CBA$. Additionally, $\arccos(\frac{b}{c})$ is the angle of the angle of the opposite angle $CAB$, so $\arccos(\frac{b}{c}) = \frac{\pi}{2}-\arcsin(\frac{b}{c})$ since the opposite angles must sum to $\frac{\pi}{2}$. From here, you get the result.

We could also do some calculus to figure it out. Let's let $f(x) = \arcsin(x)+\arccos(x)$. Then $f'(x) = \frac{1}{\sqrt{1-x^2}} - \frac{1}{\sqrt{1-x^2}} = 0$. Thus $f$ is constant. What is $f(0)$ equal to?

Answer 2

More simple.... From $\cos \alpha=\sin \left(\dfrac{\pi}{2}-\alpha\right)$ we have: $$ \cos y=x \Rightarrow \sin\left(\dfrac{\pi}{2}-y\right)=x \Rightarrow $$ $$ \Rightarrow \begin{cases} \arccos x=y \\ \arcsin x= \dfrac{\pi}{2}-y \end{cases} \Rightarrow $$ $$ \Rightarrow \arccos x+\arcsin x=\dfrac{\pi}{2} $$

Answer 3

It is pretty obvious to see that $\sin$ and $\cos$ are the same curve, just shifted by $\pi/2$, so if you consider following craphis, it should be clear:

Answer 4

By definition, $\arcsin(x)$ is the angle $\alpha$ such that $\sin(\alpha) = x$ and $-\pi/2 \le \alpha \le \pi/2$, while $\arccos(x)$ is the angle $\beta$ such that $\cos(\beta) = x$ and $0 \le \beta \le \pi$. Since $-\pi/2 \le \alpha \le \pi/2$, $\cos(\alpha) \ge 0$, so we have $\cos(\alpha) = \sqrt{1 - x^2}$. Similarly $\sin(\beta) = \sqrt{1-x^2}$. Now $$\eqalign{-\pi/2 &\le \arcsin(x) + \arccos(x) = \alpha + \beta \le 3 \pi/2 \cr\sin(\alpha + \beta) &= \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) = x^2 + 1 - x^2 = 1\cr \cos(\alpha + \beta) &= \cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta) = \sqrt{1-x^2} x - x \sqrt{1-x^2} = 0}$$ and the only angle in this interval with that sine and cosine is $\pi/2$.

Answer 5

You seem to be starting with the observation that $$ \frac{1}{\sqrt{1-x^2}}+\frac{-1}{\sqrt{1-x^2}}=0 $$ which has the consequence that, for any $c_1,c_2\in[-1,1]$, $$ \int_{c_1}^{x}\frac{1}{\sqrt{1-x^2}}\,dx+\int_{c_2}^{x}\frac{-1}{\sqrt{1-x^2}}\,dx $$ is constant, but not necessarily $0$.

Indeed \begin{multline} \int_{c_1}^{x}\frac{1}{\sqrt{1-x^2}}\,dx+\int_{c_2}^{x}\frac{-1}{\sqrt{1-x^2}}\,dx =\\ \int_{c_1}^{x}\frac{1}{\sqrt{1-x^2}}\,dx+ \int_{c_2}^{c_1}\frac{-1}{\sqrt{1-x^2}}\,dx+ \int_{c_1}^{x}\frac{-1}{\sqrt{1-x^2}}\,dx \end{multline} and this sum is just $$ \int_{c_1}^{c_2}\frac{1}{\sqrt{1-x^2}}\,dx=\arcsin c_2-\arcsin c_1 $$

So the sum of the integrals you're computing is zero only if $c_1=c_2$.

The fact that $\arcsin x+\arccos x=\pi/2$ follows from differentiating: the function $f(x)=\arcsin x+\arccos x$ has zero derivative on $(-1,1)$, so it's constant in that interval and, being continuous on $[-1,1]$ it is constant also in $[-1,1]$. The constant can be evaluated as $$ f(0)=\arcsin 0+\arccos0=0+\frac{\pi}{2}=\frac{\pi}{2}. $$

Answer 6

Write $\theta = \arcsin x$. By definition, this means: $$\sin \theta = x, \qquad -\pi/2 \leq \theta \leq \pi/2.$$

You want to show that $\pi/2 - \theta = \arccos x$. By definition, this means: $$\cos(\pi/2 - \theta) = x, \qquad 0 \leq \pi/2 - \theta \leq \pi.$$

The last inequality follows immediately from the bounds for $\theta$. Furthermore, we have $\cos(\pi/2 - \theta) = \sin \theta = x$ by the complementary angle formula.

Note: To prove the complementary angle formula $\cos(\pi/2 - \theta) = \sin \theta$ in general, an argument with a triangle is not enough, since it will only be valid for acute angles. It is preferable to consider the effect of the reflection through the line $y = x$ on points of the unit circle.

In this figure taken from Trigonometrija by Gel'fand, L'vovskij and Toom, the vertex $B = ?$ of the shaded triangle that is on the circle is the reflection through the diagonal (not shown) of the point $A$ with angular coordinate $x$. The angular coordinate of $B$ is $\pi/2 - x$, so $B = (\cos(\pi/2-x),\sin(\pi/2-x))$. We also have $A = (\cos x,\sin x)$. On the other hand, this reflection takes a point with coordinates $(a,b)$ to the one with coordinates $(b,a)$. Thus $B=(\sin x, \cos x)$, proving that $\cos(\pi/2 - x) = \sin x$. This argument is valid even if $x$ isn't in the first quadrant.

Answer 7

how about using unit circle?

first let us deal with the the first quadrant. we will pick two points $A = (x,y), B = (y,x)$ on the unit circle in the first quadrant. the two points are images of each other on the mirror along the line $y = x$ let us also label the points $P = (1,0), Q = (0,1)$

we will need the following two things:

(a) $arc PA = arc QB,$

(b) $arc PB + arc PA = \pi/2.$

let us use the definition, you can see why the name is apt,
$\arcsin y = \arccos x = arc PA$ where $A = (x, y)$ is a point on the unit circle.

using the above definition $$\arccos x = arc AP, \arcsin x = arc BP, \arccos x + \arcsin x = arc AP + arc BP = \pi/2 $$

the range of $\arccos$ is $[0, \pi]$ and of $\arcsin$ is $[-\pi/2, \pi/2]$. so that when you have negative argument for $arccos$ the point in the second quadrant, and for $\arcsin$ is in the fourth quadrant. the same argument works when $x< 0.$

Answer 8

Why is it true that $\arcsin \theta+\arccos\theta=\frac{\pi}{2}$?

It's actually very simple if you take a geometric approach, which was given by @CameronWilliams in his answer. Here, I just wanted to visualize it:

$$\arcsin\frac{a}{b}=\alpha\because\sin\alpha=\frac{a}{b}$$ $$\arccos\frac{a}{b}=\beta\because\cos\beta=\frac{a}{b}$$

Since $\alpha$ and $\beta$ are complementary angles, angles that add to $\frac{\pi}{2}$ radians, we find that for any ratio of $a $ and $ b$ such that $\frac ab \in [-1,1]$ (from the fact that $\arcsin\theta$ and $\arccos\theta$ are defined for such interval), the sum is always $\frac{\pi}{2}$ radians.