Solving Inverse trig problems using substitution?

Question

I have this problem

$$\arccos\left(\frac{x+\sqrt{1-x^2}}{\sqrt{2}}\right)$$

The answer comes out be $\arcsin(x)-\frac{\pi}{4}$

I've realized that this problem can be solved by using something called substitution, but i really dont get the idea of how you can just substitute $x$ with $\cos(x),~\sin(x)$. Or anything else for that matter.

Also how do you know what to substitute? Is there a method for that?

This has been confusing me a lot and i would appreciate if the answer is not just the solution but also an explanation to how substitution works in brief.

Thanks in advance.

Answer 1

The solution has been discussed so I'll just try to address your other concerns.

The expression to be simplified contains certain suggestions to the substitution. The $x$ and $\sqrt{1-x^2}$ have a sum of squares of 1. This is reminiscent of either the $\sin x$ function or $ \cos x$ functions. So we try to substitute say, $x=\sin\alpha$.

With inverse trigonometric expressions however this gets a little tricky.

1. You have to ensure that your substitution satisfies the domain. For example, here plugging $x=\sin\alpha$ would be invalid if $x$ could take all real values because the range of $\sin x$ is $[-1,1]$. We can do that here because $\sqrt{1-x^2}$ requires $\mid x\mid <1$ .

2. $\mathrm{sin}\alpha$ is a many-one function. In fact for any $\alpha$ you take $n\pi +(-1)^n\alpha$ gives the same value. So if your simplified expression contains $\alpha$ you would get an infinite number of values for the resultant function . But the $\mathrm{arccos}$ function is single valued. So we have to restrict the domain of $\alpha$ to ensure that $\sin\alpha$ takes all values of $x$ and that each $x$ corresponds to a single $\alpha$.(Establish a bijection between $x$ and $\alpha$ so to speak)

3. The easiest way to do this usually is to assume $\alpha =\sin^{-1}(x)$ this forces $\alpha\in [-\tfrac{\pi}{2},\tfrac{\pi}{2}]$.

Another note other people missed on is that $\sqrt{1-sin^2\alpha}$ is $\mid\cos\alpha\mid$. It is only when you consider our restriction on $\alpha$ that you can justify that $ \cos\alpha$ is positive in $\in [-\tfrac{\pi}{2},\tfrac{\pi}{2}]$.

Finally, for inverse trig functions, while: $$\mathrm{trig}(\mathrm{trig}^{-1}x)=x$$ Is true but: $$\mathrm{trig}^{-1}(\mathrm{trig}(x))=x$$ This is true only when $x$ lies in the Principal value branch of $\mathrm{trig}$(Denotes any of the six functions.

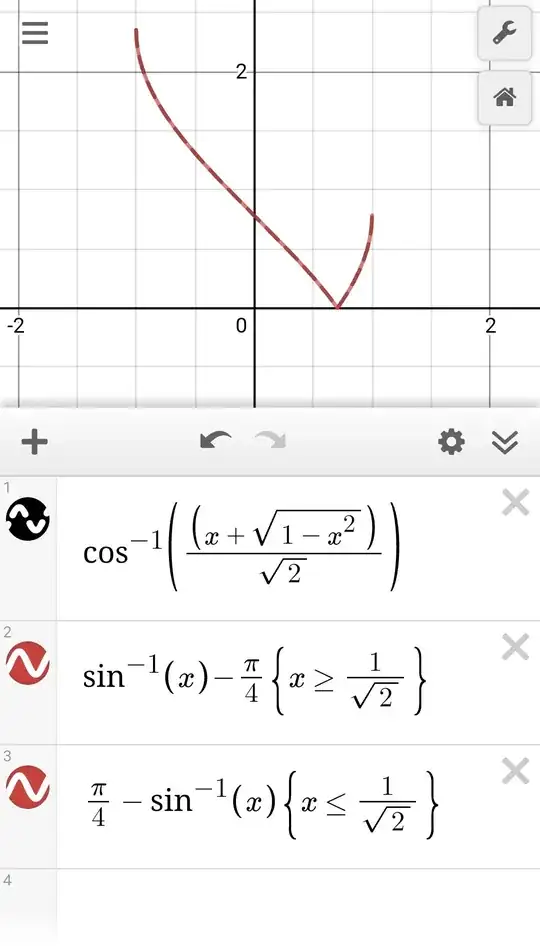
So, once you have simplified the function to: $\cos^{-1}(\cos(\alpha-\tfrac{\pi}{4}))$ You have to look at what your value of $\alpha$ is before you cancel cos inverse and cos.

Look up the graph for $\cos^{-1}(\cos x)$ and you'll notice that: $$\cos^{-1}(\cos x)= x ;0\leq x\leq \pi$$ $$\cos^{-1}(\cos x)= -x ;-\pi\leq x\leq 0$$

So,

$$\cos^{-1}(\cos (\alpha-\tfrac{\pi}{4}))= \alpha-\tfrac{\pi}{4};\tfrac{\pi}{4}\leq \alpha\leq \tfrac{5\pi}{4}$$ $$\cos^{-1}(\cos (\alpha-\tfrac{\pi}{4}))= \tfrac{\pi}{4}-\alpha ; -\tfrac{3\pi}{4}\pi\leq \alpha\leq \tfrac{\pi}{4}$$

Checking the appropriate ranges on $x$ corresponding to $\alpha$ gives $x\geq \tfrac{1}{\sqrt{2}}$ and $x\leq \tfrac{1}{\sqrt{2}}$ for the first and second case respectively.

Finally a note on choosing substitutions. You should try to find the substitution that has an identity most closely resembling the given expressions.

Examples:(Try to simplify the expressions and identify the corresponding identity.)

1. $x, \sqrt{x^2-a^2}$ , use $x=a\sec\alpha$ or $\csc\alpha$.
2. $x, \sqrt{a^2+x^2}$, use $x=a\tan\alpha$
3. $\sqrt{1-x},\sqrt{1+x}$, use $x=a\cos2\alpha$
4. $\sqrt{a-x}{x-b}, \sqrt{\dfrac{a-x}{x-b}}$ use $x=a\sin^2\theta +b\cos^2 \theta$. (Slightly esoteric, rare use)

Answer 2

I assume you want to simplify the expression.

---

$\sqrt{1-x^2}$ is defined only when $|x|\leq 1$. Hence, if we let $x=\sin \alpha$, note that for every possible value of $x$ we can select a value of $\alpha$.

Let $t=\arccos\left( \dfrac{x+\sqrt{1-x^2}}{\sqrt 2}\right)$.

Now, $$t=\arccos \left(\dfrac{\sin \alpha + \cos \alpha}{\sqrt 2}\right)$$ Or $$t=\arccos \left(\cos (\alpha-\pi/4)\right)=\alpha -\pi/4$$ This gives us $t=\arcsin x -\pi/4$.

Note: the above is valid only for certain values of $\alpha$. I have left this for you as an exercise(the values for which it is valid).

Edit:

$ t = \begin{cases} \arcsin x-\pi/4, & 1\geq x\geq 1/\sqrt 2 \\ \pi/4 -\arcsin x, & 1/\sqrt 2\geq x\geq -1 \end{cases}$

Corresponding Desmos plot:

Answer 3

We need to be very careful about the ranges while dealing with Inverse Trigonometric Functions(Statement)

Let $\arccos x=u\implies0\le u\le\pi,$

$x=\cos u,\sin u=+\sqrt{1-x^2}$

$$f(x)=\arccos\left(\dfrac{\cos u+\sin u}{\sqrt2}\right)=\arccos\left(\cos\left(u-\dfrac\pi4\right)\right)$$

Now $-\dfrac\pi4\le u-\dfrac\pi4\le\pi-\dfrac\pi4$

So if $u-\dfrac\pi4\ge0\iff x=\cos u\le\cos\dfrac\pi4=?,$

$$f(x)=u-\dfrac\pi4$$

If $u-\dfrac\pi4<0\iff x=\cos u>\cos\dfrac\pi4=?,$

$$f(x)=-\left(u-\dfrac\pi4\right)$$

Now use Why it's true? $\arcsin(x) +\arccos(x) = \frac{\pi}{2}$