Two differentiation results of $\sin^{-1}(2x\sqrt{1-x^2})$

Question

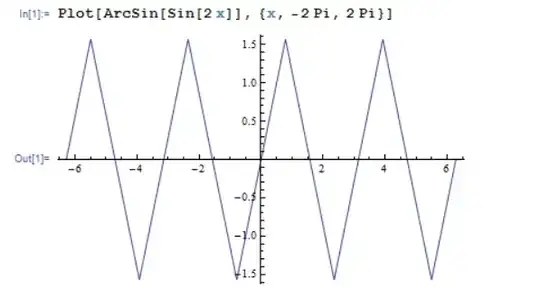
While trying to differentiate $\sin^{-1}(2x\sqrt{1-x^2})$, if we put $x = \sin\theta$, we get,

\begin{align*} y &=\sin^{-1}(2x\sqrt{1-x^2})\\ &= \sin^{-1}(2\sin\theta\sqrt{1-\sin^2\theta})\\ &= \sin^{-1}(2\sin\theta\cos\theta)\\ &= \sin^{-1}(\sin2\theta)\\ &= 2\theta\\ &= 2\sin^{-1}x. \end{align*}

So, \begin{align*} \frac{dy}{dx} &= \frac{2}{\sqrt{1-x^2}}.\\ \end{align*}

But if we put $x = \cos\theta$, we get,

\begin{align*} y &=\sin^{-1}(2x\sqrt{1-x^2})\\ &= \sin^{-1}(2\cos\theta\sqrt{1-\cos^2\theta})\\ &= \sin^{-1}(2\cos\theta\sin\theta)\\ &= \sin^{-1}(\sin2\theta)\\ &= 2\theta\\ &= 2\cos^{-1}x. \end{align*}

This time,

\begin{align*} \frac{dy}{dx} &= -\frac{2}{\sqrt{1-x^2}}.\\ \end{align*}

We are perplexed about the difference in sign between the two results and thought that you could help.

(We understand that we can differentiate $\sin^{-1}(2x\sqrt{1-x^2})$ directly, without any substitution, which gives us the first result.)

Answer 1

Remember that $\sin^{-1}$ is not a "true inverse". Here is a graph of $\sin^{-1}(\sin(2x))$.

I think it is clear that this is the most likely source for your sign error. As you note, you could have a different choice for arcsin which would give you the opposite sign when differentiating.

I think the easiest way to reason into the first choice is that because $\sin^{-1}(x)$ is increasing your derivative should be positive.

If you wanted to be more precise, remember that you are only considering values of $x$ such that $-1 \leq 2x\sqrt{1-x^2} \leq 1$. If you let $x = \cos\theta$ you will use values of theta that are greater than $\pi/2$ because you need $x$ to be negative. If you let $x = \sin(\theta)$ you can let $\theta$ take on values between $-\pi/2$ and $\pi/2$ which is where $\sin^{-1}$ is "nicely defined".

After all of this, let me correct an error in your work. This is where the "paradox" arises.

For $x = \sin(\theta)$

\begin{align*} y &=\sin^{-1}(2x\sqrt{1-x^2})\\ &= \sin^{-1}(2\sin\theta\sqrt{1-\sin^2\theta})\\ &= \color{red}{\sin^{-1}(2\sin\theta|\cos\theta|)}\\ \end{align*}

For $x = \cos\theta$

\begin{align*} y &=\sin^{-1}(2x\sqrt{1-x^2})\\ &= \sin^{-1}(2\cos\theta\sqrt{1-\cos^2\theta})\\ &= \color{red}{\sin^{-1}(2\cos\theta|\sin\theta|)}\\ \end{align*}

If we chose $x = \sin(\theta)$ then $\theta$ is such that $\cos(\theta)$ is always positive and we don't need the absolute value signs and we can continue just as we did.

If we choose $x = \cos(\theta)$ then $\theta$ is such that $\sin(\theta)$ is always negative so here is the source of the discrepancy. A negative sign should be introduced after taking the square root.

Answer 2

This Question bugged me for long time before I found the linked identity

Setting $y=x$ in Proof for the formula of sum of arcsine functions $ \arcsin x + \arcsin y $,

$$ 2\arcsin x\\ \begin{align} &=\arcsin( 2x\sqrt{1-x^2}) \;\;;2x^2 \le 1 \\ &=\pi - \arcsin(2x\sqrt{1-x^2}) \;\;;2x^2 > 1\text{ and } 0< x\\ &=-\pi - \arcsin(2x\sqrt{1-x^2}) \;\;;2x^2 > 1\text{ and } x\le 0\\ \end{align} $$

Case $\#1:$ If $2x^2 \le 1,\arcsin( 2x\sqrt{1-x^2})=2\arcsin x$

Case $\#2:$ If $2x^2> 1,$

Case $\#2A: x>0,\arcsin( 2x\sqrt{1-x^2})=\pi-2\arcsin x=2\arccos x$

Case $\#2B: x\le0,\arcsin( 2x\sqrt{1-x^2})=-\pi-2\arcsin x$