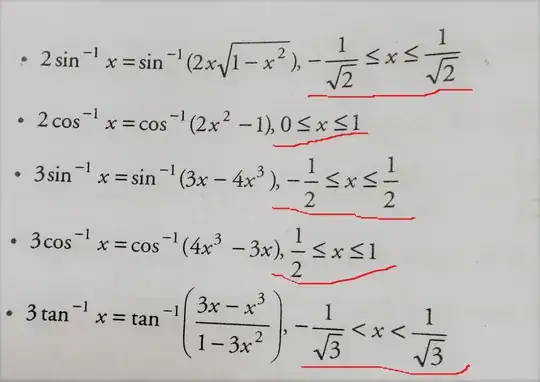How do you find the domain of the function $y=\arcsin\left({2x\sqrt{1-x^{2}}}\right)$
I know that the domain of $\arcsin$ function is $[-1,1]$
So, $-1\le{2x\sqrt{1-x^{2}}}\le1$ probably?
or maybe $0\le{2x\sqrt{1-x^{2}}}\le1$ , since $\sqrt{1-x^{2}}\ge0$ ?
EDIT: So many people have answered that the domain would be $[-1,1]$ but my book says that its $[\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}}].$ 
Can anyone explain how are those restrictions made in the given formulas?
You should see the domain is at first restricted by the square root $\sqrt{1-x^2}$ so that we must have $|x|\le 1$. Also note that $g(x) = 2x\sqrt{1-x^2}$ is an odd function, so we can just analyse for $x> 0$.
$$g'(x) = 2 \sqrt{1-x^2} -\frac{2x^2}{\sqrt{1-x^2}} = \frac{2-4x^2}{\sqrt{1-x^2}}$$
Giving maxima at $x = \tfrac{1}{\sqrt{2}}$. So $g(\tfrac{1}{\sqrt{2}}) = 1$ and $g(0) = 0$. So we have shown that $0 \le g(x) \le 1$ for $x \in [0,1]$. Similarly we show $0 \ge g(x) \ge -1$ for $x \in [-1,0]$
So required domain is $[-1,1]$
In order to compute $\arcsin(2x\sqrt{1-x^2})$, you need that $$ \bigl|2x\sqrt{1-x^2}\,\bigr|\le 1 $$ which becomes $$ 4x^2(1-x^2)\le 1 $$ and therefore $$ 4x^4-4x^2+1\ge0 $$ Since the left-hand side is a square, the inequality is satisfied for every $x$, provided $1-x^2\le1$. This is equivalent to $-1\le x\le 1$.
You are misreading the assignment, which asks you to prove that, for $|x|\le1/\sqrt{2}$, you have $$ 2\arcsin x=\arcsin\bigl(2x\sqrt{1-x^2}\,\bigr) $$ Note that this doesn't hold, for instance, when $x=1$, because the left-hand side is $\pi$, whereas the right-hand side is $0$.
Set $\alpha=\arcsin x$. Since we're assuming $|x|\le 1/\sqrt{2}$, we have $-\pi/4\le\alpha\le\pi/4$. Therefore $\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-x^2}$. Then $$ 2x\sqrt{1-x^2}=2\sin\alpha\cos\alpha=\sin2\alpha $$ Since $-\pi/2\le 2\alpha\le \pi/2$, we have $$ \arcsin\bigl(2x\sqrt{1-x^2}\,\bigr)= \arcsin\sin2\alpha=2\alpha=2\arcsin x $$ as required. The other questions are similar.
With more advanced tools. Let $f(x)=\arcsin\bigl(2x\sqrt{1-x^2}\,\bigr)$. Then $$ f'(x)=\frac{1}{\sqrt{1-4x^2(1-x^2)}} \left(2\sqrt{1-x^2}+2x\frac{-x}{\sqrt{1-x^2}}\right) =\frac{1}{|1-2x^2|}\frac{2(1-2x^2)}{\sqrt{1-x^2}} $$ This coincides with the derivative of $g(x)=2\arcsin x$ only for $1-2x^2>0$, that is, $-1/\sqrt{2}<x<1/\sqrt{2}$.
Since $f(0)=g(0)$, the two functions are equal only on the interval $[-1/\sqrt{2},1/\sqrt{2}]$ (at the extremes by continuity).
You can also say that $$ \arcsin\bigl(2x\sqrt{1-x^2}\,\bigr)= \begin{cases} c_1-2\arcsin x & -1\le x<-1/\sqrt{2} \\[4px] 2\arcsin x & -1/\sqrt{2}\le x\le 1/\sqrt{2} \\[4px] c_2-2\arcsin x & 1/\sqrt{2}<x\le1 \end{cases} $$ and you can easily determine the constants $c_1$ and $c_2$ by using continuity or by using that $f(-1)=0$ and $f(1)=0$.
or maybe $0\le2x\sqrt{1-x^2}\le1$, since $\sqrt{1-x^2}>0$ ?
You can’t do that. Let $x = -1/2$, then $\sqrt{1-x^2}>0$, but $2x<0$, so arcsine’s argument is negative. (Also, there is a typo: square root is in general nonnegative, not only positive—and in this case, it actually could be zero.)
Also, you should add $1-x^2\ge0$ to the inequalities to solve, as square root’s argument should be nonnegative. This could possibly narrow the domain.
(Similar to lab bhattacharjee hint)
Putting $x=\cos t$ where $t\in[0,\pi]$ this is allowed because $x\in[-1,1]$ (otherwise $\sqrt{1-x^2}$ is not defined) and $\cos$ is bijective from $[0,\pi]\to [-1,1]$. Then we have to find $$y=\arcsin(2\cos t\sqrt{\sin^2 t})$$ When $t\in[0,\pi]$ we have that $\sin t\geq 0$ so $\sqrt{\sin^2 t}=\sin t$ so $$y=\arcsin(2\cos t\sin t)=\arcsin(\sin 2t)$$ Since $-1\leq\sin 2t\leq 1$ this means that $\arcsin(\sin(2t))$ is always defined so the domain of $y$ is $[-1,1]$.
A proof without calculus or trigonometry.
$$\begin{aligned} (1-2x^2)^2&\geq0 \\ (1-4x^2+4x^4)&\geq0 \\ x^2-x^4&\leq\frac{1}{4} \\ 0\leq \sqrt{x^2({1-x^2})}&\leq\frac{1}{2} \\ 0\leq |x\sqrt{1-x^2}|&\leq\frac{1}{2} \\ -1\leq 2x\sqrt{1-x^2}&\leq1 \end{aligned}$$
Then, since $\arcsin:\,[-1,1]\mapsto\left[\frac{-\pi}{2},\frac{\pi}{2}\right]$, the domain is $[-1,1]$.
