274

The approximation $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ was proposed by Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician.

I wondered how much this could be improved using our computers and so I tried (very immodestly) to see if we could do better using $$\sin(x) \simeq \frac{a (\pi -x) x}{5 \pi ^2-b (\pi -x) x}$$ I so computed $$\Phi(a,b)=\int_0^{\pi} \left(\sin (x)-\frac{a (\pi -x) x}{5 \pi ^2-b (\pi -x)x}\right)^2 dx$$ the analytical expression of which not being added to the post. Settings the derivatives equal to $0$ and solving for $a$ and $b$, I arrived to $a=15.9815,b=4.03344$ so close to the original approximation !

What is interesting is to compare the values of $\Phi$ : $2.98 \times 10^{-6}$ only decreased to $2.17 \times 10^{-6}$. Then, no improvement and loss of attractive coefficients.

Now, since this is a matter of etiquette on this site, I ask a simple question:

with all the tools and machines we have in our hands, could any of our community propose something as simple (or almost) for basic trigonometric functions ?

In the discussions, I mentioned one I made (it is probable that I reinvented the wheel) in the same spirit $$\cos(x) \simeq\frac{\pi ^2-4x^2}{\pi ^2+x^2}\qquad (-\frac \pi 2 \leq x\leq\frac \pi 2)$$ which is amazing too !

emacs drives me nuts
  • 10,390
  • 2
  • 12
  • 31
Claude Leibovici
  • 260,315

5 Answers5

150

One simple way to derive this is to come up with a parabola approximation. Just getting the roots correct we have

$$f(x)=x(\pi-x)$$

Then, we need to scale it (to get the heights correct). And we are gonna do that by dividing by another parabola $p(x)$

$$f(x)=\frac{x(\pi-x)}{p(x)}$$

Let's fix this at three points (thus defining a parabola). Easy rational points would be when $\sin$ is $1/2$ or $1$. So we fix it at $x=\pi/6,\pi/2,5\pi/6$.

We want $$f(\pi/6)=f(5\pi/6)=1/2=\frac{5\pi^2/36}{p(\pi/6)}=\frac{5\pi^2/36}{p(5\pi/6)}$$ And we conclude that $p(\pi/6)=p(5\pi/6)=5\pi^2/18$

We do the same at $x=\pi/2$ to conclude that $p(\pi/2)=\pi^2/4$.

The only parabola through those points is

$$p(x)=\frac{1}{16}(5\pi^2-4x(\pi-x))$$

And thus we have the original approximation.

In the spirit of answering the question: This method could be applied for most trig functions on some small symmetric bound.

BeaumontTaz
  • 2,795
  • 2
    @BeaumontTaz. Inspired by your answer, I selected three points at $x=\alpha,\frac{\pi}{2},\pi-\alpha$ from which the coefficients can be computed as functions of $\alpha$. I set $\alpha=\frac{n\pi}{8!}$ to maintain rationality and I searched for $n$ such that the integral in the post be minimum. I found $n=7017$ instead of $n=6720$ (corresponding to $\frac{\pi}{6}$). The value of the integral changed from $2.97776\times 10^{-6}$ to $2.94776\times 10^{-6}$ which is just ridiculous. One more proof of how clever is the choice of $\frac{\pi}{6}$ ! – Claude Leibovici Oct 18 '14 at 05:10
  • 1
    @ClaudeLeibovici, what does the choice of $\alpha=\frac{n\pi}{8!}$ maintain rationality of? – BeaumontTaz Oct 18 '14 at 11:03
  • 2
    @BeaumontTaz. I did not want to have an irrational value for the optimum $\alpha$. That's it ! Cheers :-) – Claude Leibovici Oct 18 '14 at 11:15
  • @ClaudeLeibovici, the next step would probably be to not keep it fixed at $(\pi/2,1)$ and fix it at like $x=\alpha,\beta,\pi-\beta,\pi-\alpha$ and see what we get. – BeaumontTaz Oct 18 '14 at 18:08
  • @BeaumontTaz. Good idea but it will be limited to $x=\alpha,\beta,\pi-\alpha$ since we only have $3$ parameters as a total. I shall look at it. – Claude Leibovici Oct 19 '14 at 03:39
  • @ClaudeLeibovici, unless we fit a cubic to it to the four points we need? – BeaumontTaz Oct 19 '14 at 04:23
  • In such a case, it would be better to use one more term in a continued fraction. By the way, I made with three point. The result is $\alpha=0.546741$, $\beta=1.57080\approx \pi/2$ !! – Claude Leibovici Oct 19 '14 at 04:26
  • 3
    @BeaumontTaz amazing answer. What is the intuition behind scaling of $x(\pi-x)$ by dividing with $p(x)$, and not by some multiplicative function ? – kaka Oct 22 '14 at 19:58
  • 3
    @kaka. My intuition behind dividing by $p(x)$ was that it was the already established form of the approximation. It was using the knowledge that we know what we're going for. Kinda cheating. However, I did just spend some time solving for a $q(x)$ such that $g(x) = q(x)x(\pi-x)$ and it doesn't turn out nearly as appealing, not to mention the fact that it's a fourth order polynomial, now. However, I will mention that it is a more accurate approximation having $\Phi = 1.118\times10^{-6}$. I will post the both $q(x)$ and $g(x)$ in a proceeding comment. – BeaumontTaz Oct 22 '14 at 20:57
  • 2
    @kaka $$q(x) = \frac{36x(\pi-x)+31\pi^2}{10\pi^4}$$ $$g(x)=\frac{36\left[x(\pi-x)\right]^2+31\pi^2\left[x(\pi-x)\right]}{10\pi^4}$$ – BeaumontTaz Oct 22 '14 at 21:00
  • 1
    @kaka I added an answer trying to address your question, in case you were still curious – D.R. Aug 27 '21 at 06:03
55

This might be more explicable if you observe that it is the same thing as

$$ \csc(x) \approx -\frac{1}{4} + \frac{5 \pi}{16} \left( \frac{1}{x} + \frac{1}{\pi - x} \right) $$

The two summands in the parentheses are obvious if you want to get the poles of $\csc$ correct. If you wanted a good approximation of $\csc$ near the poles, then the coefficient out front should be $1$. But since we're approximating $\sin$, it's okay to get that wrong because anything near zero is near zero.

The extreme point is at $\csc(\pi/2) = 1$; in the approximation, this would become

$$ -\frac{1}{4} + \frac{5 \pi}{16} \left( \frac{2}{\pi} + \frac{2}{\pi} \right) = -\frac{1}{4} + \frac{5}{4} = 1$$

and so we see the appearance of the remaining copy of $\pi$ is to cancel out the other two $\pi$'s. All that's left is to tune the factor $\frac{5}{16}$ to something appropriate, and adjust the $-\frac{1}{4}$ to compensate. I'm not sure where the choice of $\frac{5}{16}$ comes from, although it's quite plausible it ought to be near $\frac{1}{\pi}$; maybe it was chosen just to be a small fraction whose denominator was divisible by $4$, so as to cancel the $4$ in $\frac{4}{\pi}$.

As a bit of an aside, my comment about the poles suggests an infinite sum for $\csc(x)$ that I hadn't seen before:

$$ \csc(x) = \sum_{n=-\infty}^{+\infty} (-1)^n \frac{1}{x - \pi n} $$

  • Maybe $ \frac{5}{16} = 0.3125 \approx \frac{\pi}{10} $ ? $ \frac{1}{\pi} \approx 0.3183 $. – jpmc26 Oct 17 '14 at 00:17
  • 1
    @jpmc26, the fractions arise naturally from trying to fit a parabola $p(x)$ to the points $\left(\frac{\pi}{6},\frac{5\pi^2}{18}\right), \left(\frac{\pi}{2},\frac{\pi^2}{4}\right), \left(\frac{5\pi}{6},\frac{5\pi^2}{18}\right)$ which would make $$f(x)=\frac{x(\pi-x)}{p(x)}=\sin{(x)}$$ at $x=\frac{\pi}{6},\frac{\pi}{2},\frac{5\pi}{6}$. I flushed it out a little more in my answer. Also, this wiki page and this answer might help. – BeaumontTaz Oct 17 '14 at 06:32
  • @jpmc26 Also, the slope of our approximation at $x=0$ is $\frac{16}{5\pi}$ and the slope of $\sin$ at $x=0$ is $1$. So basically $\frac{16}{5\pi}\approx 1$ which means that $\frac{16}{5}\approx \pi$ You seem to be right or at least it's a coincidence that $\frac{5}{16}\approx \frac{1}{\pi}$. – BeaumontTaz Oct 17 '14 at 06:40
  • I believe the last sum can be derived as a consequence of the Mittang-Leffler expansion theorem : $f(z)$ be a function with simple poles $a_i$ with residues $b_i$ respectively on $\Bbb C$. Then $$f(z) = f(0) + \sum_{n = 1}^\infty b_n \left [ \frac1{z-a_n} + \frac1{a_n} \right ]$$ – Balarka Sen Oct 17 '14 at 22:33
  • The ratio of two polynomials is called a rational approximation. These are usually much better than plain polynomials because they behave better "at infinity" – Philip Roe Apr 08 '17 at 22:44
46

While you're at it, try also $\cos\bigg(\dfrac\pi2x\bigg)\simeq\Big(1-x^2\Big)^\tfrac65$ and $\cos\bigg(\dfrac\pi2x\bigg)\simeq\Big(1-x^2\Big)^\tfrac76$.

But since the numerical evaluation of fractional powers is significantly more time-

consuming in terms of CPU, we can substantially improve this by using the binomial

series for $\Big(1-x^2\Big)^\tfrac15$, and experimentally adjusting the coefficient, finally arriving at

$\color{seagreen}{\cos\bigg(\dfrac\pi2x\bigg)\simeq\Big(1-x^2\Big)\bigg(1-\dfrac{x^2}{4.5}\bigg)}$, which yields an absolute error of about $\pm1$ ‰

Lucian
  • 48,334
  • 2
  • 83
  • 154
  • 5
    Let me give one : $\cos(x) \approx \frac{5 \pi ^2}{x^2+\pi ^2}-4$. I don't know if it is new or not (I built it in the same spirit as the one for the sine). Is that any good ? ($0\leq x\leq \pi/2$). – Claude Leibovici Oct 16 '14 at 15:02
  • 2
    @ClaudeLeibovici: Probably based on the fact that $\dfrac1{1+x^2}\approx1-x^2$, since $x^4\approx0$. – Lucian Oct 16 '14 at 15:10
  • Except that that formula requires performing fractional exponents, so arguably not simpler. – Daniel R Hicks Oct 16 '14 at 17:35
  • @DanielRHicks: Did I say otherwise? – Lucian Oct 17 '14 at 00:31
  • 1
    @Lucian. Just use $\cos(x) \approx \frac{5 \pi ^2}{x^2+\pi ^2}-4$ and make $x=\frac{\pi y}{2}$ to get $\cos\bigg(\dfrac\pi2 y\bigg)\simeq \frac{4 \left(1-y^2\right)}{y^2+4}$ – Claude Leibovici Oct 17 '14 at 07:19
  • @ClaudeLeibovici: I can't help but suspect a connection to the infinite product formula for $\cos\bigg(\dfrac\pi2~x\bigg)=$ $=\displaystyle\prod_{n~=\tfrac12}^\infty\bigg(1-\frac{x^2}{4n^2}\bigg)$, whose first two terms are $\Big(1-x^2\Big)\bigg(1-\dfrac{x^2}9\bigg)$. – Lucian Aug 17 '15 at 15:36
4

I would like to add an addendum to @BeaumontTaz's wonderful derivation of the approximation, because I think I have a very simple answer to user @kaka's comment "What is the intuition behind scaling of $x(\pi−x)$ by dividing with $p(x)$, and not by some multiplicative function ?". The key prerequisite to this approximation is I think the knowledge of the five nicest/simplest values of the sine function on $[0,\pi]$, namely $\sin(0) = 0, \sin(\frac \pi 6) = \frac 12, \sin(\frac \pi 2) = 1, \sin (\frac{5\pi}6) = \frac 12, \sin (\pi) = 0$. It is no surprise that these values were known to Bhaskara I in the 7th century, as all the values are rational (none of that square-rooty business that apocryphally got someone killed), and can be easily derived through the 30-60-90 triangle.

Anyways, as BeaumontTaz did, the first order of business is to approximate using the zeroes, so $f(x)= x (\pi-x)$. Then obviously, we want $f(\frac \pi 2) = \sin (\frac \pi 2) = 1$, so the easiest thing we could do is scale by $\frac 1{f(\pi/2)}$ and get the approximation $$a_1(x) = \frac{x(\pi-x)}{f(\pi/2)}.$$ This is not too good of an approximation, so we hope to do better. Lucky for us, we still have two pieces of information left! We want our approximation to agree with $\sin x$ at $x = \frac \pi6, \frac{5\pi}6$ as well. So at $x=\frac \pi6$, we would need to scale by $\frac{\sin(\pi/6)}{f(\pi/6)} = \frac{1}{2f(\pi/6)}$, and similarly at $x= \frac{5\pi}6$ we would scale by $\frac{\sin(5\pi/6)}{f(5\pi/6)} = \frac{1}{2f(5\pi/6)}$. In summary, at $x = \frac \pi6, \frac \pi2, \frac{5\pi}6$ respectively, we would like to divide by $2f(\pi/6), f(\pi/2), 2f(5\pi/6)$ respectively, i.e. we have a "scaling function" $s(x)$ that we divide by that we have pinned down at three values, and an approximation $a(x) = \frac{f(x)}{s(x)}$. What's the easiest way to extend a function defined at three points? Well, there is exactly one parabola passing through those three points, and parabolas are very easy to deal with, so let us simply take $s(x)$ to be the parabola passing those three points.

So we see that the reason it is "more natural" to divide by the scaling instead of multiplying like @kaka suggested was because in this problem the first idea we had of scaling was in the form of a division ("priming our mind for division"), and all the scaling factors looked like $\frac{1}{\text{something}}$, and it is easier to deal with/look at interpolation at points $(\frac \pi 6, 2f(\frac \pi 6)), (\frac \pi 2, f(\frac \pi2)), (\frac{5\pi}6, 2f(\frac{5\pi}6))$ than interpolation at points $(\frac \pi 6, \frac{1}{2f(\frac \pi 6)}), (\frac \pi 2, \frac{1}{f(\frac \pi2)}), (\frac{5\pi}6, \frac1{2f(\frac{5\pi}6)})$. Said another way, when we want to "renormalize" $f(\frac \pi 6)$ to $\frac 12$, I think people naturally think "divide by $f(\frac \pi 6)$ to normalize to 1, and then divide by 2/multiply by $\frac 12$ to get to $\frac 12$", i.e. the idea of "normalization to 1" is "more naturally" thought of as a division rather than a multiplication by reciprocal.

I do think aesthetics/simplicity play some role in formulas like these (they were written out in verses in Sanskrit), and the formula for the parabola passing through $(\frac \pi 6, 2f(\frac \pi 6)), (\frac \pi 2, f(\frac \pi2)), (\frac{5\pi}6, 2f(\frac{5\pi}6))$ is much nicer (especially if we write things in terms of degrees instead of radians) than the formula for the parabola passing through $(\frac \pi 6, \frac{1}{2f(\frac \pi 6)}), (\frac \pi 2, \frac{1}{f(\frac \pi2)}), (\frac{5\pi}6, \frac1{2f(\frac{5\pi}6)})$ (taking reciprocals in the latter case messes up things quite a lot). Indeed explicitly writing out the interpolation w.r.t. the first and second set of points in degrees, we have $s_1(x) = \frac{1}{4}x^{2}-45x+10125$ and $s_2(x)=-\frac{1}{291600000}x^{2}+\frac{1}{1620000}x+\frac{31}{324000}$; you can visualize them here: https://www.desmos.com/calculator/aiqcjbbcn2.

I hope this answer gave a little bit more details to the "naturality" of dividing by scaling factors (and the "naturality" of the entire construction/approximation --- basically I argue that the formula in Claude's question is the simplest and most reasonable approximation given exactly the five "trivial" values of $\sin x$), and didn't just repeat what people already knew.

D.R.
  • 8,691
  • 4
  • 22
  • 52
2

I wondered how much this could be improved using our computers

Here is an overview of how much Bhāskara's formula can be improved, given as abolute and relative errors of the respective formulas, and as %-values relative to Bhāskara's approximation.

Approximation of $\cos x$ for $|x|\leqslant\frac\pi2$ Absolute Error Relative Error
Bhāskara I's $(\pi^2-4x^2)/(\pi^2+x^2)$ 0.00163 (100%) 0.019 (100%)
Best degree [2/2] rational function 0.00098 (60%) 0.0047 (25%)
Best degree 4 polynomial 0.0006 (37%) 0.0027 (15%)

The values and functions are worked out in the remainder.

Absolute Error

If we want to minimize the absolute error, it's simpler to start with approximating $\cos$ for $|x|\leqslant \pi/2$. We start by approximating

$$ f(x) = \cos(\sqrt x) \quad \text{ with }\quad x\in[0,\pi^2/4] \tag 1$$ and then use $$ \cos x = f(x^2) \tag2 $$ That way, we get the symmetry of $\cos$ and $f$ can be approximated by a rational function $g$ of degree [1/1]. Doing the numerics (Remez algorithm), one finds

$$ g(x) = \frac{p(x)}{q(x)} = \frac{9.8473383 - 3.9958133 x}{9.8377958 + x} \tag 3 $$

where the function is normalized so that coefficient $q_1=1$. The coefficients of the numerator and denominator polynomial only loosely resemble the values of $\cos \approx(\pi^2-4x^2)/(\pi^2+x^2)$ worked out in the other answer.

The absolte error is given by

$$ \max_{x\in[0,\pi^2/4]} |g(x)-f(x)| = \max_{|x|\leqslant \pi/2} |g(x^2)-\cos(x)| < 0.00097 \tag 4$$ which is an accuracy of around 3 decimals or almost exactly 10 bits.

Plot: Absolute error of $g(x^2)$ against $\cos(x)$ for $|x|\leqslant\pi/2$.

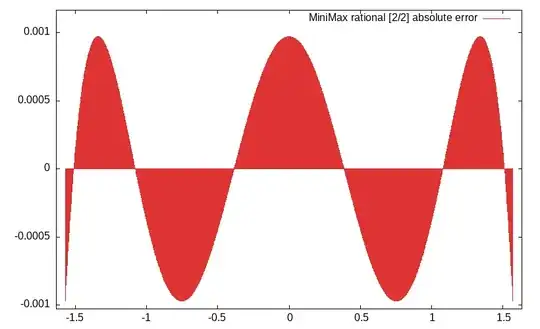
Absolute error of g(x^2) against cos(x)

The optimality of $g(x)$ (or of $g(x^2)$ for that matter) follows from the alternant property of the absolute error: If $\Delta=\max|g-f|$ the absolute error oscillates between $+\Delta$ and $-\Delta$ which is nicely demonstrated by the plot above.

In contrast, the non-optimality of the classic

$$ \frac{\pi^2-4x^2}{\pi^2+x^2} \tag 5$$

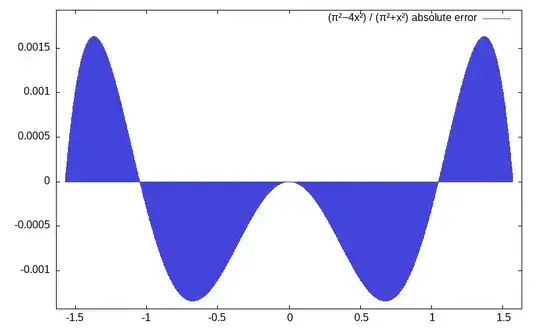
is immediately clear from the plot below because the absolue error does not oscillate nicely with constant "amplitude".

Plot: Absolute error of $(π²−4x²)/(π²+x²)$ against $\cos(x)$ for $|x|\leqslant\pi/2$. Absolute error of classic (pi²-4x²) / (pi²+x²)

Conclusion

  • The classic $(\pi^2-4x^2)/(\pi^2+x^2)$ has an absolute error of ca. $1.63\cdot 10^{-3}$, whereas the optimal $$ g(x^2) = \frac{9.8473383 - 3.9958133 x^2}{9.8377958 + x^2} \tag6 $$ has an absolute error of less than $10^{-3}$.

  • $g(x^2)$ is the best approximation in terms of absolute error amongst all rational functions of degree [2/2] or less.

  • Desmos plot of approximations and their absolute errors

Relative Error

For optimizing the relative error, the situation is similar: The classic formula is sub-optimal, and we can numerically approch the best possible rational function of degree [2/2].

As $\cos$ has zeros at $\pm\pi/2$, we have to divide them out so that the relative error is well-behaved. Using Remez, we find:

$$ \frac{\cos x}{(\frac\pi2-x)(\frac\pi2+x)} \approx r(x)=\frac{3.676844}{9.030178 + x^2} \tag7 $$ with a relative error of $0.0047$ over the target interval as shown by the following plot.

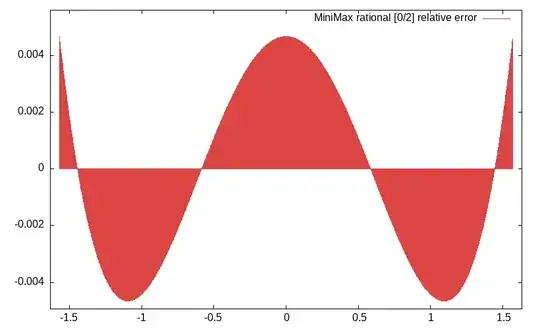
Relative error of r(x)(pi/2-x)(pi/2+x) against cos(x)

Hence, the best approximation in terms of relative error amongst all rational functions of degree [2/2] or less is:

$$ r(x)\left(\frac{\pi^2}4-x^2\right) = \frac{3.676844}{9.030178 + x^2}\left(\frac{\pi^2}4-x^2\right) \tag8 $$

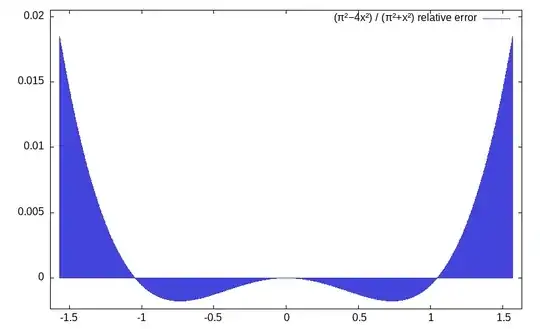
The relative error of the classic approximaton is around $0.019$, which is 4 times the relative error of $(8)$. Absolute error of classic (pi²-4x²) / (pi²+x²)

Desmos plot of approximations and their relative errors

Improving the Results by using Polynomials of Degree 4

The best approximation in terms of absolute error and degree [2/2] is $g(x^2)$ given by $(6)$ with an absolute error around below 0.001.

Evaluating $g$ costs: 1 division, 2 multiplications and 2 additions.

The question is whether this result can be improved with the same or less compute. This is actually the case:

$$ 0.99940323 + x^2 (-0.49558085 + 0.036791683 x^2) \tag 9 $$

costs 3 multiplications and 2 additions. As divisions are usually not cheaper than multiplications, this is an improvement compute-wise, and the absolut error is below 0.0006 which is just 60% of the absolute error of $g$ and just 37% of the absolute error of Bhāskara's $(5)$.

The situation with relative error can also be improved:

$$ (0.4042199 - 0.03515697 x^2)\left(\frac{\pi^2}4 - x^2\right) \tag{10} $$ has a relative error of less than 0.0027 over the target interval, which is only 58% of the error of $(8)$, and only 15% of the relative error of Bhāskara's $(5)$.

Both $(8)$ and $(10)$ have the alternante property, which means that these polynomials are the best ones amongst all polynomials of degree 4 or less.

emacs drives me nuts
  • 10,390
  • 2
  • 12
  • 31
  • Is it interesting for you to discuss solution by polynomials with 4 coefficients and 1e-11 absolute error ? – minorlogic Oct 20 '23 at 11:19