1

I usually don't see any expressions for approximate calculation of trigonometric functions aside from their Taylor series.

But Taylor series work better for small angles, so in general they are not the best way to calculate these functions.

But there is another obvious way to approximate $\cos(x)$:

$$ \cos(x)=2\cos^2\left(\frac{x}{2}\right)-1=2\left(2 \cos^2\left(\frac{x}{4}\right)-1 \right)^2-1=\dots $$

Soon enough we get to small angles, and we can use the first two terms of Taylor series:

$$ \cos\left(\frac{x}{2^n}\right) \approx 1-\frac{x^2}{2^{2n+1}} $$

We obtain the following sequence of approximations to $\cos(x)$:

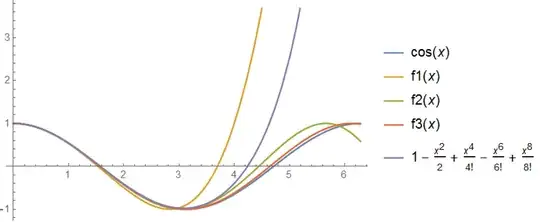
$$ f_1(x)=2\left(1-\frac{x^2}{2^{3}}\right)^2-1 $$

$$ f_2(x)=2\left(2\left(1-\frac{x^2}{2^{5}}\right)^2-1\right)^2-1 $$

$$ f_3(x)=2\left(2\left(2\left(1-\frac{x^2}{2^{7}}\right)^2-1\right)^2-1\right)^2-1 $$

For the angles in the range $0<x<\frac{\pi}{2}$ Taylor expansion of the same order fits better. On the other hand, for larger angles this method is superior, as you can see from the graphs.

cos(x), f1, f2, f3

So, is this method widely known? Can it be useful for calculating trig functions in some cases?

I want to also stress, that while $\cos(x)$ is periodic and we don't need to calculate it for large $x$, the same method can be used to calculate $\cosh(x)$ (the only change will be the sign before $\frac{x^2}{2^{2n+1}}$).

We can use it to calculate the number $e$, with the relation:

$$e=\cosh(1)+\sqrt{\cosh^2(1)-1}$$

 Do[A0 = 1 + 1/2^{2 n + 1};
 Do[A1 = 2*A0^2 - 1;
 A0 = N[A1, 47], {j, 1, n}];
 Print[n, " ", N[A0 + Sqrt[A0^2 - 1], 17]], {n, 1, 14}]

At $14$ recursion steps we obtain the following value for $e$, correct to 9 digits:

$$e=2.718281828...$$

Yuriy S
  • 31,474

1 Answers1

3

The computation of trig functions is usually done by reducing the argument to a relatively small range, such as $0 \le x \le \pi/4$.

Once this is done, there are many ways to compute the function (cordic, pade approximations, table lookup + interpolation, chebychev approximation, ...). Taylor series are not used because they are good at a single point and get worse away from that point.

Finally, if necessary, the result is mapped back to the original argument.

So, your approximations, while interesting, would probably not be used.

marty cohen
  • 107,799
  • On the other hand, my approximation can be used for $\cosh(x)$ as well, and it's not periodic – Yuriy S Feb 11 '16 at 11:32
  • In practical implementations, $cosh(x)$ is typically computed via $e^x$, except for arbitrary precision arithmetic, where for high precision it may be more efficient to compute $e^x$ from $cosh(x)$, since the latter requires only half the number of terms in the Taylor expansion. – njuffa Feb 12 '16 at 00:12
  • For small $x$, there is often a special routine to compute $e^x-1$, since this increases precision. So, for such values, $\cosh(x) = \frac12(e^x+e^{-x})= \frac12((e^x-1)+(e^{-x}-1))+1$. – marty cohen Feb 12 '16 at 03:36