I know that sound a bit stupid, but is there a way to calculate basic trigonometric functions mentally like: $$ \sin(x) $$ $$ \cos(x) $$ $$ \tan(x) $$ $$ \arcsin(x) $$ $$ \arccos(x) $$ $$ \arctan(x) $$ I know it's a lot of functions, but if you can give me a simple and nice writen answer, that would be very nice!
-
1You can for example calculate them with power series expansions or using geometry, looking at the unit circle or triangles. – mathreadler Jan 30 '17 at 05:55
-
1There is no real point in being able to calculate these functions mentally, really. – Mariano Suárez-Álvarez Jan 30 '17 at 06:03
-
@MarianoSuárez-Álvarez I know, but I want just a simple method to approximate those functions – Arthur Guiot Jan 30 '17 at 06:04
-
You google "sin(23 degrees)" and you get an approximation. – Mariano Suárez-Álvarez Jan 30 '17 at 06:09
-
If you remove the "mentally" part then the question becomes one that has interest. – Mariano Suárez-Álvarez Jan 30 '17 at 06:09
-
@MarianoSuárez-Álvarez if you want to answer this question without the mentally, do it, that would be great – Arthur Guiot Jan 30 '17 at 06:11
-
One might consider a digital calculation to be "mental" if mental just means not done using physical writing with pen or book. Empirically the human mind is just electrical signals and a computer is the same. Alternately one could memorize a table of values. – jdods Jun 28 '17 at 11:41
3 Answers
You can use the Taylor Series expansion. For example, $$\sin x= x - \frac{x^3}{3!}+\frac{x^5}{5!}+\dots$$ So as $x \approx 0$ $\sin x \approx x-\frac{x^3}{6}$. Since the error grows a bit larger as $x$ grows, you may also want to use the fact that $\sin x$ is a periodic function. Thus $$\sin(x+2 \pi)=\sin x$$ You can calculate $\cos$ and other trigonometric functions in similar ways. For $\cos$, the expansion is $$\cos x = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots$$ And since $\tan x =\frac{\sin x}{\cos x}$, you can calculate the tangent as well. Other tools you could use include the double angle formula, and you can approximate using well known values such as $$\sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}, \quad \sin \frac{\pi}{6}=\frac{1}{2}, \quad \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$ Or, somewhat less known but still famous $$\sin \frac{\pi}{12}=\frac{\sqrt{6}-\sqrt{2}}{4}$$ For the inverse trigonometric functions, the Taylor series for $\arcsin$ is as follows $$\arcsin x=x+\frac{1!!}{2!!}\frac{x^3}{3}+\frac{3!!}{4!!}\frac{x^5}{5}+\dots$$Where $n!!$ is the double factorial.Then, we have that $\arccos x=\frac{\pi}{2}-\arcsin x$. Using these, we can approximate the values required.
- 22,768
-
Also double angle formulas can let you push closer to 0 giving better approximations. – mathreadler Jan 30 '17 at 05:58
-
-
-
-
-
@S.C.B. Your edit almost complete my question, do the arcsin, arccos, and arctan, and I will click on the check button :) but thanks a lot – Arthur Guiot Jan 30 '17 at 06:06
-
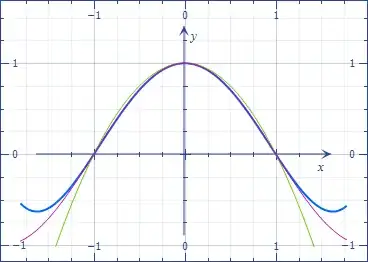
Convert the argument to a multiple of $\pi/2\approx1.57$, i.e. express the angle in "quadrants". It is an easy matter to reduce to the first quadrant.
Then
$$\cos x^*\approx 1-x^2$$ is a resonable approximation ($<5\%$ maximum error, green curve).
You can get better with an extra term,
$$\cos x^*\approx(1-x^2)\left(1-\frac{\pi^2-8}8x^2\right)\approx(1-x^2)\left(1-\frac7{30}x^2\right).$$
($<0.3\%$, blue curve.)
The sine is obtained from $\sin x^*=\cos(1-x^*)$ and the tangent from the ratio. The arc sine/cosine can be drawn form the first approximation, but require a square root extraction, which is uneasy.
-
-
@Lucian: no surprise, these are mere polynomial approximations with some tradeoff between accuracy and coefficient simplicity. – Jan 30 '17 at 08:48
Sorry, but it can't be done mentally. And I don't know about inverse functions but I can give you my simple method to calculate $\sin$ of any angle upto at least one digit of accuracy. First, convert your angle to radians if it's in degrees.
If you want to calculate $\sin\theta$ where $\theta$ is in degrees, then first calculate $x=\frac{\pi\theta}{180}$
Now, if $\theta$ lies between 0 and 22.5 degrees, then $\sin\theta=x$ approximately. The accuracy decreases as the angle increases.
If $\theta$ lies between 22.5 and 45 degrees, then $\sin\theta=x\sqrt{1-(\frac{x}{2})^2}$ approximately. The closer $\theta$ is to 45 degrees, the lesser the accuracy.
If $\theta$ lies between 45 and 67.5 degrees, then use $\sin\theta=\frac{1}{\sqrt{2}}(x-\frac{\pi}{4}+\sqrt{1-(x-\frac{\pi}{4})^2})$. Accuracy decreases as $\theta$ gets closer to 67.5 degrees.
If $\theta$ lies between 67.5 and 90 degrees, use $\sin\theta=\sqrt{1-(\frac{\pi}{2}-x)^2}$. Accuracy increases as $\theta$ gets closer to 90 degrees.
- 588