3

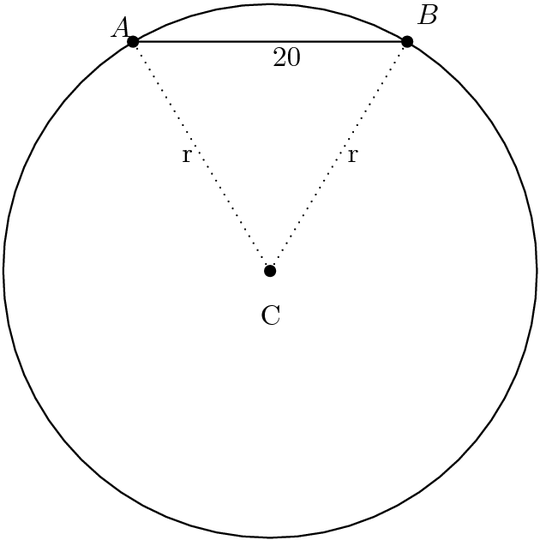
I have been working on a problem for a few days now. This was a challenge problem on a lecture for Trigonometry. I managed to find an equation for the radius, but wasn't able to solve it.

Problem: Line $AB$ is drawn such that $\overline{AB} = 20$. Minor arc $AB$ is drawn with endpoints $AB$ such that the length of arc $AB$ is $21$. Find the area of the region bounded by the arc and the line.

Progress: First, draw the full diagram as shown below.

Full Diagram

We can compute the area of $\angle{ABC}$. Using the Law of Cosines, we have that \begin{align*} \cos C &= \frac{a^2+b^2-c^2}{2ab} \\ &= \frac{2r^2-400}{2r^2}\\ &= 1-\frac{200}{r^2} \end{align*}Therefore, $\angle ACB = \cos^{-1}\left(1-\frac{200}{r^2}\right)$. The length of the arc in terms of $\angle ACB$ is \begin{align*} &\frac{\angle ACB}{360}2\pi r \\ &= \frac{\angle ACB}{180}\pi r \\ &= \frac{\cos^{-1}\left(1-\frac{200}{r^2}\right)}{180}\pi r \end{align*}We know that \begin{align*} &21 = \frac{\cos^{-1}\left(1-\frac{200}{r^2}\right)}{180}\pi r \implies \\&\frac{3780}{\pi r} = {\cos^{-1}\left(1-\frac{200}{r^2}\right)} \implies\\ &\cos\left(\frac{3780}{\pi r}\right) = 1-\frac{200}{r^2} \end{align*} However, I couldn't solve this equation. Any help would be appreciated. I can also visualize a calculus approach involving finding the area between two curves, but I want to solve it in an elementary way if possible.

Nairit
  • 517
  • 2
    If $\theta$ is the angle at $C$ (in radians), then $\theta r= 21$ and $r \sin(\theta/2) = 10$. I used a computer to get $\theta \approx 1.0768$ and $r \approx 19.5018$, and the final area is $r^2\theta/2 - 10\sqrt{r^2-100}\approx 37.34$. As far as I can tell this is not something you can solve without some numerical approximation, but perhaps I am not being clever enough. – angryavian Aug 08 '17 at 20:30
  • Wolfram Alpha gave up on this with standard computation time, so I it is possible that you are right. – Nairit Aug 08 '17 at 20:36
  • I actually did use Wolfram Alpha to solve $\theta / \sin(\theta/2) = 2.1$. – angryavian Aug 08 '17 at 20:57

2 Answers2

1

hint

Let $t $ be the angle $\angle ACB .$

Then

$$21=rt $$

and

$$r\sin(t/2)=10 .$$ the area we want is the difference

$$S=\frac {r^2}{2}t-\frac{20.h}{2} $$ with $$h=r\cos(t/2) $$

hence

$$S=\frac {21}{2}r-10\sqrt {r^2-100} $$

with $r $ satisfying $$r\sin (\frac {21}{2}r)=10$$

hamam_Abdallah
  • 62,951
1

As angryavian commented, the problem reduces to : find the zero of $$f(\theta)=\frac \theta {\sin\left(\frac\theta 2\right)}- 2.1\qquad \text{or}\qquad g(\theta)=\theta-2.1{\sin\left(\frac\theta 2\right)}$$ which can only be solved using numerical methods.

Let $x=\frac\theta 2$ to make the equation $$x=1.05 \sin(x)$$ and use, for an approximation, the magnificent $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ was proposed by Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician (see here).

Skipping the trivial $x=0$, this leads to the quadratic $$4 x^2+\left(\frac{84}{5}-4 \pi \right) x+\pi\left(5 \pi -\frac{84 }{5}\right)=0$$ the positive solution of which being $$x=-\frac{21}{10}+\frac{\pi }{2}+\frac{1}{40} \sqrt{7056+3360 \pi -1600 \pi ^2}\approx 0.537445$$ making $$\theta \approx 1.07489$$ while the exact solution would be $\approx 1.07682$.

With this first result, we could use a Taylor expansion around $\theta=\frac \pi 3$ and get $$g(\theta)=\left(\frac{\pi }{3}-\frac{21}{20}\right)+\left(1-\frac{21 \sqrt{3}}{40}\right) \left(\theta-\frac{\pi }{3}\right)+\frac{21}{160} \left(\theta-\frac{\pi }{3}\right)^2+O\left(\left(\theta-\frac{\pi }{3}\right)^3\right)$$ Ignoring the higher order terms, another quadratic leading to $$\theta \approx 1.07683$$

Claude Leibovici
  • 260,315