30

An Indian mathematician, Bhaskara I, gave the following amazing approximation of the sine (I checked the graph and some values, and the approximation is truly impressive.)

$$\sin x \approx \frac{{16x\left( {\pi - x} \right)}}{{5{\pi ^2} - 4x\left( {\pi - x} \right)}}$$

for $(0,\pi)$

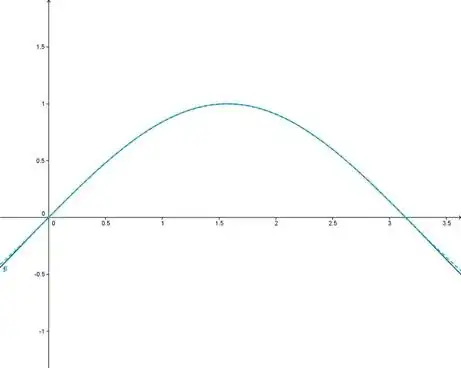
Here's an image. Cyan for the sine and blue for the approximation. enter image description here

¿Is there any way of proving such rational approximation? ¿Is there any theory similar to Taylor's or Power Series for rational approximations?

Pedro
  • 122,002
  • 7
    Off topic: May be you could say Indian Mathematician rather than a Hindu-Mathematician which attaches a religion to Mathematics. (Note: I am Hindu and not against any religion!) –  Feb 06 '12 at 18:59
  • 1
    @KannappanSampath: Edited accordingly :) –  Feb 06 '12 at 19:05
  • 2
    @KannappanSampath That is product of my own ignorance. I translated from my language, which uses "Hindú" for "Indian" ("Hinduista" is "Hindu", whereas "Indio" rather means native indian, and would be used for the people in cowboy movies). – Pedro Feb 06 '12 at 19:06
  • 2
    There is the theory of Padé approximants, but I don't think this particular function is one. –  Feb 06 '12 at 19:06
  • @Peter: I have changed the title. Hope it doesn't affect you. –  Feb 06 '12 at 19:35
  • You can compute the Taylor series of the difference between this function and sine around $\frac{\pi}{2}$. I think the leading term is $\left(\frac{1}{2}-\frac{5}{\pi^2}\right) x^2 \approx -0.0066 x^2$. (At least, that's what I got by converting the approximation into an approximation for cos and then expanding the difference. – Peter Taylor Feb 06 '12 at 19:37
  • @Chandrasekhar Was it too subjective? – Pedro Feb 06 '12 at 19:43
  • 2
    @Peter: Well, i thought including Bhaskara's name in the question would be better because, if some unknown person wants to search something attributed to Bhaskara he may see this question in future :) –  Feb 06 '12 at 19:45
  • 'which attaches a religion to Mathematics' and yet if you attach politics to mathematics its okay - quite bizzar! – onepound Jun 29 '19 at 09:57
  • https://datagenetics.com/blog/july12019/index.html – Juha P May 13 '21 at 20:20

4 Answers4

21

This is very close to a Padé approximant, and in this case the formula is simple enough that it's easy to derive. Firstly, we know that $\sin(x)$ is $0$ at $x=0, x=\pi$; this suggests recasting in terms of the variable $y=x(\pi-x)$. What we're after is a first-order rational approximation $\sin(x) = f(y) = \frac{ay+b}{cy+d}$; since we know that $f(y) = 0$ at $y=0$ (i.e., as $x$ approaches $0$ or $\pi$) then the constant term in the numerator is $0$, and after dividing out the approximation takes the form $\frac{y}{a+by}$.

Now, we certainly want our approximation to give $\sin(\pi/2) = f(\pi^2/4) = 1$; this means $\displaystyle{\frac{\pi^2/4}{a+b\pi^2/4}} = 1$, or $4a+b\pi^2 = \pi^2$, or $a=\frac{1-b}{4}\pi^2$. The other relation between $a$ and $b$ presumably comes from trying to match the derivative at $0$, $\left.d(\sin(x))/dx\right|_{x=0} = 1$; the condition for this this can easily be written out in terms of $df/dy$ at $y=0$. I'll spare the arithmetic (unless someone's really curious), but the result works out to be that $a=\pi$; this would give $b=(\pi-4)/\pi$ and the overall approximant $f(y) = \frac{\pi y}{\pi^2+(\pi-4)y}$, but instead the formula uses a second approximation by setting $a=5\pi^2/16$, which (thanks to the first relation) gives a rational value of $b$ (and in fact, the 'nice' value $1/4$). This approximation is equivalent to saying that $5\pi^2/16\approx\pi$, or in other words that $\pi\approx 16/5 = 3.2$; it means a slight error in the slope of the approximation at $x=0$, but that's a fair tradeoff for the ease of calculation gained.

Steven Stadnicki
  • 51,746
  • Thank you for the answer. Upvoted. I chose the other since he provided me a full article with an explanation. – Pedro Feb 06 '12 at 20:24
  • Wholly understandable! (Note that the article gives a different derivation of the approximation $5\pi^2/16$ for $a$; it satisfies the relation that $\sin(\pi/6) = 1/2$, which keeps $b$ and $a/\pi^2$ rational at all steps). – Steven Stadnicki Feb 06 '12 at 20:49
  • 1
    (Since that's the only other relation of the form $\sin(p\cdot\pi)=q$ for rational $p,q$ this makes quite a bit of sense.) – Steven Stadnicki Feb 06 '12 at 21:04
  • How did you get the article? – Pedro Feb 06 '12 at 21:29
  • @Peter I don't have JSTOR access, but the second link (the one directly to a PDF) in Chandrasekhar's reply worked for me; that PDF is the article I was referring to. – Steven Stadnicki Feb 06 '12 at 22:07
  • 2
    Analogous to taking $\pi \approx 16/5$ to get the correct gradient at $x=0$, you can take $\pi \approx \sqrt{10}$ to get the correct second differential at $x=\pi/2$. – Peter Taylor Feb 06 '12 at 22:34
  • 1
    As it turns out, the derivation given here is similar to what might be done for what is called a "two-point Padé approximant". – J. M. ain't a mathematician Mar 24 '12 at 10:43
  • 1
    @PedroTamaroff isn't it against site policy to submit answers that are just links? Made worse in this case by paywall and dead links. (The possibility of which is of course the reason for the policy). I think you should accept Steven's answer instead. – ziggurism Aug 07 '18 at 17:33
11

Writing $x = \pi/2 + \pi t$, the approximation becomes $\cos(\pi t) \approx \frac{1-4t^2}{1+t^2} = 1 - 5 t^2 + O(t^4)$. In fact $\cos(\pi t) = 1 - \frac{\pi^2}{2} t^2 + O(t^4)$, but $\pi^2/2 \approx 4.9348$ is not far from $5$. In terms of uniform approximation to $\cos(\pi t)$ for $t \in [-1/2, 1/2]$, $\frac{1 - 4 t^2}{1+1.0043 t^2}$ would be somewhat better.

Robert Israel
  • 448,999
  • Actually, putting $\cos \frac{\pi x}{2} $ gives what in the article is stated as the "Bhaskara function":$$\cos \frac{\pi x}{2} \approx 4 \frac{1-x^2}{4+x^2}$$ which is an outstoundingly good approximation of that function. Thanks! – Pedro Feb 10 '12 at 03:17
6

  • Here is an article which is written by Shailesh Shirali. Unfotunately my university doesn't have access to it.

  • Here is one more article.

1

That's a pretty neat visualization of how can you intiutively build, proove and understand the approximation. enter image description here

The full proof with video and explanation.

Tatar Elemér
  • 276