2

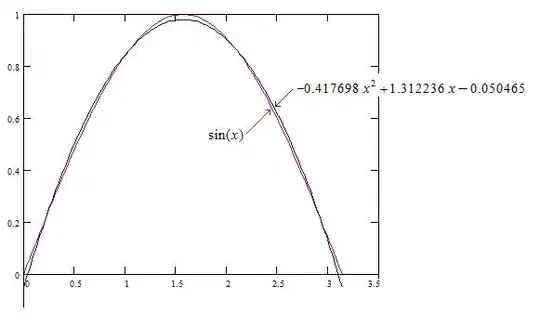
Problem Find a parabola ($f(x)=ax^2+bx+c$) that approximate the function sine the best on interval [0,$\pi$].

The distance between two solutions is calculated this way (in relation to scalar product): $\langle u,v \rangle=\int_0^\pi fg$.

My (wrong) solution I thought that I would get the solution by calculating the orthogonal projection $w=a+bx+cx^2$ of $v=\sin x$ on subspace $W=\langle u_1,u_2,u_3 \rangle=\langle 1,x,x^2\rangle$ using Gramm matrix. Then I have $$\begin{pmatrix}\langle u_1, u_1\rangle&\langle u_1, u_2\rangle&\langle u_1, u_3\rangle\\ \langle u_2, u_1\rangle&\langle u_2, u_2\rangle&\langle u_2, u_3\rangle\\ \langle u_3, u_1\rangle&\langle u_3, u_2\rangle& \langle u_3, u_3\rangle\end{pmatrix} \begin{pmatrix} a\\b\\c\end{pmatrix}= \begin{pmatrix} \langle u_1, v\rangle\\ \langle u_2,v\rangle\\ \langle u_3, v\rangle \end{pmatrix}$$ So then $$\begin{pmatrix} \int_0^\pi 1&\int_0^\pi x&\int_0^\pi x^2\\ \int_0^\pi x& \int_0^\pi x^2& \int_0^\pi x^3 \\ \int_0^\pi x^2&\int_0^\pi x^3&\int_0^\pi x^4\end{pmatrix}\begin{pmatrix} a\\b\\c\end{pmatrix}=\begin{pmatrix} \int_0^\pi \sin x\\\int_0^\pi x\sin x\\\int_0^\pi x^2 \sin x \end{pmatrix}$$ But solving these equations didn't give me any good answer. So my question is - is my way of solving it completely wrong (if so, can you give me hints how to do it otherwise)?

Thank you

Edit Then$$ \begin{pmatrix} \pi&\frac{\pi^2}{2}&\frac{\pi^3}{3}\\ \frac{\pi^2}{2}&\frac{\pi^3}{3}&\frac{\pi^4}{4}\\ \frac{\pi^3}{3}&\frac{\pi^4}{4}&\frac{\pi^5}{5}\end{pmatrix}\begin{pmatrix} a\\b\\c\end{pmatrix}=\begin{pmatrix} 2\\\pi\\\pi^2-4 \end{pmatrix}$$ $$ \begin{pmatrix} \pi&\frac{\pi^2}{2}&\frac{\pi^3}{3}\\ 0&\frac{\pi^3}{12}&\frac{\pi^4}{12}\\ 0&\frac{\pi^4}{12}&\frac{4\pi^5}{45}\end{pmatrix}\begin{pmatrix} a\\b\\c\end{pmatrix}=\begin{pmatrix} 2\\0\\\frac{1}{3}\pi^2-4 \end{pmatrix}$$ $$ \begin{pmatrix} \pi&\frac{\pi^2}{2}&\frac{\pi^3}{3}\\ 0&\frac{\pi^3}{12}&\frac{\pi^4}{12}\\ 0&0&\frac{\pi^5}{180}\end{pmatrix}\begin{pmatrix} a\\b\\c\end{pmatrix}=\begin{pmatrix} 2\\0\\\frac{1}{3}\pi^2-4 \end{pmatrix}$$ Edit II My way (I have found the mistake I did) will get the result $$f(x)=\dfrac{60(\pi^2-12)}{\pi^5}x^2-\dfrac{60(\pi^2-12)}{\pi^4}x+\dfrac{12(\pi^2-10)}{\pi^3}$$ which I hope is the right answer with error approx. $0,000936$

GorTeX
  • 553
  • 1
    That looks right to me. You might try the basis $1,x-\pi/2,(x-\pi/2)^2$ because the second coefficient will turn out to be zero as $\sin x$ is even about $\pi/2$. – Empy2 Mar 21 '15 at 16:32
  • When I get the solution, I put it into Wolfram and I got a parabola that didn't look much as sine. Then I tried to calculate it once more, but get even worse solution :-) So I will try it once more with different basis... – GorTeX Mar 21 '15 at 16:36
  • Is there a reason you don't want to use Taylor series? – Demosthene Mar 21 '15 at 16:37
  • I even did it using Taylor series, but then I remembered that we did something similar (Gramm matrices) on linear algebra. So I wanted to try it, but the results weren't the same – GorTeX Mar 21 '15 at 16:41
  • 1
    On a side note, why is the distance between the two functions given by $\int fg$? Say $f=g$, the distance should be $0$, which is clearly not equal to $\int f^2$. – Demosthene Mar 21 '15 at 16:50
  • $\cos\bigg(\dfrac\pi2~x\bigg)~\simeq~\big(1-x^2\big) ~\bigg(1-\dfrac{x^2}{4.5}\bigg),~$ for $|x|<1.~$ See Bhaskara I's sine approximation formula, as well as this post. – Lucian Mar 21 '15 at 17:03

4 Answers4

1

Hint

By similarity with least square fit problems, I think that you need to minimize $$F=\int_0^{\pi}\Big(\sin(x)-(a x^2+bx+c)\Big)^2~dx$$ Compute the expression and say that $$\frac{dF}{da}=\frac{dF}{db}=\frac{dF}{dc}=0$$ This will provide three linear equations for the three unknowns $a,b,c$.

This seems to be very similar to what you posted (and the result is quite good).

Edited later

The answer you obtained is perfectly right but, if I may, I would like to add a comment about the problem itself. Fist, you notices that the function does not reproduce the values of $\sin(x)$ at the bounds.

As mentioned by Lucian, almost 1400 years ago, Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician and astronomer, proposed for the sine developements in terms of $x(\pi-x)$. So, let me consider the approximation $$\sin(x)\approx \sum_{i=1}^j a_i \big(x(\pi-x)\big)^i$$ (I excluded constant terms in order the values of $\sin(x)$ at the bounds be respected) and repeat the calculations as you made them (you could notice from your final result that the expression corresponds to $j=1$ plus a constant term).

For $j=1$, $F=2.27 \times 10^{-3}$ which is effectively worse than the $9.36 \times 10^{-4}$ you obtained (because I omitted the constant term).

For $j=2$, $F=7.89 \times 10^{-7}$ which is much better.

For $j=3$, $F=6.77 \times 10^{-10}$ which is much much better.

This was just to show that, depending on the base function we select, for the same number of adjustable parameters (or even less), we can make approximations of very different quality.

Just for your curiosity, the marvelous approximation given 1400 years ago $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}$$ leads to $F=2.98 \times 10^{-6}$.

Claude Leibovici
  • 260,315
  • So I must have done a mistake during the calculations. Can I ask you, how does it give the same solution(matrix) as mine? Thx – GorTeX Mar 21 '15 at 16:49
  • May I confess that I am very bad with matrix problem but it looks that your formulation and mine are identical (if you put mine on a matrix form). May be, you have a mistake in some of the integrals. For the rhs, the values are $2,\pi,\pi^2-4$. – Claude Leibovici Mar 21 '15 at 16:51
  • Thx, I am not that good with integrals, but I used wolfram for that, so I hope that they are right (the rhs is the same) – GorTeX Mar 21 '15 at 17:03
  • In the lhs, they are very simple. – Claude Leibovici Mar 21 '15 at 17:05
  • Just for sure - I should get the same result as by using Taylor series of order 2 for sin x, shouldn't I? – GorTeX Mar 21 '15 at 17:05
  • Not at all. Taylor series built at $x=0$ would give $a=0,b=1,c=0$ – Claude Leibovici Mar 21 '15 at 17:11
  • I have added more steps - do you happen to see any mistake there? thx – GorTeX Mar 21 '15 at 17:23
  • Sry, but I don't know how to write the extended matrix in LaTex so I have to do it this way :-) – GorTeX Mar 21 '15 at 17:24
  • I put the last (my) equations to wolfram and it seems to be right - I must have been doing some stupid mistakes, but at the beginning I wasnt sure whether my solution was right - nevertheless, thanks for help – GorTeX Mar 21 '15 at 17:48
-1

First,I donnot think the orthogonal projection is proper here. The orthogonal projections are often used to make infinity series to approach function,because the coefficients there is more simple,you can try to use error square or the maximun of error

user225373
  • 1
-1

The answer has already been given.

In addition, the numerical solving and the graph are shown below, in order to compare the results.

enter image description here enter image description here

Note that the result corresponds to the mean least square absolute deviation. A small modification of the method and formulas would give the result corresponding to the mean least square relative deviation, which could be more convenient in the low range of $\sin(x)$.

JJacquelin
  • 66,221
  • 3
  • 37
  • 87
-2

Is not the direct modern equivalent of Bhaskara's parabola approximation for Sine curve good enough as a start?

$$ y(x) = \dfrac{x(\pi-x)}{2},$$ $$ y(\pi/2)= \pi^2/8;y^{'}(\pi/2) =0; y^{''}(\pi/2) =-1. $$

And cannot the amplitude alone be improved/adjusted from here further to minimize error by least squares?

Narasimham
  • 40,495