17

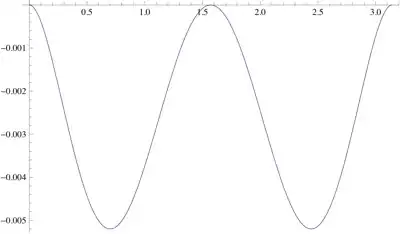
Being fascinated by the approximation $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ proposed, more than 1400 years ago by Mahabhaskariya of Bhaskara I (a seventh-century Indian mathematician) (see here), I considered the function $$\sin \left(\frac{1}{2} \left(\pi -\sqrt{\pi ^2-4 y}\right)\right)$$ which I expanded as a Taylor series around $y=0$. This gives $$\sin \left(\frac{1}{2} \left(\pi -\sqrt{\pi ^2-4 y}\right)\right)=\frac{y}{\pi }+\frac{y^2}{\pi ^3}+\left(\frac{2}{\pi ^5}-\frac{1}{6 \pi ^3}\right) y^3+O\left(y^4\right)$$ Now, I made (and may be, this is not allowed) $y=(\pi-x)x$. Replacing, I obtain $$\sin(x)=\frac{(\pi -x) x}{\pi }+\frac{(\pi -x)^2 x^2}{\pi ^3}+\left(\frac{2}{\pi ^5}-\frac{1}{6 \pi ^3}\right) (\pi -x)^3 x^3+\cdots$$ I did not add the $O\left(.\right)$ on purpose since not feeeling very comfortable.

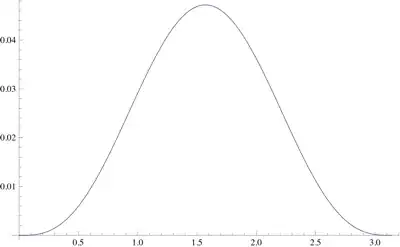
What is really beautiful is that the last expansion matches almost exactly the function $\sin(x)$ for the considered range $(0\leq x\leq\pi)$ and it can be very useful for easy and simple approximate evaluations of definite integrals such as$$I_a(x)=\int_0^x \frac{\sin(t)}{t^a}\,dt$$ under the conditions $(0\leq x\leq \pi)$ and $a<2$.

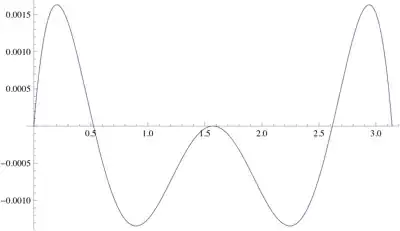
I could do the same with the simplest Padé approximant and obtain $$\sin(x)\approx \frac{(\pi -x) x}{\pi \left(1-\frac{(\pi -x) x}{\pi ^2}\right)}=\frac{5\pi(\pi -x) x}{5\pi ^2-5(\pi -x) x}$$ which, for sure, is far to be as good as the magnificent approximation given at the beginning of the post but which is not very very bad (except around $x=\frac \pi 2$).

The problem is that I am not sure that I have the right of doing things like that.

I would greatly appreciate if you could tell me what I am doing wrong and/or illegal using such an approach.

Edit

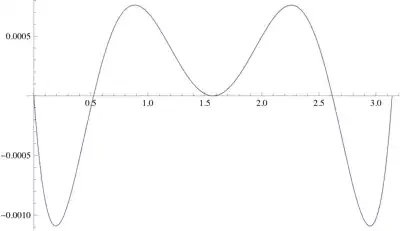
After robjohn's answer and recommendations, I improved the approximation writing as an approximant $$f_n(x)=\sum_{i=1}^n a_i \big(\pi-x)x\big)^i$$ and minimized $$S_n=\int_0^\pi\big(\sin(x)-f_n(x)\big)^2$$ with respect to the $a_i$'s.

What is obtained is $$a_1=\frac{60480 \left(4290-484 \pi ^2+5 \pi ^4\right)}{\pi ^9} \approx 0.31838690$$ $$a_2=-\frac{166320 \left(18720-2104 \pi ^2+21 \pi ^4\right)}{\pi ^{11}}\approx 0.03208100$$ $$a_3=\frac{720720 \left(11880-1332 \pi ^2+13 \pi ^4\right)}{\pi ^{13}}\approx 0.00127113$$ These values are not very far from those given by Taylor ($\approx 0.31830989$), ($\approx 0.03225153$), ($\approx 0.00116027$) but, as shown below, they change very drastically the results.

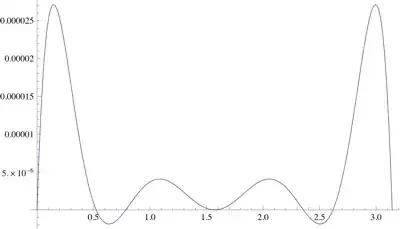
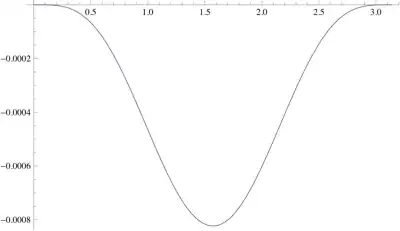
The errors oscillate above and below the zero line and, for the considered range, are all smaller than $10^{-5}$.

After minimization, $S_3\approx 8.67\times 10^{-11}$ while, for the above Taylor series, it was $\approx 6.36\times 10^{-7}$.

Community
  • 1
Claude Leibovici
  • 260,315
  • 1
    The one concern I might have here is that $y=(\pi-x)x$ is not bijective over the range $0 \leq x \leq \pi$. On the other hand, $\sin(x)$ actually only depends on $y$ on this range, because of symmetry. So it seems legitimate to me. – Ian Mar 27 '16 at 14:03
  • 1
    @Ian. I have the same concern from the very beginning. But, if legimate, it is quite amazing, don't you think ? If you want fun, have a look to $I_1(x)$ over the whole range. – Claude Leibovici Mar 27 '16 at 14:06

2 Answers2

6

A few approximations

When making approximations, there is no legal or illegal. There are things that work better and things that don't. When making approximations that are supposed to work over a large range of values, often the plain Taylor series is not the best way to go. Instead, a polynomial or rational function that matches the function at a number of points is better. $$ \frac{\pi(\pi-x)x}{\pi^2-\left(4-\pi\right)(\pi-x)x}\tag{1} $$ matches the values and slopes of $\sin(x)$ at $0$, $\frac\pi2$, and $\pi$. However, it is always low.

enter image description here

If instead, we match the values at $0$, $\frac\pi6$,$\frac\pi2$, $\frac{5\pi}6$, and $\pi$ we get Mahabhaskariya's approximation $$ \frac{16(\pi-x)x}{5\pi^2-4(\pi-x)x}\tag{2} $$ which is both high and low, and the maximal error is about $\frac13$ of the one-sided error.

enter image description here

A good quadratic polynomial approximation also matches the values at $0$, $\frac\pi6$,$\frac\pi2$, $\frac{5\pi}6$, and $\pi$ $$ \frac{31}{10\pi^2}(\pi-x)x+\frac{18}{5\pi^4}(\pi-x)^2x^2\tag{3} $$ enter image description here

The maximal error is about $\frac23$ that of Mahabhaskariya's.

If we want to extend to a cubic polynomial, we can try to match values at $0$, $\frac\pi6$, $\frac\pi4$, $\frac\pi2$ $$ \tfrac{9711-6400\sqrt2}{210\pi^2}(\pi-x)x+\tfrac{-7194+5120\sqrt2}{15\pi^4}(\pi-x)^2x^2+\tfrac{43488-30720\sqrt2}{35\pi^6}(\pi-x)^3x^3\tag{4} $$ enter image description here

The maximum error of approximation $(4)$ is about $\frac1{40}$ that of approximation $(3)$.

Analysis of the functions in the question

The function $$ \frac{\pi(\pi-x)x}{\pi^2-(\pi-x)x}\tag{5} $$ has a maximum error about $40\times$ as big as $(3)$

enter image description here

The function $$ \frac{(\pi-x)x}\pi+\frac{(\pi-x)^2x^2}{\pi^3}+\left(\frac2{\pi^5}-\frac1{6\pi^3}\right)(\pi-x)^3x^3\tag{6} $$ has $30\times$ the maximum error of $(4)$. However, the coefficients of $(6)$ are more appealing.

enter image description here

robjohn
  • 345,667
  • I agree. My problem is that I started solving for $x$ $(\pi-x)x=y$ and tehn made the Taylor expansion of $\sin \left(\frac{1}{2} \left(\pi -\sqrt{\pi ^2-4 y}\right)\right)$ and then changed again in the resulting expression $y$ by $(\pi-x)x$. Is this kind of gymnastics allowed from a purely mathematical point of view ? – Claude Leibovici Mar 27 '16 at 14:50
  • 1
    As I said, there is no right or wrong when making approximations. You are not claiming that things are supposed to converge, just that this is close; how close tells how good the approximation is. – robjohn Mar 27 '16 at 15:49
  • I am unable to make good plots since I do not see them (I am almost blind). My wife told me that the ones you added are very clear and explicit. Would you mind to add, for illustration purposes, the one corresponding to $$\sin(x)=\frac{(\pi -x) x}{\pi }+\frac{(\pi -x)^2 x^2}{\pi ^3}+\left(\frac{2}{\pi ^5}-\frac{1}{6 \pi ^3}\right) (\pi -x)^3 x^3$$. Thank you ! – Claude Leibovici Mar 27 '16 at 16:23
  • Thank you very much. I added some information about what was my next step. – Claude Leibovici Mar 28 '16 at 08:15
  • Thanks for the idea ! What is nice is that, using your last formula, $S$ comes to be $\approx 3.35\times 10^{-10}$ that is to say half of what I obtained after optimization. – Claude Leibovici Mar 29 '16 at 08:46
  • I have been told that I probably faced some working precision issues. In fact, for three terms $S\approx 8.67 \times 10^{-11}$ which is almost four times lower than what it is with your nice expression. One thing I find funny is that, using four terms insted of three, makes $S\approx 3.83 \times 10^{-15}$. In any manner, I am able to compute $I_a(x)$ quite accurately at very low cost (even up to $a=1.9$. – Claude Leibovici Apr 04 '16 at 06:03
  • Is $S$ the mean square ($L^2$) error? Because of the "spikes", that will definitely be lower than the maximum ($L^\infty$) error, which is what my error measurements are. – robjohn Apr 04 '16 at 08:20
  • Five years later Having reworked the problem, minimizing $$\int_0^\pi \Big[\sin(x)-a (\pi-x)x-b(\pi-x)^2x^2\Big]^2,dx$$ I obtain the awful $$a=\frac{1680 \left(11 \pi ^2-108\right)}{\pi ^7}\qquad \text{and} \qquad b=\frac{5040 \left(168-17 \pi ^2\right)}{\pi ^9}$$ which are almost identical to your nice coefficients. – Claude Leibovici May 04 '21 at 09:54
  • @ClaudeLeibovici: it's nice to know that minimizing the mean square of the difference gives almost the same coefficients that matching a polynomial at $5$ points. Thanks. – robjohn May 04 '21 at 22:23
1

@Claude Leibivici use the following two point Taylor series in x=-Pi, Pi $$\frac{z (z-\pi )^3 (z+\pi )^3}{48 \pi ^4}-\frac{5 z (z-\pi )^3 (z+\pi )^3}{16 \pi ^6}+\frac{3 z (z-\pi )^2 (z+\pi )^2}{8 \pi ^4}-\frac{z (z-\pi ) (z+\pi )}{2 \pi ^2}$$ the cuadratic error is superior to any formula above at the same grade

Clerk
  • 129
  • Very interesting ! I suppose typo's : I presume that the first term is $\frac{z (z-\pi )^4 (z+\pi )^4}{48 \pi ^8}$. Is this correct ? – Claude Leibovici Apr 13 '18 at 10:33
  • No is raise Power 4 – Clerk Apr 13 '18 at 10:40
  • Just out of curiosity : do you know any CAS doing two point Taylor series ? – Claude Leibovici Apr 13 '18 at 11:14
  • what it is mean CAS – Clerk Apr 13 '18 at 11:16
  • Computer Algebra System (such as Mahematica, Wolfram Alpha, ...) – Claude Leibovici Apr 13 '18 at 11:18
  • Ah ok i do not Know , there are a paper with a formula but only works for few series and one variable is the only i know – Clerk Apr 13 '18 at 11:24
  • Is there a link to the paper you refer to ? I have some papers with no example at all; just formulae. – Claude Leibovici Apr 13 '18 at 11:28
  • https://arxiv.org/abs/math/0205064 – Clerk Apr 13 '18 at 13:41
  • Claude leibovici I was representing your series and I've noticed that it coincides with the series of taylor around two points, from where you came up with the representation of sin around of $\frac{1}{2} \left(\pi -\sqrt{\pi ^2-4 y}\right)$ the series of sin(xI around two points is $$\left(\frac{5}{\pi ^7}-\frac{1}{2 \pi ^5}\right) z^4 (z-\pi )^4+\left(\frac{1}{6 \pi ^3}-\frac{2}{\pi ^5}\right) z^3 (z-\pi )^3+\frac{z^2 (z-\pi )^2}{\pi ^3}-\frac{z (z-\pi )}{\pi }$$ – Clerk Apr 21 '18 at 18:10