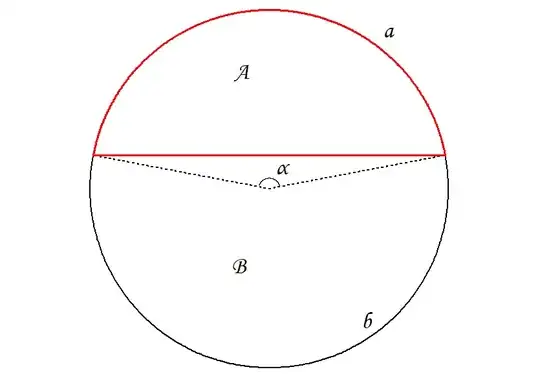
The accepted definition for the golden angle is based on the ratio of circle arcs, i.e. if $\alpha_0$ is the golden angle in radians, then:
$$\frac{a}{b}=\frac{b}{a+b}$$
Where $a=\alpha_0 R$ and $b=(2 \pi-\alpha_0) R$.
If the angle is defined as such then we can show that $\alpha_0=(3- \sqrt{5}) \pi$.
(All of the above is according to Wikipedia).
However, if we use the direct generalization of the common definition for the golden ratio for a line segment, we should be comparing areas instead of arc length. Thus, if $\alpha$ is the (new kind of) golden angle, we should define it using the segment area $A$ that we "cut off" by drawing the chord:
$$A=\frac{1}{2} (\alpha-\sin \alpha)$$
$$\frac{A}{B}=\frac{B}{A+B}$$
We obtain a transcendental equation for the angle:
$$\alpha-\sin \alpha=(3- \sqrt{5}) \pi=2(2-\phi) \pi$$
Numerically its value is:
$$\alpha=2.7664077793984\dots=0.8805749453982892\dots \pi$$
I have not been able to find a closed form.
Can we find a closed form for $\alpha$? Is it an algebraic multiple of $\pi$ or not?
Unlike the common definition, this latter definition of the golden angle can be generalized for the sphere in 3D (cutting by a plane and then comparing volumes) or even the $n-$sphere in any number of dimensions.
If I'm correct, then for a sphere we obtain an equation:
$$(2+\cos (\alpha/2))(1-\cos (\alpha/2))^2=2(3-\sqrt{5})$$
Which makes $\cos \alpha_{3D}$ algebraic and as far as I understand $\alpha_{3D}$ an algebraic multiple of $\pi$.
$$\alpha_{3D}=2.8228221947949\dots=0.898532211542238\dots \pi$$