$\sin 12°=\ldots$ without a scientific calculator

Question

I would like to find the

$$\color{red}{\huge\sin 12°}$$ without a scientific calculator and Maclaurin formula because my students of an high school don't know this approach. I have thought starting from $\sin 18°=(\sqrt 5-1)/4$ and the cosine $\cos 18°=(\sqrt{10}+2\sqrt 5)/4$ (from the geometry we know that the side of the regular decagon is the golden section of the radius).

Being $\sin (2\alpha)=2\sin(\alpha)\cos(\alpha)$ I know $\sin 36°$, but for the $\sin 12°$ I have thought $$\cos3α=\cos(2α+α)=\cos2α\cosα−\sin2α\sinα=$$$$\cosα⋅(2\cos2α−1)−2\sin2α\cosα$$

$$=2\cos3α−\cosα−2\cosα(1−\cos2α)=$$$$2\cos3α−\cosα−2\cosα+2\cos3α=4\cos3α−3\cosα$$ Considering the formulas of trisection of an angle I have: $$\boxed{\cosα=\frac 43\cos3α −3\cos \frac\alpha3}$$ We could put $\cos(α/3)=z$ and thus I will have the equation

$$4z^3-3z-\cosα=0$$

It is then a matter of solving that third degree equation, of which there is a solution method (which reminds me of the famous querelle between Tartaglia and Cardano...).

My problem it is this:

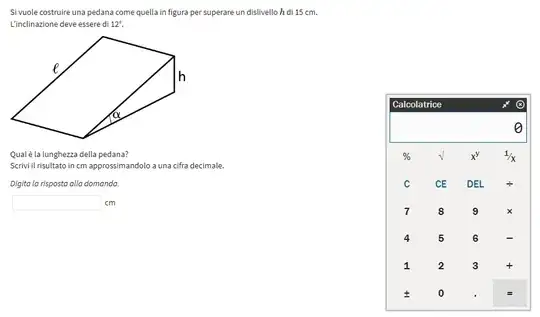
You want to build a platform like the one in the figure to overcome a height difference $h$ of 15 cm. The inclination must be 12°. What is the length $\ell$ of the platform? (the link is https://invalsi.zanichelli.it/taoDelivery/DeliveryServer/runDeliveryExecution?deliveryExecution=kve_de_https%3A%2F%2Finvalsi.zanichelli.it%2Ffirst.rdf%23i164517281905829660045946)

My students have not a scientific calculator during the test.

How can I solve the problem simply?

Answer 1

A $\large 1400^+$ years old approximation is $$\sin (12 {}^{\circ})\sim\frac{224}{1069}$$ which is a relative error of $0.78$% and absolute error of $1.6\times 10^{-3}$.

This will make your students aware that there were very good mathematicians long time ago.

Answer 2

The degree 3 equation has an explicit solution but it is a bit complicated. $$\sin(12^\circ) = {1\over 4} \sqrt{{5+\sqrt{5} \over 2}} -{\sqrt{3}(\sqrt{5}-1)\over 8}$$

As far as I understand, you want an approximation to the value $\sin(12^\circ)$ that may replace the one given by a calculator.

Before the advent of calculators, engineers used the following approximation for the sine, assuming $x$ small, given in degrees. $$ \sin(x) \simeq {x\over 60}$$ In your case, this gives $$\sin(12^\circ) \simeq {12 \over 60} = 0.2$$ This is close to the true value which is $\sin(12^\circ) = 0.20791169081775931$...

Answer 3

It's easy. First, we find the value of $\sin(18^{\circ})$.

Observe that $\sin(36^{\circ})=\cos(54^{\circ})\Longleftrightarrow 2\sin(18^{\circ})\cos(18^{\circ})=\cos(18^{\circ})\cos(36^{\circ})-\sin(18^{\circ})\sin(36^{\circ})$

$\Longleftrightarrow 2\sin(18^{\circ})\cos(18^{\circ})=\cos(18^{\circ})(1-2\sin^2(18^{\circ}))-\sin(18^{\circ})2\sin(18^{\circ})\cos(18^{\circ})$

$\Longleftrightarrow 2\sin(18^{\circ})=1-2\sin^2(18^{\circ})-2\sin^2(18^{\circ})$

$\Longleftrightarrow 4\sin^2(18^{\circ})+2\sin(18^{\circ})-1=0$

Easy to solve quadratic equations. it is obtained that $\sin(18^{\circ})=\dfrac{\sqrt{5}-1}{4}$. By Identity $(\sin^2(x)+\cos^2(x)=1)$. and remembering that $0<\cos(18^{\circ})<1$. we get $\cos(18^{\circ})=\sqrt{\dfrac{5+\sqrt{5}}{8}}$

Now, note that $\cos(18^{\circ})=\sin(72^{\circ})$, $\sin(18^{\circ})=\cos(72^{\circ})$ and $\sin(12^{\circ})=\sin(72^{\circ}-60^{\circ})$.

$\sin(12^{\circ})=\sin(72^{\circ})\cos(60^{\circ})-\cos(72^{\circ})\sin(60^{\circ})$

$$\sin(12^\circ) = {1\over 4} \sqrt{{5+\sqrt{5} \over 2}} -{\sqrt{3}(\sqrt{5}-1)\over 8}$$

With similar step even we can easily find value of $\sin(3^{\circ})=\sin(75^{\circ}-72^{\circ})=\sin(18^{\circ}-15^{\circ})$

and, we can get the approximation value of $\sin(12^{\circ})$ using Newton Method

Answer 4

When an angle is narrow, the hypoteneuse is almost parallel with the adjacent edge and both are close to a pair of radius lines from the centre of a regular $n$-gon to two neighbouring vertices. This gives you $$\sin\theta=\dfrac{\text{opp}}{\text{adj}}\approxeq \dfrac{2\pi\cdot r/n}r=\dfrac{2\pi}n$$

$n$ here is how many edges your $n$-gon has, which in this case is $360/12=30$

Giving you $\approxeq\dfrac{\pi}{15}\approxeq0.209$ which is close to the true value of $0.2079\ldots$

---

If you wanted you could take $\pi$ to be roughly $22/7$ in which case you get the fraction $\dfrac{22}{105}$ which again is good to nearly three decimal places.