4

In the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$, the cosine function superficially resembles an inverted parabola of the form $-ax^2+1$:

enter image description here

I wanted to know more and computed the $L^2$ norm (surrounding square root omitted for readability):

$$ \int_{-\pi/2}^{\pi/2} \,(\cos(x)-(ax^2+1))^2\,dx \quad=\quad \frac{\pi^5 a^2}{80}+\frac{1}{6}(48-6\pi^2+\pi^3) a+\frac{3\pi}{2}-4 $$

Minimizing the expression on the right hand side with respect to $a$ yields the enigmatic solution

$$a=\frac{-20\pi^3+120\pi^2-960}{3\pi^5}=-0.431...$$

which indeed shows a nice agreement:

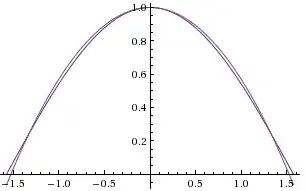
enter image description here

Thus, the parabola $ax^2+1$ with this value for $a$ is in some sense the best parabolic approximation to the cosine in the largest interval in which the cosine is concave like the parabola is.


By now you have probably guessed my question: What is going on? I don't know what I expected the optimum value of $a$ to look like, but this is definitely not it. Where do these "magic" numbers $20$, $120$, $960$ and $3$ come from? Is there any way to understand this result other than computing the integral?

  • 1
    I can't give a "good" answer, but here's a comment. In my experience the coefficients of polynomials of best approximation are almost never nice numbers. Generally I expect them to be a mess, and if a closed form exists then it's a bonus. – Antonio Vargas Nov 16 '14 at 17:06
  • 1
    A related question. – Lucian Nov 16 '14 at 19:53
  • @Lucian: Thank you so much, I had seen that question before and wanted to link to it, I just couldn't find it anymore. –  Nov 17 '14 at 07:14

1 Answers1

2

These rather unexpected and large coefficients arise, in the calculation of the integral and of the successive minimization, only if we search an expression for $a$ where the numerator has no fractional terms and no "collected" factors: in fact, in this case we necessarily have to perform some multiplications that lead to relatively large coefficients. However, if we allow to have fractional terms and collected factors in the numerator, the coefficients become relatively simple.

To understand where these large coefficients come from, it is convenient to analyze the solution step by step and to keep the numbers as "simple" as possible. The initial definite integral is obtained by noting that, considering each term separately, we have

$$\displaystyle \int_{-\pi/2}^{\pi/2} \,\cos^2(x)=\frac{\pi}{2}$$

$$\displaystyle \int_{-\pi/2}^{\pi/2} \,(-2 \cos(x)(ax^2+1))\,dx=(8-\pi^2)a-4$$

$$\displaystyle \int_{-\pi/2}^{\pi/2} \,(ax^2+1)^2\,dx= \frac{\pi^5}{2^4 \cdot 5}a^2+\frac{\pi^3}{6}a +\pi$$

Summing these three espressions, we get that the whole integral is equal to

$$\displaystyle \frac{\pi^5}{2^4 \cdot 5}a^2+(\frac{\pi^3}{6}-\pi^2+8)a+\frac{3\pi}{2}-4 $$

The derivative is

$$\displaystyle \frac{\pi^5}{2^3 \cdot 5}a+( \frac{\pi^3}{6}-\pi^2+8) $$

which equalized to zero and solved for $a$ yields the solution

$$\displaystyle a=\frac{2^3 \cdot 5 ( - \frac{\pi^3}{6}+\pi^2-8)}{ \pi^5}$$

where the coefficients are rather simple and not particularly striking.

However, if we want to eliminate the fractional term in the numerator, we have to collect the quantity $\displaystyle \frac{1}{6}$. This leads to

$$\displaystyle a=\frac{2^3 \cdot 5 ( -\pi^3+6\pi^2-6\cdot 8)}{ 6\pi^5}= \frac{2^2 \cdot 5 ( - \pi^3+6\pi^2-6\cdot 8)}{ 3\pi^5}$$

and multiplying the constant factor $2^2 \cdot 5=20$ for each term in the numerator we get

$$\displaystyle a= \frac{-20 \pi^3+ 20 \cdot 6\pi^2- 20 \cdot 6\cdot 8}{ 3\pi^5} \\= \frac{ -20 \pi^3+120 \pi^2-960}{ 3\pi^5} $$

which is the form reported in the OP.

Anatoly
  • 17,079