Pythagorean theorem expressed without roots in an old Tamilian (Indian) statement

Question

There's an old Tamil statement that predicts the hypotenuse of a right angle triangle to a reasonable level of accuracy considering it doesn't involve roots. This is how it goes:

“Odum Neelam Thanai Ore Ettu Kooru thaaki Koorilae Ondrai Thalli Kundrathil Paadhiyai Saerthal Varuvathu Karnam Thane”

This translates to something like -

"Subtract one eight of the length (longer side) from the length, and add a half of the height to get the hypotenuse". This approximates quite well to the hypotenuse. Seems like an interesting subject to elaborate on.

Hypotenuse = 7/8* base + height/2    

How is 7/8*base + height/2 somewhat equivalent to sqrt(a^2 + b^2)

Answer 1

Let the legs measure $a$ and $ka$ with $k>1$. Then the approximation given is:

$\frac{7ka}{8}+\frac{4a}{8}=\frac{(7k+4)a}{8}$.

The real measure is $\sqrt{k^2a^2+a^2}=\sqrt{k^2+1}a$.

So how does $\frac{7k+4}{8\sqrt{k^2+1}}$ behave? Not that bad.

Here is a graph:

So as the graph shows, in the interval $(1,\infty)$ the best approximation occurs at $k=1$ for which we get $\frac{7+4}{8\sqrt{2}}=\frac{11}{2\sqrt2}\approx 0.972$. After this the ratio becomes smaller and smaller, the limit is $\frac{7}{8}=0.875$.

Can this be improved? yes it can, the formula always gives us a length shorter than the actual length, so we can obtain a better aproximation by taking slightly larger coefficients.

A better question is which is the best aproximation for $\sqrt{a^2+b^2}$ that is of the form $la+mb+n$ with $l,m,n\in \mathbb Q$. Now, the value of $l$ is going to be irrelevant because when $a$ and $b$ are large enough the $l$ won't matter much.

So we need to approximate $\sqrt{a^2+b^2}$ with $la+mb$. If we write $b$ as $ka$ then we need to approximate $\sqrt{k^2+1}a$ with $l+mk(a)$. So essentially what we need to do is approximate $\sqrt{k^2+1}$ with $l+mk$. This is the real problem.

The approximation for $\sqrt{k^2+1}$ provided in the question is $\frac{7k+4}{8}$. Now, if we were to approximate $\sqrt{k^2+1}$ by $mk+l$ I would think it would be in our best interest to make $m=1$ (so that at least when $k$ goes to infinity the limit becomes $1$. Then it is only a matter of finding a good $l$.

I didn't think a lot but taking $l=\frac{3}{7}$ seems to give a good result. Here is the graph of $\frac{k+3/7}{\sqrt{k^2+1}}$

This is a better approximation, the ratio of the correct measurement, versus the actual measurement when $k\geq 1$ reaches a maximum of approximately $1.088$ when $k=2.\overline 3$, this is the worst it gets, it improves when $k$ approaches $1$, reaching the minimum of $1.01$ and it also improves as $k$ goes to infinity, with a limit of $1$. (as an opposite of the first approximation this approximation always gives a hypotenuse longer than it actually is, which again tells us this is not actually the best approximation)

So a better way to approximate the hypotenuse is to add the longer leg's length plus three sevenths of the shorter leg's length.

Answer 2

The method provides a not-so-great approximation when the two catheti are roughly of the same length. In this case, $$\frac{7}{8}a+\frac{1}{2}b\approx\frac{7}{8}a+\frac{1}{2}a=\frac{11}{8}a=1\mathrm.375 a\approx(1\mathrm.414...)a=\sqrt{2}{a}\approx\sqrt{a^2+b^2}.$$

Answer 3

Numerical optimization reveals how truly astonishing the approximation is:

Taking a hint from @dREaM's answer and normalizing the length of the shortest side, for side lengths $1$ and $k$ we are interested in the ratio

$$\frac{ak+b}{\sqrt{k^2+1}}$$

as a function of the coefficients $a$ and $b$ (in the Tamil approximation, $a=7/8$ and $b=1/2$). We want the ratio to be as close to $1$ as possible for a large number of side lengths. Some experimentation shows that it is the region $k \in [1,3]$ that is the most problematic, so it makes sense to minimize the integral

$$ \int_1^3 \left(1- \frac{ak+b}{\sqrt{k^2+1}}\right)^2 \>dk $$

for $a,b$. Numerically, the minimum lies near

$$ \begin{align} a &= 0.871079 \\ b &= 0.509221 \end{align} $$

which is very close to the values given in the original text. In fact, plotting the integrand for the original (orange) versus the numerically obtained (blue) coefficients shows that the values are very near optimal in the range $[1,3]$, and most of the discrepancy happens where the side lengths are close to each other (that is, where $k$ is close to $1$):

If we assume that most practical right triangles have short sides that are within a factor of $3$ of each other, then given the very simple fractions used there can be no doubt that the original approximation is "optimal" in a practical sense.

Answer 4

This is not an answer but it is too long for a comment.

Interested by pew's answer, I focused on $$I=\int_1^3 \left(1- \frac{ak+b}{\sqrt{k^2+1}}\right)^2 \>dk$$ Using a CAS, $$I=\frac{1}{4} a^2 \left(8+\pi -4 \tan ^{-1}(3)\right)+a \left(b \log (5)-2 \sqrt{2} \left(\sqrt{5}-1\right)\right)+b^2 \left(\tan ^{-1}(3)-\frac{\pi }{4}\right)+2 b \left(\sinh ^{-1}(1)-\sinh ^{-1}(3)\right)+2$$ Taking derivatives $$I'_a=\frac{1}{2} a \left(8+\pi -4 \tan ^{-1}(3)\right)+b \log (5)-2 \sqrt{2} \left(\sqrt{5}-1\right)$$ $$I'_b=a \log (5)+2 b \left(\tan ^{-1}(3)-\frac{\pi }{4}\right)+2 \left(\sinh ^{-1}(1)-\sinh ^{-1}(3)\right)$$ Setting the derivatives to zero and solving, we obtain easily the analytical expressions for $a$ anf $b$ (the numerical values of them are given in pew's answer). Their expressions are really ugly !

Answer 5

How is 7/8*base + height/2 somewhat equivalent to sqrt(a^2 + b^2)

This is simply a linear approximation of the Euclidean distance function on one octant of the plane by measuring the length of a scaled projection to the vector

$$\binom{\frac{7}{8}}{\frac{1}{2}} .$$

This works because a circle doesn't look that different from a straight line when it's observed over a sufficiently small angle, such as a single octant.

The figure below tries to demonstrate this; the black arc is the unit circle inside the octant, blue line corresponds to points at the unit distance measured by this projection, and the dashed blue arrow is the vector above.

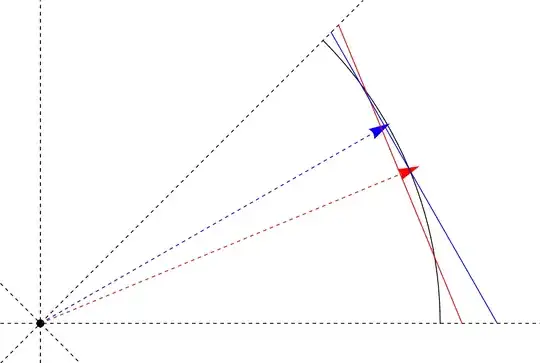
There are multiple criteria for these sort of approximations, but if we want to make the mean distance measure over all points in the octant match the Euclidean norm, the optimal vector is:

$$\frac{\pi}{8} \csc \left(\frac{\pi}{8}\right) \binom{\cos \left(\frac{\pi }{8}\right)}{\sin \left(\frac{\pi }{8}\right)} = \frac{\pi}{8} \binom{1+\sqrt{2}}{1}$$

... which corresponds with the red parts in the figure above. (Yes, I pulled this out of my Mathematica session.) These vectors are easier to compare as decimal approximations:

$$\binom{0.875}{0.5} vs. \binom{0.948059}{0.392699}$$

They're not that far off if you're using just multiplies of eighths and actually care about the situation also from the perspective of the length and the angle of the vector.

The "optimal" solution above also has a nice correspondence with a regular octagon overlapping the unit circle:

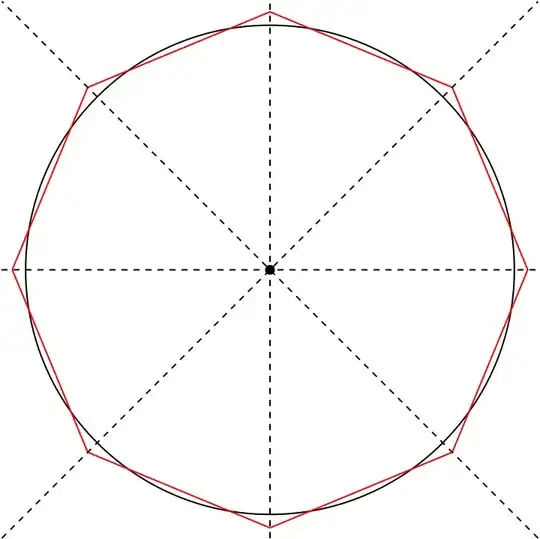
Here the red octagon corresponds to the above vector projection measure, extended over all octants. If maximum error of 5.2% and standard deviation of 2.3% over all points is fine by you, this is a sufficient replacement for the Euclidean norm.

Slightly different vectors result with differing criteria (although thanks to geometry, they all have the same direction). If one doesn't demand that mean measure over all points at a specific distance matches the Euclidean norm, there are multiple options. For instance, for the minimal maximum error measured in relative terms:

$$\frac{4}{2+\sqrt{2+\sqrt{2}}} \binom{\cos \left(\frac{\pi }{8}\right)}{\sin \left(\frac{\pi }{8}\right)} \approx \binom{0.960434}{0.397825}$$

One for the minimal maximum error measured by logarithm:

$$\sqrt[4]{4-2 \sqrt{2}} \binom{\cos \left(\frac{\pi }{8}\right)}{\sin \left(\frac{\pi }{8}\right)} \approx \binom{0.961187}{0.398136}$$

And one which minimises the standard error:

$$\frac{8 \sqrt{2-\sqrt{2}}}{2 \sqrt{2}+\pi } \binom{\cos \left(\frac{\pi }{8}\right)}{\sin \left(\frac{\pi }{8}\right)} \approx \binom{0.947544}{0.392485}$$

The benefit of the Indian approximation is the easy terms for manual calculation, but it's obviously worse in accuracy, especially the obvious 12.5% maximum error.

Answer 6

If we start with the following pythagorean triplet $$ m^2 + n^2 , m^2 - n^2 , 2mn$$ Then your method produces, $$ m^2+n^2=\frac{7}{8} \times(m^2-n^2)+mn$$ $$\frac{m^2}{8}+\frac{15}{8}\times n^2 - mn=0$$ $$m^2-8mn+15n^2=0$$ $$(m-3n)(m-5n)=0$$ So, the method above will work perfectly for above pythagorean triplets with m=3n or m=5n.

Answer 7

I am providing a simple method to compute Hypotenuse without computing square root. Take the longer side as A and smaller side as B.

If A >= B/2, then use the formula given above: Hypotenuse = 7/8* A + B/2

If A < B/2, then use the following formula: Hypotenuse = A + B^2/(2*A)

This should give a reasonably good estimate.

If you are looking for still better results, then use Hypotenuse = 0.81A + 0.6B if A and B are nearly equal.