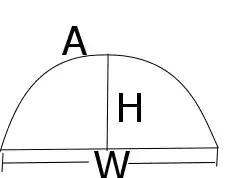
I am doing the curvature correction of the object boundary, I need to calcluate the maximum height perpendicular to the arc shown in the figure. I know the chord length and arc length, But i don't know the radius of the arc. I would like to know how to find out the maximum height perpendicular to the the arc if we have only two parameters like W and A. Please help me to solve this problem. Thanks in advance.
As Aretino answered, to solve for $\theta$ equation $$f(\theta)=\frac{\sin(\theta)} \theta-a=0$$ you will need a numerical method and Newton will probably be the simplest. Personally, I would prefer to consider $$g(\theta)=\sin(\theta)-a \theta=0$$ You could be interested by this post.
Using Newton method with a reasonable guess $\theta_0$, it will be updated according to
$$\theta_{n+1}=\theta_n-\frac{g(\theta_n)}{g'(x_n)}$$ which will then be $$\theta_{n+1}=\frac{\sin (\theta_n )-\theta_n \cos (\theta_n )}{a-\cos (\theta_n )}$$
For the starting guess, you could use the beautiful approximation $$\sin(\theta) \simeq \frac{16 (\pi -\theta) \theta}{5 \pi ^2-4 (\pi -\theta) \theta}\qquad (0\leq \theta\leq\pi)$$ proposed by Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician (have a look here). Solving the quadratic will give $$\theta_0= \frac{2 \sqrt{2 \pi a+4-\pi ^2 a^2}+\pi a-4}{2 a}$$ and Newton method would converge in very few iterations.
For illustration purposes, let us use $a=0.5$. The iterates will then be $$\left( \begin{array}{cc} n & \theta_n \\ 0 & 1.8947720683167907653 \\ 1 & 1.8954945691081046778 \\ 2 & 1.8954942670340337422 \\ 3 & 1.8954942670339809471 \end{array} \right)$$ which is the solution for $20$ significant figures.
Doing the same with $a=0.9$ would give $$\left( \begin{array}{cc} n & \theta_n \\ 0 & 0.78035069742025663946 \\ 1 & 0.78675773101028416327 \\ 2 & 0.78668308222856641907 \\ 3 & 0.78668307204921216197 \\ 4 & 0.78668307204921197269 \end{array} \right)$$
Doing the same with $a=0.1$ would give $$\left( \begin{array}{cc} n & \theta_n \\ 0 & 2.8537061060216672396 \\ 1 & 2.8523421443538252996 \\ 2 & 2.8523418944501000631 \\ 3 & 2.8523418944500916483 \end{array} \right)$$
Uou could also be interested by the Padé approximation $$\frac{\sin(\theta)} \theta\approx \frac{1-\frac{53 }{396}\theta^2+\frac{551 }{166320}\theta^4 } {1+\frac{13 }{396}\theta^2+\frac{5 }{11088} \theta^4}$$ which let you with a quadratic in $\theta^2$ for a final solution $$\theta= \sqrt{6} \sqrt{\frac{\sqrt{35} \sqrt{-3985 a^2+130862 a+25583}-455 a-1855}{75 a-551}}$$ For the worked examples, the values are $1.89552$, $0.786683$ and $2.85381$.
Similar to the Padé approximant, we also could write $$\frac{\sin(\theta)} \theta\approx \frac{1+a\theta^2+b\theta^4 } {1+c\theta^2+d\theta^4}$$ and impose that the values of the function, its first and second derivative be strictly identical at $\theta=0$ and $\theta=\pi$, we should have $$a=\frac{2}{\pi ^2}-\frac{1}{3}\qquad b=-\frac{1+\left(\frac{2}{\pi ^2}+\frac{1}{3}\right) \pi ^2}{\pi ^4}\qquad c=\frac{2}{\pi ^2}-\frac{1}{6}\qquad d=\frac{10-\pi ^2}{2 \pi ^4}$$ For the worked examples, the values are $1.89530$, $0.786645$ and $2.85232$.
If you just need a very crude estimate for starting Newton iterations, you could also use $$\frac{\sin(\theta)} \theta\approx \frac{1}{3} \left(1+2 \cos \left(\frac{2 \theta }{3}\right)\right)\implies \theta =\frac{3}{2} \cos ^{-1}\left(\frac{3 a-1}{2} \right)$$ For the worked examples, the values are $1.97717$, $0.832217$ and $2.89255$.
If $\theta$ is half the center angle (in radians) subtended by the arc ($0\le\theta\le\pi$), and $R$ the arc radius, then we have: $$ A=2R\theta,\quad W=2R\sin\theta,\quad \hbox{and}\quad H=R(1-\cos\theta). $$ Dividing the second equation by the first one gets $$ {\sin\theta\over\theta}={W\over A}, \quad\hbox{that is:}\quad \mathop{\rm{sinc}}\theta={W\over A}. $$ This equation has a unique solution $\theta\in(0,\pi)$, if $0<W/A<1$ (as it should be), but there is no commonly defined name for the inverse of the sinc function. The value of $\theta$ must then usually be found by some numerical method.
Once you find $\theta$, just plug it into the first equation to get $R$ and then use the third equation to find $H$.
Here's the simple solution you're looking for, but it's only an approximation, plus or minus 2 or 3%.
s=sagitta (or height), a=arc length, c=chord length
s = 0.42 * √( a^2 - c^2 )
c = √( a^2 - (s/0.42)^2 )
a = √( c^2 + (s/0.42)^2 )
If the arc is more like a full semi-circle (where radius=sagitta), then the constant will be a little closer to 0.4127. If the arc is more flat (very large radius), then the constant will be closer to 0.43. But these are minor differences for an approximation.
