Density of sum of two independent uniform random variables on $[0,1]$

Question

I am trying to understand an example from my textbook.

Let's say $Z = X + Y$, where $X$ and $Y$ are independent uniform random variables with range $[0,1]$. Then the PDF is $$f(z) = \begin{cases} z & \text{for $0 < z < 1$} \\ 2-z & \text{for $1 \le z < 2$} \\ 0 & \text{otherwise.} \end{cases}$$

How was this PDF obtained?

Thanks

Answer 1

If we want to use a convolution, let $f_X$ be the full density function of$X$, and let $f_Y$ be the full density function of $Y$. Let $Z=X+Y$. Then $$f_Z(z)=\int_{-\infty}^\infty f_X(x)f_Y(z-x)\,dx.$$

Now let us apply this general formula to our particular case. We will have $f_Z(z)=0$ for $z\lt 0$, and also for $z\ge 2$. Now we deal with the interval from $0$ to $2$. It is useful to break this down into two cases (i) $0\lt z\le 1$ and (ii) $1\lt z\lt 2$.

(i) The product $f_X(x)f_Y(z-x)$ is $1$ in some places, and $0$ elsewhere. We want to make sure we avoid calling it $1$ when it is $0$. In order to have $f_Y(z-x)=1$, we need $z-x\ge 0$, that is, $x\le z$. So for (i), we will be integrating from $x=0$ to $x=z$. And easily $$\int_0^z 1\,dx=z.$$ Thus $f_Z(z)=z$ for $0\lt z\le 1$.

(ii) Suppose that $1\lt z\lt 2$. In order to have $f_Y(z-x)$ to be $1$, we need $z-x\le 1$, that is, we need $x\ge z-1$. So for (ii) we integrate from $z-1$ to $1$. And easily $$\int_{z-1}^1 1\,dx=2-z.$$ Thus $f_Z(z)=2-z$ for $1\lt z\lt 2$.

Another way: (Sketch) We can go after the cdf $F_Z(z)$ of $Z$, and then differentiate. So we need to find $\Pr(Z\le z)$.

For a few fixed $z$ values, draw the lines with equation $x+y=z$ on an x-y axis plot. Draw the square $S$ with corners $(0,0)$, $(1,0)$, $(1,1)$, and $(0,1)$.

Then $\Pr(Z\le z)$ is the area of the part $S$ that is "below" the line $x+y=z$. That area can be calculated using basic geometry. For example, when z is 2, the whole square area is under the line so Pr=1. There is a switch in basic shape at $z=1$.

Answer 2

Here's why we need to break the convolution into cases. The integral we seek to evaluate for each $z$ is $$ f_Z(z):= \int_{-\infty}^\infty f(x)f(z-x)\,dx.\tag1 $$ (On the RHS of (1) I'm writing $f$ instead of $f_X$ and $f_Y$ since $X$ and $Y$ have the same density.) Here the density $f$ is the uniform density $f(x)$, which equals $1$ for $0<x<1$, and is zero otherwise. The integrand $f(x)f(z-x)$ will therefore have value either $1$ or $0$. Specifically, the integrand is $1$ when $$ 0<x<1\qquad\text{and}\qquad 0<z-x<1,\tag2 $$ and equals zero otherwise. To evaluate (1), which is an integral over $x$ (with $z$ held constant), we need to find the range of $x$-values where the conditions listed in (2) are satisfied. How does this range depend on $z$? Plotting the region defined by (2) in the $(x,z)$ plane, we find:

and it's clear how the limits of integration on $x$ depend on the value of $z$:

1. When $0<z<1$, the limits run from $x=0$ to $x=z$, so $f_Z(z)=\int_0^z 1dx=z.$

2. When $1<z<2$, the limits run from $x=z-1$ to $x=1$, so $f_Z(z)=\int_{z-1}^11dx=2-z.$

3. When $z<0$ or $z>2$, the integrand is zero, so $f_Z(z)=0$.

Answer 3

I provide a method here by using bivariate transformation. Let $X \sim Uniform(0,1)$ and $Y \sim Uniform(0,1)$. $X$ and $Y$ are independent. We want to know the density of $X+Y$.

Since X and Y are independent, then their joint distribution is \begin{equation} \begin{split} f_{X,Y}(x,y)&=f_X(x) f_Y(y) \\ &= \begin{cases} 1 &\text{if $0<x<1, 0<y<1$}\\ 0 &\text{otherwise} \end{cases} \end{split} \end{equation}

Now let $U=X+Y, V=X$. Thus $X=V=h_1(u,v), Y=U-V=h_2(u,v)$. It is easy to compute that $|J|=1$

Thus, \begin{equation} \begin{split} f_{U,V}(u,v) &= f_{X,Y}(h_1(u,v),h_2(u,v)) |J| \\ &= \begin{cases} 1 &\text{if $(u,v) \in \mathcal{B} $}\\ 0 &\text{otherwise} \end{cases} \end{split} \end{equation}

where $\mathcal{A}=\{(x,y):f_{X,Y}(x,y) >0\} $ and $\mathcal{B}=\{(u,v):u=g_1(x,y), v=g_2(x,y) \text{ for some $(x,y) \in \mathcal{A}$}\}$

We need to know what $\mathcal{B}$ is. Since $0<x<1,o<y<1$, this is equivalent to $0<v<1, 0<u-v<1$, also equivalent to $0<v<1, v<u<v+1$. Thus $\mathcal{B} = \{ (u,v): 0<v<1, v<u<v+1$ }

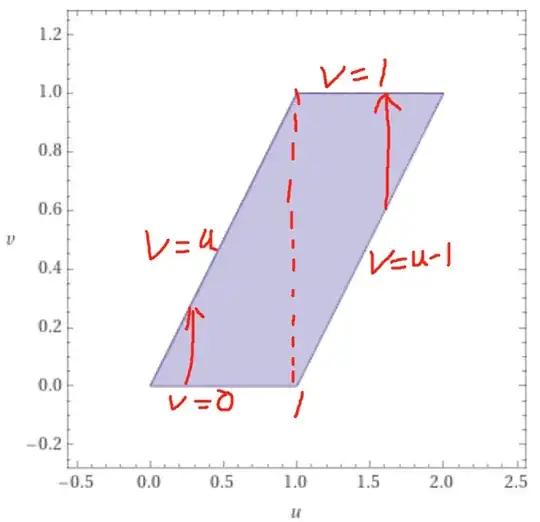
Then $f_U(u) = \int_{-\infty}^\infty f_{U,V}(u,v) dv=\int_\mathcal{B} f_{U,V}(u,v) dv=\int_\mathcal{B} 1 dv $

Notice that $0<v<1, v<u<v+1$ implies $0<u<2$. When $0<u<1$, v varies from 0 and u. Thus $\int_\mathcal{B} 1 dv = \int_0^u 1dv=u$. When $1<u<2$, v varies from $u-1$ and 1. Thus $\int_\mathcal{B} 1 dv = \int_{u-1}^1 1dv=2-u$. Together the result holds.

Answer 4

By the hint of jay-sun, consider this idea, if and only if $f_X (z-y) = 1$ when $0 \le z-y \le 1$. So we get

$$ z-1 \le y \le z $$

however, $z \in [0, 2]$, the range of $y$ may not be in the range of $[0, 1]$ in order to get $f_X (z-y) = 1$, and the value $1$ is a good splitting point. Because $z-1 \in [-1, 1]$.

Consider (i) if $z-1 \le 0$ then $ -1 \le z-1 \le 0$ that is $ z \in [0, 1]$, we get the range of $y \in [0, z]$ since $z \in [0, 1]$. And we get $\int_{-\infty}^{\infty}f_X(z-y)dy = \int_0^{z} 1 dy=z$ if $z \in [0, 1]$.

Consider (ii) if $z-1 \ge 0$ that is $ z \in [1, 2]$, so we get the range of $y \in [z-1, 1]$, and $\int_{-\infty}^{\infty}f_X(z-y)dy = \int_{z-1}^{1} 1 dy = 2-z$ if $z \in [1, 2]$.

To sum up, consider to clip the range in order to get $f_X (z-y) = 1$.

Answer 5

The purpose of this answer is to show how a direct application of convolution may lead to the desired result. I take the following results from Cohn, Measure Theory.

Definition of convolution Let $\nu_1$ and $\nu_2$ be finite measures on $(\mathbb{R}^d,\mathscr{B}(\mathbb{R}^d))$, then their convolution $\nu_1\ast\nu_2$ is defined by:

$$ \nu_1 \ast\nu_2(A) = \nu_1 \times\nu_2(\{(x_1,x_2) : x_1+x_2 \in A\})$$

Proposition 10.1.12 Let $\nu_1$ and $\nu_2$ be probability measures on $(\mathbb{R}^d,\mathscr{B}(\mathbb{R}^d))$.

$\vdots$

(c) If $\nu_1$ and $\nu_2$ are absolutely continuous, with densities $f$ and $g$, then $\nu_1\ast\nu_2$ is absolutely continuous with density: $$x \mapsto \int f(x-y)g(y)\lambda(dy)$$

Let $I$ denote the unit interval $[0,1]$, and $U(I)$ the uniform distrbution on $I$. Then the density function corresponding to $U(I)$ is $\chi_I$, the indicator function for $I$. If $X$ and $Y$ are independent random variables whose distributions are given by $U(I)$, then the density of their sum is given by the convolution of their distributions. I.e., if $f_X$ denotes the density for random variable $X$, then

$$ f_{X+Y}(x) = \int f_X(x-y)f_Y(y)\lambda(dy) = \int \chi_I(x-y)\chi_I(y) dy$$

The indicator function of $y$ alone restricts the integration range, so that

$$ \int \chi_I(x-y)\chi_I(y)dy = \int_0^1 \chi_I(x-y) dy$$

The expression $\chi_I(x-y)$ is $0$ if $x-y < 0$ or $x-y > 1$:

$$\chi_I(x-y) = \cases{1 & $x-1 \leq y \leq x$ \\ 0 & otw} $$

This further restricts the range of the integral, which can be rewritten:

$$\int_{max(0,x-1)}^{min(1,x)} 1 dy = min(1,x) - max(0,x-1)$$

The density is $0$ if $x < 0$ or $x > 2$. This fact is hidden in our final expression because we've expressed our indicator functions through the bounds of the integral, but can be recovered by including another indicator function. The PDF as described in the original question follows by considering the relevant cases.

Answer 6

Simple approach for those who don't know convolution.

First we need to find the range of possibilities for the sum.

• Minimum will occur when both numbers are minimum, so min = 0.
• Maximum will occur when both numbers are maximum, so max = 2.
• Most likely outcome (or mode) is when both numbers are same as their mean, so mode = 1.

These three are enough to specify a triangular distribution. We need to make sure that the area under the pdf is 1, which means the height of pdf at mode(h) is

$$ \frac{1}{2}*2*h = 1 $$

This gives $h=1$. All you need know is to find the equations of 2 lines that go from-

1. (0,0) to (1,1)
2. (1,1) to (2,0)

Give a shout if anything is not clear.

Answer 7

I know that this may be beyond what the OP wants, but there is way to directly compute the density of $\sum_{k=1}^{n}X_{k}$ when $X_{k}$s are i.i.d uniform over $[0,1]$, using Laplacian Transform.

Denote by $f$ the density of $X_{1}+\cdots+X_{n}$. Since $X_{k}$s are independent and identically distributed, we have $$\mathscr{L}\{f\}(s)=\mathbb{E}(e^{-s\sum_{k=1}^{n}X_{k}})=\prod_{k=1}^{n}\mathbb{E}(e^{-sX_{1}})=\prod_{k=1}^{n}\int_{0}^{1}e^{-sx}dx=\Big(\dfrac{1-e^{-s}}{s}\Big)^{n}.$$ Using binomial formula, we have \begin{align*} \Big(\dfrac{1-e^{-s}}{s}\Big)^{n}=\dfrac{1}{s^{n}}(1-e^{-s})^{n}&=\dfrac{1}{s^{n}}\sum_{k=0}^{n}{n\choose k}1^{n-k}(-e^{-s})^{k}\\ &=\sum_{k=0}^{n}{n\choose k}(-1)^{k}e^{-sk}s^{-n}.\\ \end{align*} Note that $e^{-sk}$ is the Laplace transform of $\delta_{k}$ where $\delta_{k}(x):=0$ when $x\neq k$ and $\delta_{k}(k):=1$, because $$\int_{0}^{\infty}e^{-sx}d\delta_{k}(x)=e^{-sk}.$$ On the other hand, note that $$s^{-n}=\dfrac{1}{s^{n}}=\dfrac{1}{(n-1)!}\dfrac{(n-1)!}{s^{n}}=\dfrac{1}{(n-1)!}\mathscr{L}\{x^{n-1}\}(s).$$ Set $g(x):=x^{n-1}$, we have $$e^{-sk}s^{-n}=\dfrac{1}{(n-1)!}\mathscr{L}\{g\}(s)\mathscr{L}\{\delta_{k}\}(s)=\dfrac{1}{(n-1)!}\mathscr{L}\{g*\delta_{k}\}(s).$$ Note that $$g*\delta_{k}(t)=\int_{0}^{t}g(t-u)\delta_{k}(u)du= \begin{cases} (t-k)^{n-1},\ \text{if}\ t\geq k\\ 0,\ \text{if}\ t<k \end{cases} :=(t-k)_{+}^{n-1}.$$

Combining computation, we derive \begin{align*} \mathscr{L}\{f\}(s)=\sum_{k=0}^{n}{n\choose k}(-1)^{k}e^{-sk}s^{-n}&=\sum_{k=0}^{n}{n\choose k}(-1)^{k}\dfrac{1}{(n-1)!}\mathscr{L}\{g*\delta_{k}\}(s)\\ &=\mathscr{L}\Big\{\sum_{k=0}^{n}{n\choose k}(-1)^{k}\dfrac{1}{(n-1)!}(t-k)_{+}^{n-1}\Big\}(s). \end{align*} Since the Laplacian transform is unique in the sense that if $\mathscr{L}\{f\}(s)=\mathscr{L}\{h\}(s)$ for all $s$, then $f=h$ (the condition is not exactly like this but it is sufficiently enough for our case), it then follows that \begin{equation*} f(t)=\sum_{k=0}^{n}{n\choose k}(-1)^{k}\dfrac{1}{(n-1)!}(t-k)_{+}^{n-1}. \end{equation*}