0

I know this very question has been discussed many times on SE here, here, here, here, and here, however after spending time looking over all of those posts, I am still struggling very much with understanding the basic concept, and am wondering if I am missing some fundamental introduction that is causing my lack of understanding. Here is the question:

Let $X$ and $Y$ be two independent random variables uniformly distributed on $[0, 1]$. Compute the probability density function of $X + Y$

The basic setup is

$$f_X(a) = f_Y (a) = \begin{cases} 1, & 0\le a\le1 \\ 0, & \text{otherwise} \end{cases}$$

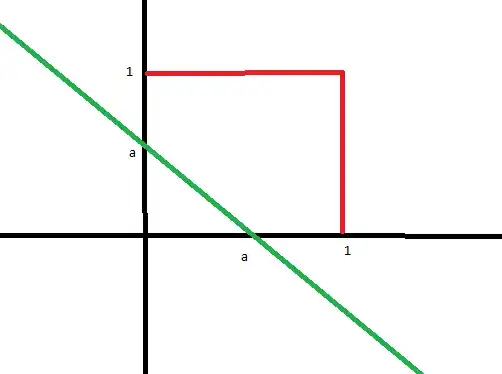
I would like to to first try go about doing it without using convolution, as André Nicholas recommends here. So I make a sketch:

enter image description here

Where the green line represents $x+y=a$

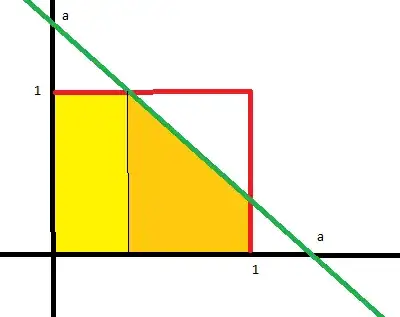
Now at this point I am confused where to put the green line. Does it make a difference if it is before $1$ or after $1$? If I put it after the $1$ would I have to calculate two different regions like this:

enter image description here

whereas if it is before the $1$ I only have to calculate one region? If so, how do I account for both possibilities?

Also, what do all the answers in those posts mean when they say you have to split up $a$ into two possibilities, one where $0\le a \le 1$ and one where $1\le a \le2$? Can somebody please explain to me in detail why that is necessary, what it actually means, if it can be illustrated in the diagram, and how exactly it expresses itself when setting up the integrals?

Also confusing is when I try to set up a double integral, I do not know how to do it correctly, possibly owing to my lack of understanding regarding the diagram. At first I thought I should do this:

$$P(X+Y \le a) = \int_0^1 \int_{0}^{a-y} \, dx \, dy $$

$$\int_0^1 (a-y)\,dy $$

$$a-{1\over2}$$

Which is incorrect. Somebody else also tried that here, and I don't understand the answer given there as to why these bounds are incorrect, or how to establish the correct bounds.

When I try

$$P(X+Y \le a) = \int_0^a \int_0^{a-y} \, dx \, dy$$

$$\int_0^a(a-y) \, dy $$

I get

$$a^2-{a^2\over2}$$

Which is also incorrect.

Do I need something along the lines of $$ = \int_0^{\min(1,a)}\int_0^{a-y} \, dx \, dy$$

If so, how do I go about doing that? I am not familiar with how to work with $\min, \max$ form in the bounds.

In summary, I am troubled by many things about this problem, and I am wondering if I am missing something very essential, which when I know it will provide with the key to understanding this and similar problems, and if somebody can identify what that is. Thank you very much.

Michael Hardy
  • 1
dlp
  • 935

1 Answers1

1

First let's just think geometrically. The behavior changes depending on whether $a<0,0<a \leq 1,1<a<2$ or $a \geq 2$:

  • $a \leq 0$: the area under the line doesn't overlap with the square at all.
  • $0<a \leq 1$: the area under the line overlaps with the square in a right triangle.
  • $1<a<2$: the area under the line overlaps with the square in a trapezoid. You can reduce this to the previous case by noting that the area above the line overlaps with the square in a triangle again.
  • $a \geq 2$: the area under the line contains the entire square.

Now returning to doing it symbolically. Your first attempt:

$$\int_0^1 \int_0^{a-y} \, dx \, dy$$

is on the right track, but it misses some things. First, when $0<a<1$, $y$ cannot go all the way up to $1$, it can only go up to $a$, so you get

$$\int_0^a \int_0^{a-y} dx dy.$$

Second, for $a>1$, your attempt is too big because it includes the white triangle at the top left of the figure. You can fix that by clamping the integral to the top of the square, as

$$\int_0^1 \int_0^{\min \{ 1,a-y \}} \, dx \, dy.$$

If you don't like how these two cases look different, you can force them to look the same by writing it as

$$\int_0^1 \int_0^{\max \{ 0,\min \{ 1,a-y \} \}} \,dx\, dy.$$

Michael Hardy
  • 1
Ian
  • 101,645
  • Thank you. How does one solve an integral with $min$ in the bounds? – dlp Sep 06 '18 at 16:21
  • @agblt Well, the first one is just the length, so you have $\int_0^1 \min { 1,a-y } dy$. To compute that, you need to determine in which piece of $[0,1]$ the min is $1$ and in which piece it is $a-y$, which is determined by whether $y<a-1$ or $y>a-1$. This is where the casework that was confusing you before comes into play. (This casework can't be entirely avoided, seeing as the final answer is a piecewise function.) – Ian Sep 06 '18 at 16:23
  • I am still having trouble with that last integral, would you be able to complete the computation? Its not the form of $\int_0^{a-1}dy +\int_{a-1}^{1}dy$ , is it? – dlp Sep 07 '18 at 14:49
  • @agblt For $a>1$ it is of that form, but one of the two integrals has an integrand different from $1$... – Ian Sep 07 '18 at 15:29
  • @ Ian ok so it seems that $\int_0^{a-1}dy +\int_{a-1}^{1} \ y \ dy$ works for $1 \le a \le 2$, what about $0 \le a \le 1$? $\int_0^1 \int_0^{a-y} , dx , dy$ still gives me $a-{1\over2}$ which is not correct... – dlp Sep 09 '18 at 11:44
  • @agblt You may notice that when $a<1$, there is some negative area being counted here, and you need to exclude that. I edited that into the answer. – Ian Sep 09 '18 at 13:46
  • Ok, I understand now. Thank you so much for all the help! – dlp Sep 09 '18 at 15:51
  • @ Ian sorry to bother you again, but you helped me so much with this problem... When using a convolution with this problem, would $\int_{\max {0, a-1}}^{\max {1,a}}, dy$ be a correct way of stating it? – dlp Sep 17 '18 at 17:05
  • @agblt Really in a convolution way of writing it, you should use indicator functions to start and then simplify, rather than going straight to variable limits. That is, the PDF $f_{X+Y}(z)$ is given by $\int_{-\infty}^\infty f_X(x) f_Y(z-x) dx$, where $f_X$ and $f_Y$ are both the indicator function of $[0,1]$. – Ian Sep 17 '18 at 17:07