0

The following is given: $$X,Y\ \textit{are independent}$$ $$X∼exp(1),Y∼exp(2)$$ $$Z=e^{−X}+e^{−2Y}$$ And I want to find: $$f_Z(1)=?$$ As a part of my solution I do the following: $$Z=U+V$$ where $$U=e^{−X},V=e^{−2Y}$$ Using one dimensional transformation we get: $$U∼Uni(0,1),V∼Uni(0,1)$$

Since we know that X,Y are independent we can assume the same for U,V.

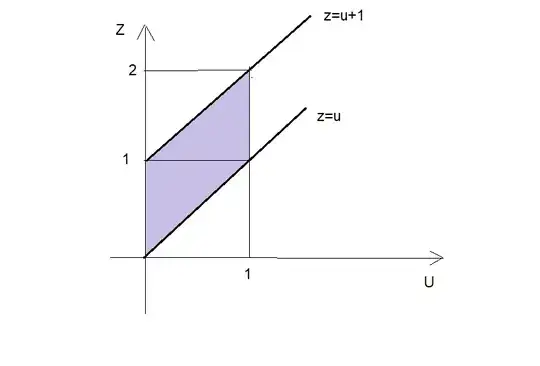
In order to calculate $f_Z$ im using a convolution integral : $$\int_{-\infty}^{\infty} f_U(u) \cdot f_V(z-u)du = \int_{0}^{1} 1 \cdot 1du = 1$$ According to the solution this is not $f_Z$, could you point out where I was wrong?

tommik
  • 32,733
  • 4
  • 15
  • 34
Eliran Turgeman
  • 183

2 Answers2

1

The mistake you are making is in thinking that $f_V(z-u)=1$ for all $u$ between $0$ and $1$. The value is $1$ only when $0<z-u<1$ or $z-1<u<z$. Split the calculation into the cases $z >2, z <0, 0<z<1$ and $1 <z<2$. I will post more details if you are unable to implement this.

The answer is $f_Z(z)=0$ if $z >2$ or $z <0$, $f_Z(z)=z$ if $0<z<1$ and $f_Z(z)=2-z$ if $ 1 <z<2$.

Kavi Rama Murthy
  • 311,013
  • I understand why $f_V(z-u) = 1$ only when $0<z-u<1$ or $z-1 <u<z$ But I don't fully understand why you split to these specific cases of $z$. Is it because $0<u<1$? – Eliran Turgeman Jul 15 '20 at 07:54
  • 1
    @EliranTurgeman $u$ has to satisfy two conditions: $0<u<1$ and $z-1 <u<z$. So we have to find the points common to the intervals $(0,1)$ and $(z-1,z)$. The intersection of these intervals is empty if $z>2$ or $z<0$ , it is $(0,z)$ if $0<z<1$ and $(z-1,1)$ if $1<z<2$. Try to plot these points on the real line to understand this. – Kavi Rama Murthy Jul 15 '20 at 07:59
1

a simple way to see the solution is to observe that

$$v=z-u$$

thus

$$0<z-u<1$$

this means that the joint density $f_{ZU}(z,u)$ is Uniformly distribuited over this parallelogram

enter image description here

Thus to get the marginal $f_Z$ it is enough to integrate in $du$

tommik
  • 32,733
  • 4
  • 15
  • 34