The answer included in CDF of two variable has been now edited and corrected by the author. The following is valid for a sum of two uniformly distributed continuous random variables:
$$\mathsf P(X+Y\leq z) = \begin{cases} 0 & : z< 0 \\[2ex] \int\limits_{0}^{z}\;\int\limits_{0}^{z-x} f_{X,Y}(x,y)\operatorname d y\operatorname d x & : 0 \leq z \leq 1 \\[2ex] \int\limits_{0}^{z-1}\;\int\limits_{0}^{1} f_{X,Y}(x,y)\operatorname d y\operatorname d x + \int\limits_{z-1}^{1}\;\int\limits_0^{z-x} f_{X,Y}(x,y)\operatorname d y\operatorname d x & : 1 < z \leq 2 \\[1ex] 1 & : 2 < z\end{cases}$$
where the outer integral is over $x$ variable. Let's explain the integration domain. It can be represented by $E\times F$ where both $E$ and $F$ are subsets of $[0,1]$. $F=[0,\min(z-x,1)]$ because $y\leq z-x\,\, \forall z$ and x.
To find $E$, it is suitable to split the unit interval depending on the value of z.
$0 \leq z \leq 1$:
$E=[0,z]\cup [z,1]$. However $x\in[z,1]$ does not fulfill the main $y\leq z-x$. Therefore $E=[0,z]$.
$1 < z \leq 2$:
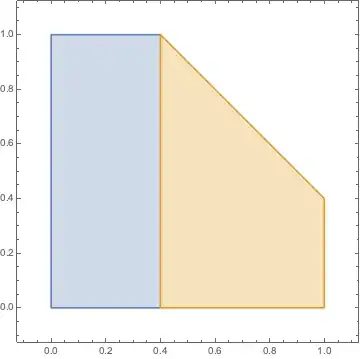
$E=[0,z-1]\cup [z-1,1]$.
$x \in[0,z-1]\implies \min(z-x,1)=1 \implies F=[0,1]$
$x \in [z-1,1] \implies \min(z-x,1)=z-x \implies F=[0,z-x]$
Example picture for the sum of two integrals in the region $1 < z \leq 2$ (for $z =1.4$):

\begin{align} P(X+Y\le z)&=\iint_{x+y,\le, z}\mathbf1_{0<x<1,0<y<1},dy,dx \&=\int_0^{\min(z,1)}\int_0^{\min(z-x,1)},dy,dx \&=\int_0^{\min(z,1)}\min(z-x,1),dx \&=\begin{cases}\int_0^z\min(z-x,1),dx&,\text{ if }0\le z<1\\int_0^1\min(z-x,1),dx&,\text{ if }1\le z<2\end{cases} \end{align}
– StubbornAtom Aug 03 '18 at 16:54