Density of sum of two uniform random variables

Question

I have two uniform random varibles. $X$ is uniform over $[\frac{1}{2},1]$ and $Y$ is uniform over $[0,1]$. I want to find the density funciton for $Z=X+Y$. There are many solutions to this on this site where the two variables have the same range (density of sum of two uniform random variables $[0,1]$) but I don't understand how to translate them to the case where one variable have a different range. Here's what I tried:

$$f_Z(z)=\int_{-\infty}^\infty f_X(x)f_Y(z-x)\,dx.$$

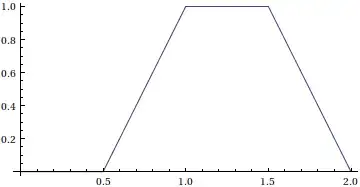
We will have $f_Z(z)=0$ for $z\lt \frac{1}{2}$, and also for $z\ge 2$. Two cases (i) $\frac{1}{2}\lt z\le 1$ and (ii) $1\lt z\lt 2$.

(i) In order to have $f_Y(z-x)=1$, we need $z-x\ge 0$, that is, $x\le z$. So for (i), we will be integrating from $x=\frac{1}{2}$ to $x=z$. $$f_Z(z)=\int_\frac{1}{2}^z 2 * 1\,dx=2z-1.$$ for $\frac{1}{2}\lt z\le 1$.

(ii) Suppose that $1\lt z\lt 2$. In order to have $f_Y(z-x)$ to be $1$, we need $z-x\le 1$, that is, we need $x\ge z-1$. $$f_Z(z)=\int_{z-1}^1 2*1\,dx=4-2z.$$ for $1\lt z\lt 2$.

For $z=1$ these two cases give different results, which doesn't make sense to me. Is there something wrong? How do I know which integration limits to use?

Answer 1

You have: $$f_Z(x)=(f_X*f_Y)(x)=\int_{-\infty}^{+\infty}2\cdot \mathbb{1}_{(1/2,1)}(y)\cdot\mathbb{1}_{(0,1)}(x-y)\,dy,$$ where $\mathbb{1}_J$ is the function that equals $1$ over $J$ and zero elsewhere. This can be written as: $$f_Z(x) = 2\int_{1/2}^{1}\mathbb{1}_{(0,1)}(x-y)dy $$ hence $f_Z$ is supported on $\left(\frac{1}{2},2\right)=\operatorname{Supp}(f_X)+\operatorname{Supp}(f_Y)$ and: $$f_Z(x)=\left\{\begin{array}{rcl}2x-1&\text{if}&x\in[1/2,1],\\1&\text{if}&x\in[1,3/2],\\4-2x&\text{if}&x\in[3/2,2],\\0&&\text{elsewhere,}\end{array}\right.$$ whose graphics is:

$\hskip2in$

Answer 2

As in Jack's answer, there are $3$ cases, not $2$.

$\frac{1}{2} \leq z \leq 1$:

$$f_Z(z) = \int_{1/2}^{z} 2\cdot1 \,dy = \bigg[2y\bigg]_{1/2}^{z} = 2z-1 $$

$1 \leq z \leq \frac{3}{2}$:

$$f_Z(z) = \int_{1/2}^{1} 2\cdot1 \,dy = \bigg[2y\bigg]_{1/2}^{1} = 2 - 1 =1 $$

$\frac{3}{2} \leq z \leq 2$:

$$f_Z(z) = \int_{z-1}^{1} 2\cdot1 \,dy = \bigg[2y\bigg]_{z-1}^{1} = 2 - \left(2z-2\right) = 4-2z $$

Your only real problem is the $z-1$ lower limit in your Case (ii). For $1 \leq z \lt \frac{3}{2}$ it puts $x \lt \frac{1}{2}$ which is invalid. Hence the need for the extra case.

For the sake of exercise, we could instead choose $y$ first and integrate over it, setting $x = z-y$:

$$f_Z(z)=\int_{-\infty}^\infty f_Y(y)f_X(z-y)\,dy.$$

$\frac{1}{2} \leq z \leq 1$:

$$f_Z(z) = \int_{0}^{z-1/2} 2\cdot1 \,dy = \bigg[2y\bigg]_{0}^{z-1/2} = 2z-1 $$

$1 \leq z \leq \frac{3}{2}$:

$$f_Z(z) = \int_{z-1}^{z-1/2} 2\cdot1 \,dy = \bigg[2y\bigg]_{z-1}^{z-1/2} = \left(2z-1\right) - \left(2z-2\right) =1 $$

$\frac{3}{2} \leq z \leq 2$:

$$f_Z(z) = \int_{z-1}^{1} 2\cdot1 \,dy = \bigg[2y\bigg]_{z-1}^{1} = 2 - \left(2z-2\right) = 4-2z $$

Of course, it's the same result as above for $f_Z(z)$. (And the same as Jack's answer.)