1

A question in my assignment asks:

Suppose that $X$ and $Y$ are independent with a common uniform distribution over $(0,1)$. Find the probability distribution function of $X+Y$.

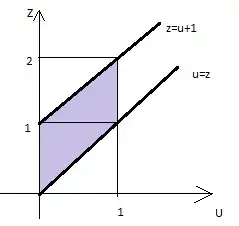
First I assume that I have a variable $a$ such that $a = X + Y$, and $ 0 < a <2$. I can then formulate the following:

$$f_{X+Y}(a) = \int^\infty_{-\infty} f_X(a-y)f_Y(y)dy$$

So far so good, mostly just putting in formula. Now I'm stuck. A quick reference to the answer key tells me that the above is also:

$$=\int^1_0f_X(a-y)\times1dy \\=\int^1_0f_X(a-y)dy$$

Can someone kindly explain the logic between the jump of converting the $(-\infty, \infty)$ to $(1,0)$, then assuming $f_Y(y) = 1$? How does that work, and does it have anything to do with the fact that I'm integrating w.r.t. $y$?

Thank you in advance!

a9302c
  • 349

2 Answers2

2

This is due to the fact that the support of the uniform joint distribution is $[0;1]\times [0;1]$

Instead of using directly the convolution you can use the jacobian thus you can appreciate the underlying logic.

to do that, set

$$\begin{cases} z=x+y \\ u=x \end{cases}\rightarrow \begin{cases} x=u \\ y=z-u \end{cases}$$

the jacobian is evidently $|J|=1$ thus

$$f_{UZ}(u,z)=1$$

Now observe that it must be

$$0<y<1$$

that is

$$0<z-u<1$$

which implies that the joint support is the following purple area

enter image description here

now I think it is evident that, in order to find the marginal $f_Z(z)$ you have to integrate in $du$ and thus,

if $0<z<1$ you get

$$f_Z(z)=\int_0^z du=z$$

while if $1<z<2$ you get

$$f_Z(z)=\int_{z-1}^{1}du=2-z$$

The result is a triangular density

tommik
  • 32,733
  • 4
  • 15
  • 34
1

The main thing to remeber here is that the probability density function of a uniform distribution is $$f_X(x) = \frac{1}{A-B} = \frac{1}{1} = 1$$

You might immediately ask "doesn't that mean that every point is certain?" and the answer is no because if you integrate around successively smaller intervals around the point you'll converge to 0.

Okay, so now we have that, but the next step is the integration limits. We'll do this: $$ \int\limits_{-\infty}^\infty f_X(a-y)f_Y(y) = \int\limits_{-\infty}^0 f_X(a-y)f_Y(y) + \int\limits_{0}^1 f_X(a-y)f_Y(y) + \int\limits_1^\infty f_X(a-y)f_Y(y) $$

Well, we know $f_Y(x) = 0$ if $x \not\in [0,1]$ so the outer two integrals vanish and we get

$$ \int\limits_{-\infty}^\infty f_X(a-y)f_Y(y) =\int\limits_{0}^1 f_X(a-y)f_Y(y) $$

Juan Sebastian Lozano
  • 2,704