Why does the series $\sum_{n=1}^\infty\frac1n$ not converge?

Question

Can someone give a simple explanation as to why the harmonic series

$$\sum_{n=1}^\infty\frac1n=\frac 1 1 + \frac 12 + \frac 13 + \cdots $$

doesn't converge, on the other hand it grows very slowly?

I'd prefer an easily comprehensible explanation rather than a rigorous proof regularly found in undergraduate textbooks.

Answer 1

Let's group the terms as follows:

Group $1$ : $\displaystyle\frac11\qquad$ ($1$ term)

Group $2$ : $\displaystyle\frac12+\frac13\qquad$($2$ terms)

Group $3$ : $\displaystyle\frac14+\frac15+\frac16+\frac17\qquad$($4$ terms)

Group $4$ : $\displaystyle\frac18+\frac19+\cdots+\frac1{15}\qquad$ ($8$ terms)

$\quad\vdots$

In general, group $n$ contains $2^{n-1}$ terms. But also, notice that the smallest element in group $n$ is larger than $\dfrac1{2^n}$. For example all elements in group $2$ are larger than $\dfrac1{2^2}$. So the sum of the terms in each group is larger than $2^{n-1} \cdot \dfrac1{2^n} = \dfrac1{2}$. Since there are infinitely many groups, and the sum in each group is larger than $\dfrac1{2}$, it follows that the total sum is infinite.

This proof is often attributed to Nicole Oresme.

Answer 2

There is a fantastic collection of $20$ different proofs that this series diverges. I recommend you read it (it can be found here). I especially like proof $14$, which appeals to triangular numbers for a sort of cameo role.

---

EDIT

It seems the original link is broken, due to the author moving to his own site. So I followed up and found the new link. In addition, the author has an extended addendum, bringing the total number of proofs to 42+.

Answer 3

This was bumped, so I'll add a proof sweet proof I saw in this site. Exponentiate $H_n$ and get $$e^{H_n}=\prod_{k=1}^n e^{1/k}\gt\prod_{k=1}^n\left(1+\frac{1}{k}\right)=n+1.$$ Therefore, $H_n\gt\log(n+1)$, so we are done. We used $e^x\gt1+x$ and telescoped the resulting product.

Answer 4

The answer given by AgCl is a classic one. And possibly pedagogically best; I don't know.

I also like the following argument. I'm not sure what students who are new to the topic will think about it.

Suppose 1 + 1/2 + 1/3 + 1/4 + ... adds up to some finite total S. Now group terms in the following way:

$$1 + \frac{1}{2} > \frac{1}{2} + \frac{1}{2} = \frac{2}{2} = 1$$

$$\frac{1}{3} + \frac{1}{4} > \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$$

$$\frac{1}{5} + \frac{1}{6} > \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$$

Continuing in this way, we get $S > S$, a contradiction.

Answer 5

An alternative proof (translated and adapted from this comment by Filipe Oliveira, in Portuguese, posted also here). Let $ f(x)=\ln(1+x)$. Then $f'(x)=\dfrac {1}{1+x}$ and $ f'(0)=1$. Hence

$$\displaystyle\lim_{x\to 0}\dfrac{\ln(1+x)}{x}=\lim_{x\to 0}\dfrac{\ln(1+x)-\ln(1)}{x-0}=1,$$

and

$$ \displaystyle\lim_{n\to\infty} \dfrac{\ln\left(1+\dfrac{1}{n}\right)}{\dfrac {1}{n}}=1>0.$$

So, the series $\displaystyle\sum\dfrac{1}{n}$ and $\displaystyle\sum\ln\left(1+\dfrac {1}{n}\right)$ are both convergent or divergent. Since

$$\ln\left(1+\dfrac {1}{n}\right)=\ln\left(\dfrac{n+1}{n}\right)=\ln (n+1)-\ln(n),$$

we have

$$\displaystyle\sum_{n=1}^N\ln\left(1+\dfrac {1}{n}\right)=\ln(N+1)-\ln(1)=\ln(N+1).$$

Thus $\displaystyle\sum_{n=1}^{\infty}\ln\left(1+\dfrac {1}{n}\right)$ is divergent and so is $\displaystyle\sum_{n=1}^{\infty}\dfrac{1}{n}$.

Answer 6

Let's group the terms as follows:$$A=\frac11+\frac12+\frac13+\frac14+\cdots\\ $$ $$ A=\underbrace{(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{9})}_{\color{red} {9- terms}} +\underbrace{(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\cdots+\frac{1}{99})}_{\color{red} {90- terms}}\\+\underbrace{(\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+\cdots+\frac{1}{999})}_{\color{red} {900- terms}}+\cdots \\ \to $$ $$\\A>9 \times(\frac{1}{10})+(99-10+1)\times \frac{1}{100}+(999-100+1)\times \frac{1}{1000}+... \\A>\frac{9}{10}+\frac{90}{100}+\frac{90}{100}+\frac{900}{1000}+...\\ \to A>\underbrace{\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+\frac{9}{10}+...}_{\color{red} {\text{ m group} ,\text{ and} \space m\to \infty}} \to \infty $$

Showing that $A$ diverges by grouping numbers.

Answer 7

This is not as good an answer as AgCl's, nonetheless people may find it interesting.

If you're used to calculus then you might notice that the sum $$ 1+\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n}$$ is very close to the integral from $1$ to $n$ of $\frac{1}{x}$. This definite integral is ln(n), so you should expect $1+\frac{1}{2}+\frac{1}{3}+\dots+ \frac{1}{n}$ to grow like $\ln(n)$.

Although this argument can be made rigorous, it's still unsatisfying because it depends on the fact that the derivative of $\ln(x)$ is $\frac{1}{x}$, which is probably harder than the original question. Nonetheless it does illustrate a good general heuristic for quickly determining how sums behave if you already know calculus.

Answer 8

Another interesting proof is based upon one of the consequences of the Lagrange's theorem applied on $\ln(x)$ function, namely:

$$\frac{1}{k+1} < \ln(k+1)-\ln(k)<\frac{1}{k} \space , \space k\in\mathbb{N} ,\space k>0$$

Taking $k=1,2,...,n$ values to the inequality and then summing all relations, we get the required result.

The proof is complete.

Answer 9

There also exists a proof for the divergence of the harmonic series that involves the Integral Test. It goes as follows.

It is possible to prove that the harmonic series diverges by comparing its sum with an improper integral. Specifically, consider the arrangement of rectangles shown in the figure of $ y = \dfrac {1}{x} $:

Each rectangle is $1$ unit wide and $\frac{1}{n}$ units high, so the total area of the rectangles is the sum of the harmonic series: $$ \displaystyle\sum \left( \text {enclosed rectangle are} \right) = \displaystyle\sum_{k=1}^{\infty} \dfrac {1}{k}. $$Now, the total area under the curve is given by $$ \displaystyle\int_{1}^{\infty} \dfrac {\mathrm{d}x}{x} = \infty. $$Since this area is entirely contained within the rectangles, the total area of the rectangles must be infinite as well. More precisely, this proves that $$ \displaystyle\sum_{n=1}^{k} \dfrac {1}{n} > \displaystyle\int_{1}^{k+1} \dfrac {\mathrm{d}x}{x} = \ln (k+1). $$This is the backbone of what we know today as the integral test.

Interestingly, the alternating harmonic series does converge: $$ \displaystyle\sum_{n=1}^{\infty} \dfrac {(-1)^n}{n} = \ln 2. $$And so does the $p$-harmonic series with $p>1$.

Answer 10

Let's assume that $\sum_{n=1}^{\infty}\frac1n=:H\in \mathbb{R}$, then $$H=\frac11+\frac12+\frac13+\frac14+\frac15+\frac16 +\ldots $$ $$H\geqslant \frac11+\frac12 +\frac14+\frac14+\frac16+\frac16+\ldots$$ $$H\geqslant \frac11+\frac12+\frac12+\frac13+\frac14+\frac15+\ldots$$ $$H\geqslant \frac12 +H \Rightarrow 0\geqslant \frac12$$ Since the last inequality doesn't hold, we can conclude that the sum doesn't converge.

Answer 11

Suppose to the contrary that converges.

Let $s_n$ denote the $n$-th partial sum. Since the serie converges, $(s_n)$ is a Cauchy sequence. Let $\varepsilon = 1/3$, then there is some $n_0$ such that $|s_q-s_p|< 1/3$ for all $q>p\ge n_0$. Let $q=2n_0$ and $p=n_0$. Then

$$\frac{1}{3}>\bigg|\sum_{n=n_0+1}^{2n_0} \frac{1}{n}\bigg|\ge\bigg|\sum_{n=n_0+1}^{2n_0} \frac{1}{2n_0}\bigg|=\frac{1}{2}$$

a contradiction. Then this contradiction shows that the series diverges.

Answer 12

$$\int_{0}^{\infty}e^{-nx}dx=\frac1n$$

$$\sum_{n=1}^{\infty}\int_{0}^{\infty}e^{-nx}dx=\lim_{ m \to \infty}\sum_{n=1}^{m}\frac1n$$

using the law of Geometric series

$$\int_{0}^{\infty}(\frac{1}{1-e^{-x}}-1)dx=\lim_{ m \to \infty}H_m$$

$$\lim_{ m \to \infty}H_m=\left [ \ln(e^x-1)-x \right ]_0^{\infty}\to\infty$$

Answer 13

Another (different) answer, by the Cauchy Condensation Test :

$$\sum_{n=1}^\infty \frac{1}{n} < \infty \iff \sum_{n=1}^\infty 2^n \frac{1}{2^n} = \sum_{n=1}^\infty 1< \infty $$

The latter is obviously divergent, therefore the former diverges. This is THE shortest proof there is.

Answer 14

Another answer that's very similar to others. But it's prettier, and perhaps easier to understand for the 9-th grade student who asked the same question here.

The student's question was ... does the sum equal some number $S$. But, look:

So, whatever it is, $S$ is larger than the sum of the infinite string of $\tfrac12$'s shown in the last line. No number can be this large, so $S$ can't be equal to any number. Mathematicians say that the series "diverges to infinity".

Answer 15

A non-rigorous explanation I thought of once: consider a savings scheme where you put a dollar in your piggy bank every day. So after $n$ days, you have $n$ dollars; clearly, your savings approach infinity. On the other hand, each day you add an additional $1/n$ proportion of your existing savings, "so" (the non-rigorous step) the accumulated percentage after $n$ days is $1 + 1/2 + \cdots + 1/n$.

This can be made rigorous through the infinite product argument $$\prod_{n = 1}^\infty (1 + \tfrac{1}{n}) < \infty \iff \sum_{n = 1}^\infty \frac{1}{n} < \infty$$ which is obtained, essentially, by taking the logarithm of the left-hand side and using the power series for $\log (1 + x)$.

Answer 16

I think the integral test gives the most intuitive explanation. Observe that $$\int^n_1 \frac1x dx= \log n$$ The sum $\displaystyle\sum^n_{k=1}\frac1k$ can be viewed as the area of $n$ rectangles of height $\frac1k$, width $1$ (with the first one having it's left hand side on the y axis, and all having their bottom on the x axis). The graph of $x\mapsto \frac1x$ can be drawn under these, so the sum will grow with $n$ at (least) as fast as the integral - hence will grow (at least) logarithmically.

Answer 17

The proof I learned, in Rosenlicht's Introduction to Analysis, published by Dover, is essentially a variant of the most popular answers above.

Namely, we will show that the sequence $S_n=\sum_{k=1}^n \dfrac 1k$ is not Cauchy.

For given $N\gt0$, look at $\vert S_{2N}-S_N\vert=\dfrac1{2N}+\dots+\dfrac 1{N+1}\ge N\cdot \dfrac 1{2N}=\dfrac 12$.

Answer 18

Let be the partial sum $H_n = \frac11 + \frac12 + \frac13 + \cdots + \frac1n$. Using Cesàro-Stolz: $$ \lim_{n\to\infty}\frac{H_n}{\log n} = \lim_{n\to\infty}\frac{H_{n+1}-H_n}{\log(n+1)-\log n} = \lim_{n\to\infty}\frac{\frac1{n+1}}{\log(1+1/n)} = \lim_{n\to\infty}\frac{\frac1{n+1}}{\frac1n} = 1 $$ and $$\sum_{n=1}^\infty\frac1n = \lim_{n\to\infty}H_n = \infty.$$

Answer 19

Visualize the harmonic series as the area of a sequence of rectangles: $$ S:=1+\frac12+\frac13+\frac14+\frac15+\cdots$$ Now compute this same area using horizontal rectangles: $$ \begin{align} \textstyle S=\sum\text{width $\cdot$ height} &= 1\cdot\left(1-\frac12\right) + 2\cdot\left(\frac12-\frac13\right) + 3\cdot\left(\frac13-\frac14\right) + 4\cdot\left(\frac14-\frac15\right)+\cdots\\ &=\left(1-\frac12\right)+\left(1-\frac23\right)+\left(1-\frac34\right)+\left(1-\frac45\right)+\cdots\\ &=\frac12+\frac13+\frac14+\frac15+\cdots \end{align} $$ ... and the first term in the sum has disappeared! Since $S=S-1$, the sum cannot be finite.

---

Here's the same argument as a one-liner: $$ \sum_{n=1}^\infty\frac1n\stackrel{(a)}= \sum_{n=1}^\infty\sum_{k=n}^\infty\left[\frac1k-\frac1{k+1}\right] =\sum_{n=1}^\infty\sum_{k=n}^\infty\frac1{k(k+1)} \stackrel{(b)}= \sum_{k=1}^\infty\sum_{n=1}^k\frac1{k(k+1)}=\sum_{k=1}^\infty\frac1{k+1} $$ In (a) we have a telescoping sum; in (b) the interchange in the order of summation is legal since all terms are nonnegative.

Answer 20

Using Euler's form of the Harmonic numbers,

$$\sum_{k=1}^n\frac1k=\int_0^1\frac{1-x^n}{1-x}dx$$

$$\begin{align} \lim_{n\to\infty}\sum_{k=1}^n\frac1k & =\lim_{n\to\infty}\int_0^1\frac{1-x^n}{1-x}dx \\ & =\int_0^1\frac1{1-x}dx \\ & =\left.\lim_{p\to1^+}-\ln(1-x)\right]_0^p \\ & \to+\infty \end{align}$$

---

Using the Taylor expansion of $\ln(1-x)$,

$$-\ln(1-x)=x+\frac{x^2}2+\frac{x^3}3+\frac{x^4}4+\dots$$

$$-\ln(1-1)=1+\frac12+\frac13+\frac14+\dots\quad\ $$

---

Using Euler's relationship between the Riemann zeta function and the Dirichlet eta function,

$$\begin{align} \sum_{k=1}^\infty\frac1{k^s} & =\frac1{1-2^{1-s}}\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k^s} \\ \sum_{k=1}^\infty\frac1k & =\frac10\sum_{k=1}^\infty\frac{(-1)^{k+1}}k\tag{$s=1$} \\ & \to+\infty \end{align}$$

Answer 21

One of the possible answers.

Firstly:

$$ \sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=\sum_{n=1}^{\infty}\frac{1}{(2n-1)2n} = \frac1{2}+\frac1{12}+\sum_{n=3}^{\infty}\frac{1}{(2n-1)2n} > \frac{1}{2}$$

Since $\displaystyle H_m = \sum_{n=1}^{m}\frac{1}{n}$ is increasing, if it is bounded, it converges, otherwise diverges to infinity.

Assume it converges, then:

$$\sum_{n=1}^{\infty}\frac{1}{n} = 2\frac{1}{2}+2\frac{1}{4}+2\frac{1}{6}+...+\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n} = \sum_{n=1}^{\infty}\frac{1}{n} + \sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}$$

which would be giving

$$\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}=0$$

and that is not the case.

Answer 22

We all know that $$\sum_{n=1}^\infty\frac1n=\frac 1 1 + \frac 12 + \frac 13 + \cdots $$ diverges and grows very slowly!! I have seen many proofs of the result but recently found the following: $$S =\frac 1 1 + \frac 12 + \frac 13 +\frac 14+ \frac 15+ \frac 16+ \cdots$$ $$> \frac 12+\frac 12+ \frac 14+ \frac 14+ \frac 16+ \frac 16+ \cdots =\frac 1 1 + \frac 12 + \frac 13 +\cdots = S.$$ In this way we see that $S > S$.

Answer 23

\begin{align} \sum_{n=1}^\infty\frac1n=\sum_{n=1}^\infty \int_0^1x^{n-1}\ dx=\int_0^1\sum_{n=1}^\infty x^{n-1}\ dx=\int_0^1\frac{dx}{1-x}=\int_0^1\frac{dx}{x}=\ln(1)-\ln(0)=\infty \end{align}

Answer 24

This is based on the same idea as several other answers, but the presentation, I think, is sufficiently different to make it worth adding. The key is to note that the inequalities $2\gt1$, $2/3\gt1/2$, and $2/5\gt1/3$ generalize to $2/(2n-1)\gt1/n$.

Let

$$S=1+{1\over2}+{1\over3}+{1\over4}+{1\over5}+{1\over6}+\cdots$$

If $S$ were finite then we would have

$$\begin{align} 2S&=2+{2\over2}+{2\over3}+{2\over4}+{2\over5}+{2\over6}+\cdots\\ &=\left(2+{2\over3}+{2\over5}+\cdots \right)+\left({2\over2}+{2\over4}+{2\over6}+\cdots \right)\\ &\gt\left(1+{1\over2}+{1\over3}+\cdots \right)+\left(1+{1\over2}+{1\over3}+\cdots \right)\\ &=2S \end{align}$$

But the strict inequality $2S\gt2S$ is impossible. So $S$ cannot be finite.

Answer 25

Let $r=\frac{m}{n}$ be any positive rational number. Beginning with the equation

$$ r=\underbrace{\frac{1}{n}+\frac{1}{n}+\dots+\frac{1}{n}}_{m\text{ times}} $$

and repeatedly applying the algebraic identity

$$ \frac{1}{p}=\frac{1}{p+1}+\frac{1}{p(p+1)} $$

we can eventually find an Egyptian fraction representation

$$r=\frac{1}{n_1}+\frac{1}{n_2}+\dots+\frac{1}{n_k}$$

of $r$ with $n_1<n_2<\dots<n_k$. So $r<H_{n_k}$.

Since $r$ was arbitrary, it follows that the sequence of harmonic numbers is unbounded. Thus the harmonic series diverges.

(I think the greedy algorithm for constructing Egyptian fractions doesn't work here, as you already need to know that the harmonic series diverges in order to prove that the greedy algorithm works for arbitrarily large rationals...)

Answer 26

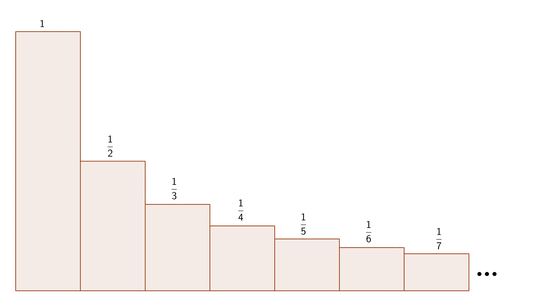
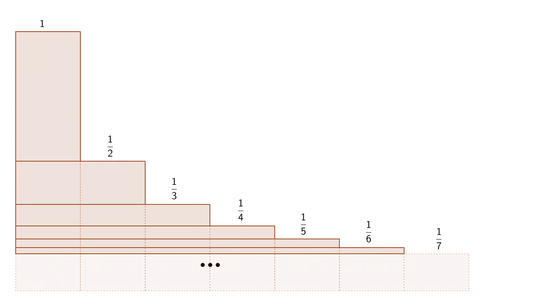
I think that an easily comprehensible explanation, the intuitive one, will kind of come after contemplation on the rate of decreasing of members of the series.

The best I could find on the topic is the way Augustin-Louis Cauchy developed his condensation test

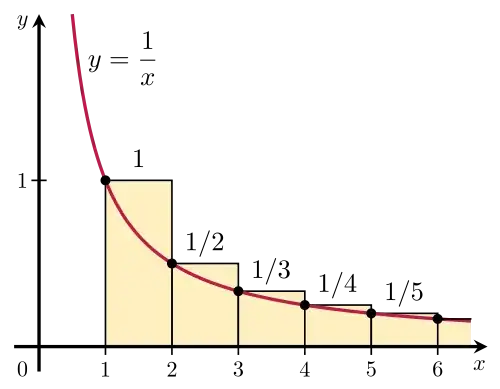
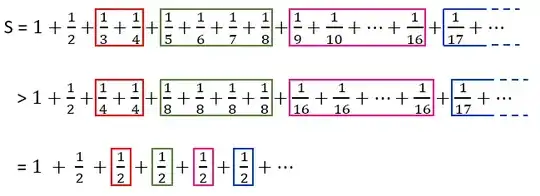
Cauchy for sure was contemplating on the members decrease rate and was trying to model his test based on Oresme's beautiful idea. The main question is - how slow should members of the series decrease, so that you can guarantee that a fixed amount of subsequent members can reach the magnitude of the first member? For harmonic series the sum of $2^{n-1}$ subsequent members will always reach $\frac{1}{2}$. What about other series?

I was thinking about this main question before I discovered Cauchy condensation test. The feeling is - when the series decrease rapidly, with high acceleration, you go to infinity faster than the sum of subsequent members can reach the first member. In other words, the subsequent members cannot compensate, all together, on their rapid fall.

How rapidly? What's the criteria to say - starting with this rate of decreasing, the series will converge? I came up with an intuitive criteria, and described it at Can second derivative indicate convergence of infinite series?

My criteria was

If you have a series $\sum_{n=1}^{+\infty}\frac{1}{f(n)}$ where $f(n)$ is monotonically-increasing function, then if $f(n)$ increases faster than linearly then the series converges; if $f(n)$ grows linearly or slower, the series will diverge. In other words, if $f''(n)>0$ the series converges; otherwise, it diverges.

Note that $f(n)$ is the denominator of the series.

I was then shown that for $f(n) = n\log n$ my criteria doesn't work. Second derivative $f''(n\log n)=\frac{1}{n} > 0$ but the series diverges! So even when $f(n)$ grows slightly faster than linear, the series can still diverge. This is the simplest example of Bertrand series that can converge or diverge arbitrarily slowly.

But I am sure that my criteria is very close to truth.

So the answer to the question

How rapidly?

must be very close to

$f′′(n)>\frac{const}{n}$

So, I can amend my criteria to be

If $f′′(n)>\frac{const}{n}$ the series converges; otherwise, it diverges.

I cannot prove it, but it is clear that starting with some acceleration of growing of $f(n)$, the series will always converge, because the members of $\frac{1}{f(n)}$ will start decreasing too fast.