17

Consider the identity $(b-a)(b+a) = ab - 1$, where $a, b$ are nonnegative integers.

We can also express this identity as $a^2 + ab - b^2 = 1$.

This identity is clearly true when $a = F_{2i-1}$ and $b = F_{2i}$, where $F_i$ is the $i^{th}$ term of the Fibonacci sequence. This is equivalent to one case of Cassini's identity, $(F_{2i-1})(F_{2i+1}) = F_{2i}^2 + 1$, and is easily proven by induction or several other simple elementary means.

My question is this: Is there a simple elementary proof that these Fibonacci numbers are the only solutions of this identity?

By simple elementary proof, ideally I mean a proof using methods and steps that a mathematically gifted high school student could follow and understand. Alternatively, I could define it as a proof using methods that would have been known to mathematicians in Cassini's time, in the late 17th century. In other words, I am looking for a proof that does not rely on more advanced methods such as quadratic number fields or generalized solutions of Pell equations.

BR Pahari
  • 2,694
Geoffrey Caveney
  • 559
  • 1
    For the benefit of readers who are interested in the more advanced solution, the first step is to observe that $a^2 + ab - b^2$ is the norm form $N(a + b \phi)$ where $\phi = \frac{1 + \sqrt{5}}{2}$ is the golden ratio and $N$ refers to the norm in the ring of algebraic integers $\mathcal{O}_{\mathbb{Q}(\sqrt{5})} = \mathbb{Z}[\phi]$. So we can find all solutions by computing generators for the unit group, since units are precisely the elements of norm $\pm 1$. – Qiaochu Yuan Dec 03 '17 at 19:19
  • Very simple with Conway's Topograph diagram, see new book http://bookstore.ams.org/mbk-105/ – Will Jagy Dec 03 '17 at 19:26
  • 1
    Ok yes rtybase after careful study of the answer you provide there, I accept that it also answers my question. The key point, for me, is your argument in the "descent" step that n>q>0 or n=q=1, because if q>=n, then q^2+nq-n^2 >= n^2+n^2-n^2=n^2>=1. But q^2+nq-n^2=1 or -1, so q>=n can only be true if n=q=1. This is the key step to make the proof complete. Now we can effectively use the descent method to show that the sequence must eventually reach n=q=1, so all of the solutions must indeed be Fibonacci numbers. Thank you! – Geoffrey Caveney Dec 04 '17 at 00:43

3 Answers3

8

Here's one approach:

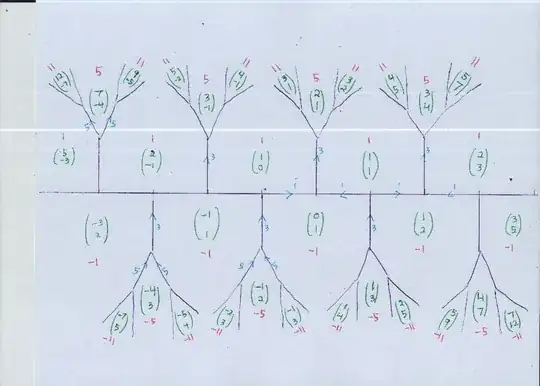
Step 1a: Show that if $a$ and $b$ satisfy this, and $0 < a < b$, then $a' = (b-a)$ and $b' = a$ also satisfy it and have $a' \le b' < b$, so that the max absolute value of the two items in the pair decreases

What the heck...let's check that: we want to show that $(b' - a') (b' + a') - (a'b' -1) $ is zero. So compute \begin{align} (b' - a') (b' + a') - (a'b' -1) &=(a - (b-a)) (a + (b-a)) - (a(b-a) -1)\\ &=(2a - b)) (b)) - (a(b-a) -1)\\ &=2ab - b^2 - ab + a^2 +1 \\ &=ab - b^2 + a^2 +1 \end{align} which is $0$ because $a$ and $b$ satisfy the relation, which expanded out says that $b^2 - a^2 - ab + 1 = 0$.

Case 1b: if $b < a < 0$, then $b' = b-a$ and $a' = b$ do as well, and $b' < a' < 0$, and $|b'| = |a| < |b|$. Proof: exactly the same as before. Once again, the max absolute value of the two items in the pair decreases.

Case 1c: $b$ and $a$ have opposite signs. If $b$ is positive, then $a$ is negative, and $|a| > |b|$. If $b$ is negative, then $a$ is positive, so $b-a$ is negative, so $b+a$ is positive, and once again $|a| > |b|$. Again, by an argument like the one above, the pair $(a, b)$ can be adjusted to a pair $(b, a-b)$ where the larger number (in absolute value) is smaller in the new pair than in the old one, i.e., the max absolute value of the two items in the pair decreases.

Other cases: you still have to deal with other similar cases in ways rather like this, and I don't have the stomach to go through it all.

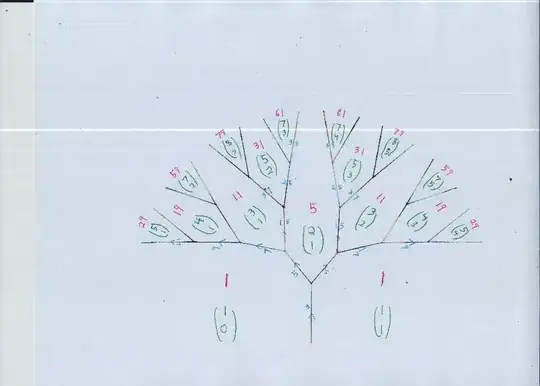
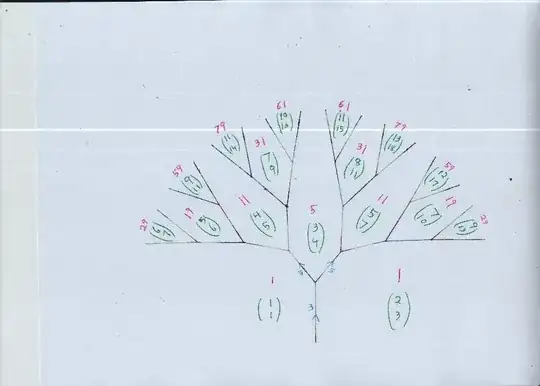
Step 2: Conclude that for any such pair, we can reduce the pair to a smaller (in the sense of max-absolute-value) pair of numbers, until until $a = b$ (which fails unless $a = b = \pm 1$).

Step 3: Conclude that our pair is part of the sequence that arises from $(1, 1) \to (1, 2) \to (2, 3) \to (3, 5) \to ...$, i.e., the F-sequence.

[This does only handle the case where $0 < a < b$; the $a=b$ case is trivial (indeed, Step 2 addresses it); the $a > b$ case can almost certainly be handled by essentially the same method. The case where $a$ or $b$ is zero should not be difficult for a bright high-school student.]

John Hughes
  • 93,729
  • A small comment is likely necessary for the $(1, 0)$ case, but otherwise I like this answer! – B. Mehta Dec 03 '17 at 19:14
  • 3
    This is classical problem with Vieta jumping solution. – nonuser Dec 03 '17 at 19:16
  • Thanks, @B.Mehta; I'd forgotten to mention those cases. John Watson: I guess I need to read about Vieta jumping solutions -- is that the general case of what I just wrote out? – John Hughes Dec 03 '17 at 19:17
  • 1
    https://en.wikipedia.org/wiki/Vieta_jumping – nonuser Dec 03 '17 at 19:19
  • See my comment on the other answer below. The difficulty is that the identity can also be valid for negative integers as well, so hypothetically it is possible that such a sequence could go from large positive numbers to negative numbers in one step, and continue with smaller negative numbers (larger absolute value) from there to negative infinity. A proof must rule out this possibility. – Geoffrey Caveney Dec 03 '17 at 19:21
  • The algorithm I gave cannot jump from positive to negative numbers, because I only consider pairs $(x, y)$ where $x < y$, and replace this with the pair $(y-x, x)$, in which both terms remain positive. – John Hughes Dec 03 '17 at 19:32
  • John there is a fairly painless approach with Conway's topograph. There is also a recent, elementary book, lots of figures, http://bookstore.ams.org/mbk-105/ . A strength of the topograph is finding all solutions when the target number has small absolute value. – Will Jagy Dec 03 '17 at 19:35
  • John, this is true, but then in the next step, can you be certain that y-x < x ? Eventually you will reach a step where the first number may be greater than the second number, equivalent to the a > b case that you mention at the end. And this leads straight to negative integers, which do not reduce to a smallest pair of numbers. – Geoffrey Caveney Dec 03 '17 at 19:41
  • I've slightly adjusted to handle that. Will's approach is more general (and actually does all the cases!), but therefore necessarily more complicated. – John Hughes Dec 03 '17 at 20:04
  • As I asked about Will's answer, I'm curious about how your method would handle the case of (b-a)(b+a) = ab - 11. Here you have solutions in the sequence 1,4,5,9,14,23,37,60,..., but you also have solutions in the sequence 2,5,7,12,19,31,50,.... How would your approach include both cases but rule out any others? – Geoffrey Caveney Dec 03 '17 at 20:12
  • John, I also want to say thank you very much for all of the methods and ideas you have contributed. Just because I keep asking more and more detailed questions about more and more particular cases, does not mean I don't appreciate the value of the material that you have already contributed! – Geoffrey Caveney Dec 03 '17 at 20:29
  • As for $ab - 11$ --- I have no idea. I'm not even close to being a number-theory person; this just seemed like something I could address with methods I knew. (I"m sorta like your bright high-school senior in that sense). I suspect that the "simplifying" tricks I'm using would be more complex, and in some cases might lead to "replace (a, b) with either (a-b, 2b-3a) OR with (b-2a, 3a - 2b +1), depending on ..." or something like that, and it'd all get much messier. The particular equation you gave is rather nice, because the number 1 is, among integers, pretty small. :) – John Hughes Dec 03 '17 at 20:57
  • @GeoffreyCaveney I pasted in a tree that shows solutions for $a^2 + ab - b^2 =11.$ The Climbing Lemma says there are no more such solutions in the given tree. Periodicity says all other solutions come from the initial pair by simple arithmetic; Cayley-Hamiton then says that these can be separated into linear recurrences in the separate variables, which is how we get things like the Fibonacci numbers in the first place. Oh, I don't think anyone else calls them trees. My style of drawing... – Will Jagy Dec 04 '17 at 00:56
  • You got some signs mixed up. Is $a^2+ab-b^2=+1$ or $-1$? By the way, I like to view these pairs as perplex numbers $$a+b\hat\varphi=a+b\frac{1+j\sqrt5}{2}=\Big(a+\frac12b\Big)+j\Big(\frac{\sqrt5}{2}b\Big)=x+yj$$ so that $$(x+yj)(x-yj)=x^2-y^2=a^2+ab-b^2=\pm1$$ represents the unit hyperbolas, and your map $(a,b)\mapsto(b-a,a)$ is multiplication by $\hat\varphi^{-1}$. – mr_e_man Feb 05 '20 at 01:46
2

Open this up to solving $a^2+ab-b^2=\pm1$ in positive integers. Unless $a$ and $b$ are very small, then $a<b$. Let $c=b-a$. Then $$c^2+ca-a^2=(b-a)^2+(b-a)a-a^2=-a^2-ab+b^2=\mp1.$$ So if $c$ and $a$ are consecutive Fibonacci's then so are $a$ and $b$.

To complete this, one needs to analyse the solutions for small $a$ and $b$ in order to start off the induction.

Angina Seng
  • 158,341
  • Thank you for the replies and ideas, but the difficulty with this approach of proof by "descent" to smaller terms is that the identity can also be valid for negative integers as well, which can also obey Fibonacci-like sequence relations. So one cannot say that an arbitrary a, b will necessarily reduce to small positive numbers like a=b=1. Hypothetically it could be possible that such a sequence could go from large positive numbers to negative numbers in one step, and continue with smaller negative numbers (larger absolute value) from there to negative infinity. A proof must rule this out. – Geoffrey Caveney Dec 03 '17 at 19:18
1

It turns out I have a diagram of Conway's topograph pdf for this. The very simple statement is that "the river is periodic." This means that, if we can find all solutions within one period, we have them all.

Recent book by Allen Hatcher pdf

ALSO: Recent book at a fairly elementary level: Weissman

Broken down further, it means that any solution to $a^2 + ab - b^2 = 1$ leads to another, $$ (a,b) \mapsto (a+b, a + 2b) $$ As you can see from the (vertical) vectors when the form value is $1,$ this makes $a,b$ consecutive Fibonacci, by induction.

As you can see, I draw in little $(x,y)$ "coordinate" pairs as column vectors. This is crucial for my approach; the other two books do not really push this aspect, but it is done well in Stillwell, Elements of Number Theory.

enter image description here

I have drawn a portion of the river, with colors as in the tree diagrams, and showing the relative positions of the values $11.$ I have worked out how to force the given mapping $ (a,b) \mapsto (a+b, a + 2b) $ as we move to the right, or $ (a,b) \mapsto (2a-b, -a + b) $ as we move to the left.

enter image description here

There was a question in comment about $a^2 + ab - b^2 = 11.$ It is enough to draw a single "tree" of positive values climbing away from the river. We see $11$ as $(a,b)$ pairs $(3,1)$ and $(3,2).$ All other solutions with positive $(a,b)$ occur in other trees along the river. They can be found with $ (a,b) \mapsto (a+b, a + 2b) .$ In the next tree to the right, we get $(4,5)$ and $(5,7).$ A second tree to the right, we get $(9,14)$ and $(12,19).$ Also, Cayley-Hamilton says that we get two orbits under a pair of linear degree two recurrences, $$ a_{n+2} = 3 a_{n+1} - a_n, $$ $$ b_{n+2} = 3 b_{n+1} - b_n. $$ I wrote out a simple proof without using Cayley-Hamilton at How does one solve this recurrence relation?

enter image description here

Alright, I did one tree over, I mostly left off the blue edge labels, which match the previous tree.

enter image description here

Other answers/questions I did with the topograph:

http://math.stackexchange.com/questions/342284/generate-solutions-of-quadratic-diophantine-equation/346821#346821

http://math.stackexchange.com/questions/81917/another-quadratic-diophantine-equation-how-do-i-proceed/144794#144794

http://math.stackexchange.com/questions/228356/how-to-find-solutions-of-x2-3y2-2/228405#228405

http://math.stackexchange.com/questions/342284/generate-solutions-of-quadratic-diophantine-equation/345128#345128

http://math.stackexchange.com/questions/487051/why-cant-the-alpertron-solve-this-pell-like-equation/487063#487063

http://math.stackexchange.com/questions/512621/finding-all-solutions-of-the-pell-type-equation-x2-5y2-4/512649#512649

http://math.stackexchange.com/questions/680972/if-m-n-in-mathbb-z-2-satisfies-3m2m-4n2n-then-m-n-is-a-perfect-square/686351#686351

http://math.stackexchange.com/questions/739752/how-to-solve-binary-form-ax2bxycy2-m-for-integer-and-rational-x-y/739765#739765

http://math.stackexchange.com/questions/742181/find-all-integer-solutions-for-the-equation-5x2-y2-4/756972#756972

http://math.stackexchange.com/questions/822503/positive-integer-n-such-that-2n1-3n1-are-both-perfect-squares/822517#822517

http://math.stackexchange.com/questions/1078450/maps-of-primitive-vectors-and-conways-river-has-anyone-built-this-in-sage/1078979#1078979

http://math.stackexchange.com/questions/1091310/infinitely-many-systems-of-23-consecutive-integers/1093382#1093382

http://math.stackexchange.com/questions/1132187/solve-the-following-equation-for-x-and-y/1132347#1132347 <1,-1,-1>

http://math.stackexchange.com/questions/1132799/finding-integers-of-the-form-3x2-xy-5y2-where-x-and-y-are-integers

http://math.stackexchange.com/questions/1221178/small-integral-representation-as-x2-2y2-in-pells-equation/1221280#1221280

http://math.stackexchange.com/questions/1404023/solving-the-equation-x2-7y2-3-over-integers/1404126#1404126

http://math.stackexchange.com/questions/1599211/solutions-to-diophantine-equations/1600010#1600010

http://math.stackexchange.com/questions/1667323/how-to-prove-that-the-roots-of-this-equation-are-integers/1667380#1667380

http://math.stackexchange.com/questions/1719280/does-the-pell-like-equation-x2-dy2-k-have-a-simple-recursion-like-x2-dy2

http://math.stackexchange.com/questions/1737385/if-d1-is-a-squarefree-integer-show-that-x2-dy2-c-gives-some-bounds-i/1737824#1737824

http://math.stackexchange.com/questions/1772594/find-all-natural-numbers-n-such-that-21n2-20-is-a-perfect-square/1773319#1773319

Will Jagy
  • 139,541
  • Thank you for the illustration, but I just wonder, doesn't the math behind Conway's topograph require essentially the same advanced abstract algebra methods that Qiaochu Yuan mentioned in his answer above? I don't believe that an automorphism group is a concept that a high school student or a 17th century mathematician could comprehend. – Geoffrey Caveney Dec 03 '17 at 19:47
  • Also, are you sure that this method proves the impossibility of other solutions in other sequences? For example, let's say I claimed all solutions of (b-a)(b+a) = ab - 11 were in the sequence 1,4,5,9,14,23,37,60,.... As in your method, induction shows that each solution in the sequence leads to another. But in fact in this case there is a different sequence with solutions: 2,5,7,12,19,31,50,.... Can your method identify both sequences? How? – Geoffrey Caveney Dec 03 '17 at 20:05
  • @GeoffreyCaveney yes, I'm sure. When you switch to a prime, in your case $11,$ you expect two orbits. Forget the word automorphism. It is just an explicit integer mapping that takes locations in the topograph to others with the same quadratic form. Recommend you learn the method, here is Conway's original http://www.maths.ed.ac.uk/~aar/papers/conwaysens.pdf – Will Jagy Dec 03 '17 at 20:13
  • @GeoffreyCaveney added links to some topograph answers. Recommend you learn how to draw them. Also, given your concerns, suggest you look at http://math.stackexchange.com/questions/739752/how-to-solve-binary-form-ax2bxycy2-m-for-integer-and-rational-x-y/739765#739765 where, because $55$ is composite, there are several orbits; these are readily found in the "trees" I draw. – Will Jagy Dec 03 '17 at 20:19
  • The Conway monograph is very interesting, thank you Will. I will look into it and your examples further. – Geoffrey Caveney Dec 03 '17 at 20:22
  • @GeoffreyCaveney I added that the business of drawing in (x,y) column vector "coordinates" is dealt with best in Stillwell's book, Elements of Number Theory. You will see, I had to be very careful about the dimensions and spacing of my diagrams, to fit in all the types of numerical labels. However, combining periodicity of the river and The Climbing Lemma, finding all solutions of "form equals target number" is just very careful drawing and labelling of diagrams. – Will Jagy Dec 03 '17 at 20:32
  • 1
    Just to clarify for other readers, Conway's concepts like "the river is periodic" that Will mentions do make sense, but only if you carefully work through the First Lecture of Conway's book The Sensual (Quadratic) Form, "Can You See The Values of 3x^2 + 6xy - 5y^2?" The terms "topograph", "river", "lake", "tree", "well", etc., have specific definitions in the context of Conway's treatment of quadratic forms, lattices, matrices, vectors, bases, norms, etc. One must work through all of this material, for terms like "the river" to make mathematical sense. – Geoffrey Caveney Dec 03 '17 at 20:45