I am looking for integer solutions to the equation $$x^2 = 5y^2 + 14y + 1$$ I know that Pell's Equation is of the form $x^2 - ny^2=1$ and that there exist algorithms to solve this equation. I was wondering if it is along the right track to try to transform this into something that looks like pell's equation? If so, what kind of substitution would I need to make to make it work?
-
I put in a bit more, on some degree two linear recurrences in one variable each. Based on Cayley-Hamilton. – Will Jagy Jan 04 '16 at 23:26
2 Answers
Multiply by $5,$ you get $$ (5y+7)^2 - 5 x^2 = 44. $$
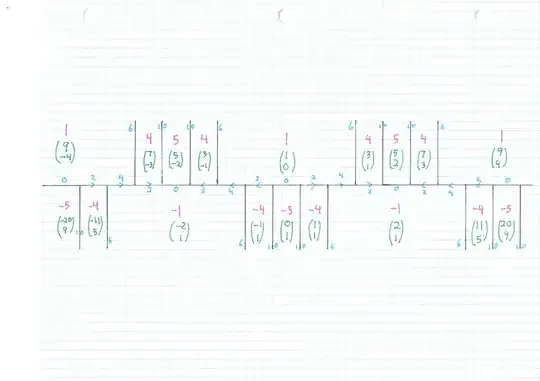
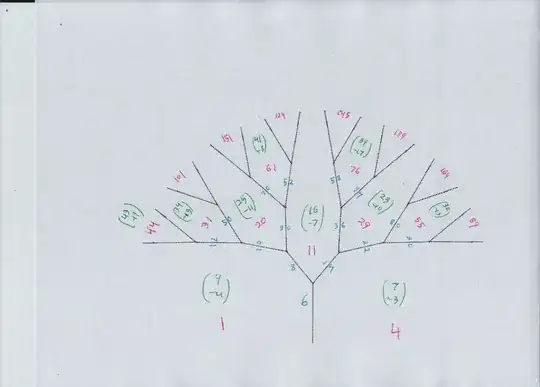
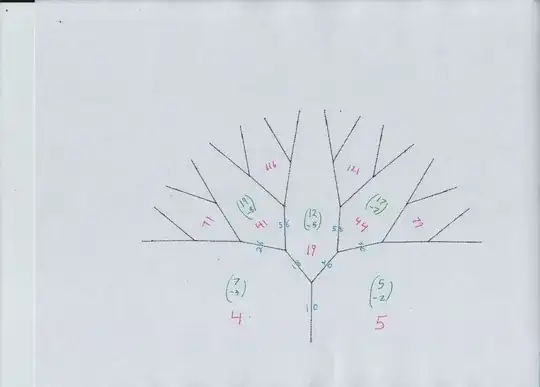
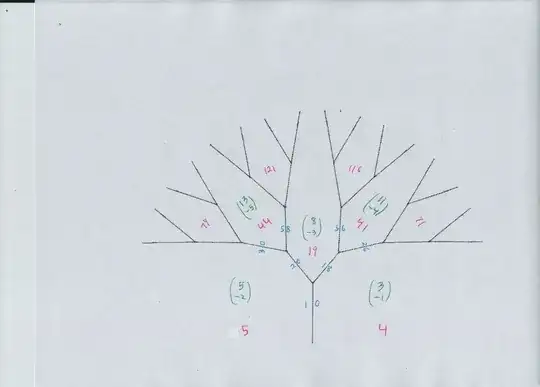
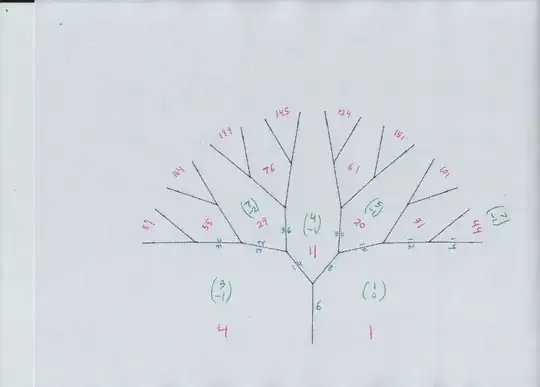
A way to be sure that all solutions have been found in a Pell type problem is Conway's topograph diagram. The way I draw it now is one main diagram of the "river," then one or more trees growing off the river. The conclusion is that all solutions to $$ u^2 - 5 v^2 = 44 $$ come from tree locations (green vectors) $$(32,-14), (43,-19),(17,-7),(13,-5),(16,-4),(8,-2). $$ Note that $(32, -14)$ is simply double $(16,-7),$ because the latter is a representation of $11.$ Same with $(8,-2).$
For your problem you need to negate any possible pair, at least negate the first coordinate $u,$ because you have $u = 5y+7.$ For example, $u=7$ is a useful solution for you, but $u=-7$ is not. Together, a dozen "seed" pairs $$ ( -43, 19), ( -32, 14), ( -17, 7), ( -13, 5), ( -8, 2), ( -7, 1), ( 7, -1), ( 8, -2), ( 13, -5), ( 17, -7), ( 32, -14), ( 43, -19). $$
together with the rules for transforming solutions (below) give everything needed. What becomes clear from looking at the river diagram is that. Or, you can stick with the half dozen original seeds, in $u$ order $$( 43, -19), ( 32, -14), ( 17, -7), ( 13, -5), ( 8, -2), ( 7, -1), $$ find all transformed pairs, and every time you get a new $(u,v)$ also consider $(-u,v).$ That is what I would do...
Given solution $(u,v)$ to $u^2 - 5 v^2 = 44,$ we get new solutions going to the right or to the left in the Conway diagram by transforming to either $$ (u,v) \mapsto (9 u + 20 v, 4 u + 9 v ) $$ or $$ (u,v) \mapsto (9 u - 20 v, -4 u + 9 v ) $$ There are therefore infinitely many solutions, but these are all.
For the six positive $u$ I displayed, $$ 5y+7 = 7, y=0, x^2 = 1, $$ $$ 5y+7 = -8, y=-3, x^2 = 4, $$ $$ 5y+7 = -13, y=-4, x^2 = 25, $$ $$ 5y+7 = 17, y=2, x^2 = 49, $$ $$ 5y+7 = 32, y=5, x^2 = 196, $$ $$ 5y+7 = -43, y=-10, x^2 = 361, $$
NOTE: by the Cayley-Hamilton Theorem, the (keep the positive values) of $u$ split into six sequences that obey $$ \color{red}{ u_{n+2} = 18 u_{n+1} - u_n.} $$
Here are the six orbits:
( 43, -19), ( 7, 1), ( 83, 37), ( 1487, 665), ( 26683, 11933),
( 32, -14), ( 8, 2), ( 112, 50), ( 2008, 898), ( 36032, 16114),
( 17, -7), ( 13, 5), ( 217, 97), ( 3893, 1741), ( 69857, 31241),
( 13, -5), ( 17, 7), ( 293, 131), ( 5257, 2351), ( 94333, 42187),
( 8, -2), ( 32, 14), ( 568, 254), ( 10192, 4558), ( 182888, 81790),
( 7, -1), ( 43, 19), ( 767, 343), ( 13763, 6155), ( 246967, 110447),
These give six $u$ orbits under $ u_{n+2} = 18 u_{n+1} - u_n$ $$ 7, 83, 1487, 26683,... $$ $$ 8, 112, 2008, 36032,... $$ $$ 13, 217, 3893, 69857,... $$ $$ 17, 293, 5257, 94333,... $$ $$ 32, 568, 10192, 182888,... $$ $$ 43, 767, 13763, 246967,... $$ For every $u$ value in any of the six, we can solve either $5y+7 = u$ or $5y+7 = -u$ in integers.
If you prefer, you also get six $v$ orbits that obey $$ \color{red}{ v_{n+2} = 18 v_{n+1} - v_n.} $$
And these are the diagrams, river and trees i called A,B,C,D...
Another quadratic Diophantine equation: How do I proceed?
How to find solutions of $x^2-3y^2=-2$?
Generate solutions of Quadratic Diophantine Equation
Finding all solutions of the Pell-type equation $x^2-5y^2 = -4$
how to solve binary form $ax^2+bxy+cy^2=m$, for integer and rational $ (x,y)$
Find all integer solutions for the equation $|5x^2 - y^2| = 4$
Maps of primitive vectors and Conway's river, has anyone built this in SAGE?
Infinitely many systems of $23$ consecutive integers
Small integral representation as $x^2-2y^2$ in Pell's equation
Solving the equation $ x^2-7y^2=-3 $ over integers
Solutions to Diophantine Equations
http://www.maa.org/press/maa-reviews/the-sensual-quadratic-form (Conway)
http://www.springer.com/us/book/9780387955872 (Stillwell)
-
+1! Will, do you have a reference for Conway's topograph diagram method for tracking solutions to Pell's equation? – Jose Arnaldo Bebita Dris Jan 04 '16 at 19:54
-
@ArnieDris edited in some links, including the books of Conway (just the first chapter, really) and Stillwell. I have tinkered with the drawings to emphasize the automorphism group of the form, that is the $(9u+20u, 4u+9v)$ stuff, which does appear explicitly in the river diagram. – Will Jagy Jan 04 '16 at 20:19
For these equations we use the standard approach. For a private quadratic form: $$Y^2=aX^2+bX+1$$
Using solutions of Pell's equation: $$p^2-as^2=1$$
Solutions can be expressed through them is quite simple.
$$Y=p^2+bps+as^2$$
$$X=2ps+bs^2$$
$p,s$ - these numbers can have any sign.
Finding solutions of equations Pell - standard procedure.
- 4,301
-
-
@MosBlack We should consider all the signs. $p^2-as^2=-1$ As well as different sign $p,s$. – individ Jan 04 '16 at 07:40
-
If I get the fundamental solution to that pell's equation, and use the recurrence formula to generate all other solutions. Will this give me all possible solutions? – ultrainstinct Jan 04 '16 at 07:51
-
@Panphobia The way to do it. Some formulas are there to obtain the following solutions for previous. http://www.artofproblemsolving.com/community/c3046h1098490_a_variation_of_the_same_identity http://www.artofproblemsolving.com/community/c3046h1090811_the_general_pell_equation – individ Jan 04 '16 at 07:59