2

Let there be an equation $a^2 + 4ab + b^2 - 121 = 0$ where I want to prove that a,b are integers. Then I want to find whether there are integer values of $b$ for which $a$ is also an integer. Let us consider the case for $a$ $\rightarrow$ $a = \dfrac{-4b \pm \sqrt{16b^2 - 4(b^2-121)}}{2} = -2b \pm \sqrt{3b^2 +121}$ Thereby the problem reduces to showing that $3b^2 +121$ is a perfect square for certain integer values of $b$. This is what I cannot do.

Note: I know I can give examples and all for $3b^2 + 121$ to be a perfect square, but I'm looking for something with a little more substance. Thanks for the help.

Airdish
  • 2,471
  • 1
    I'm a little unclear about the original problem. The way you have stated it, I can have non-integer solutions as well. – Shailesh Feb 22 '16 at 16:42
  • Not all solutions of this equation are integral. – Wojowu Feb 22 '16 at 16:42
  • @Wojowu Hmm. Yeah, I had my misgivings. Is there any way to show that there is a pair of $a, b$ for which the equation holds? I know that a,b = 5, 4. But I only found this by plugging in values. And so I have no way of showing that there is an integral solution. – Airdish Feb 22 '16 at 16:45
  • You have a way of showing existence of integer solutions - providing an example is a perfectly valid method! – Wojowu Feb 22 '16 at 16:46
  • @Wojowu But I'd like a more concrete way... for my own curiosity and personal satisfaction I guess – Airdish Feb 22 '16 at 16:47
  • Precision matters. What you want to prove is that a and b can both be integers. Not that they must be integers. Obviously there are non-integer solution. um.. a=0 and b= 11 and a = 0 and b=11 are solutions too. – fleablood Feb 22 '16 at 17:38
  • 1
    $12b^{2} + 4\times 11^{2}$ is a square if and only if $(3b^{2} + 11^{2}) = s^{2} \iff 3|(s-11)(s +11)$ and the smallest positive $s$ for which this happens is $s = 14$, which yields $b^{2} = 5^{2}$. – Daniel Akech Thiong Feb 22 '16 at 17:51
  • 1
    To all; there are infinitely many solutions with both $a,b$ integers. Doubtless the original question in some book or contest asked to find at least some of these. Answer posted below. – Will Jagy Feb 22 '16 at 18:00

2 Answers2

4

EDIT: There are infinitely many integer solutions. They can all be found. In particular, if you have one solution $(a,b)$ you get a new solution with $$ (a,b) \mapsto (-b, a + 4 b). $$ Going in the reverse direction, $$ (a,b) \mapsto ( 4a + b, -a). $$ For solutions to $a^2 + 4ab + b^2 = 121,$ we will almost always need $ab < 0.$

Um. The generator for the (oriented) integer automorphism group of the quadratic form $a^2 + 4ab + b^2$ is $$ A = \left( \begin{array}{rr} 0 & -1 \\ 1 & 4 \end{array} \right), $$ with inverse $$ A^{-1} = \left( \begin{array}{rr} 4 & 1 \\ -1 & 0 \end{array} \right). $$ The degree two linear recurrences that follow come from applying Cayley-Hamilton to $A,$ in that $A^2 - 4A + I = 0.$

In the original variables, we can collect all solutions into Fibonacci type sequences, as in $a_{n+2} = 4 a_{n+1} - a_n$ and $b_{n+2} = 4 b_{n+1} - b_n$ $$ \begin{array}{rrrrrrrrrrr} -4736 & -1269 & -340 & -91 & -24 & -5 & 4 & 21 & 80 & 299 & 1116 \\ 1269 & 340 & 91 & 24 & 5 & -4 & -21 & -80 & -299 & -1116 & -4165 \end{array} $$ We can do the same thing for the solutions where both $(a,b)$ are divisible by $11.$ Oh, not only can we switch the variables, we can always negate both. So $(-5,-4)$ gives us $(5,4)$ and $(4,5).$ $$ \begin{array}{rrrrrrrrrr} -616 & -165 & -44 & -11 & 0 & 11 & 44 & 165 & 616 & 2299 \\ 2299 & 616 & 165 & 44 & 11 & 0 & -11 & -44 & -165 & -616 \end{array} $$

ORIGINAL: take the invertible change of variables $$ a = u - 2 v, \;\; \; b = v,$$ so that $a + 2 b = u.$ You have $$ u^2 - 3 v^2 = 121. $$ There are the imprimitive solutions where $u,v$ are solutions of $u^2 - 3 v^2 = 1$ then multiply both by $11.$ There are infinitely many of these, this is called the Pell equation.

There are also infinitely many imprimitive solutions to $u^2 - 3 v^2 = 121.$ This begins with $1 - 3 \cdot 4 = -11,$ and Brahmagupta's formula leads to $13^2 - 3 \cdot 4^2 = 11^2.$

In both cases, given values $(u,v),$ changing to $(2u+3v, u + 2 v)$ gives the same value of $u^2 - 3 v^2.$ You should check that, important.

A full accounting of all $(u,v)$ pairs is given by combining the $(2u+3v, u + 2 v)$ formula with the Conway topograph.

Here are some answers with the topograph , then two books that talk about it:

Another quadratic Diophantine equation: How do I proceed?

How to find solutions of $x^2-3y^2=-2$?

Generate solutions of Quadratic Diophantine Equation

Finding all solutions of the Pell-type equation $x^2-5y^2 = -4$

how to solve binary form $ax^2+bxy+cy^2=m$, for integer and rational $ (x,y)$

Find all integer solutions for the equation $|5x^2 - y^2| = 4$

Maps of primitive vectors and Conway's river, has anyone built this in SAGE?

Infinitely many systems of $23$ consecutive integers

Finding integers of the form $3x^2 + xy - 5y^2$ where $x$ and $y$ are integers, using diagram via arithmetic progression

Small integral representation as $x^2-2y^2$ in Pell's equation

Solving the equation $ x^2-7y^2=-3 $ over integers

Solutions to Diophantine Equations

http://www.maa.org/press/maa-reviews/the-sensual-quadratic-form (Conway)

http://www.springer.com/us/book/9780387955872 (Stillwell)

I'm afraid I was not able to fit this entire diagram onto one page. However, combine this with How to find solutions of $x^2-3y^2=-2$? and you get all integer expressions for $u^2 - 3 v^2 = 121,$ which then lead to all $a^2 + 4ab + b^2 = 121.$

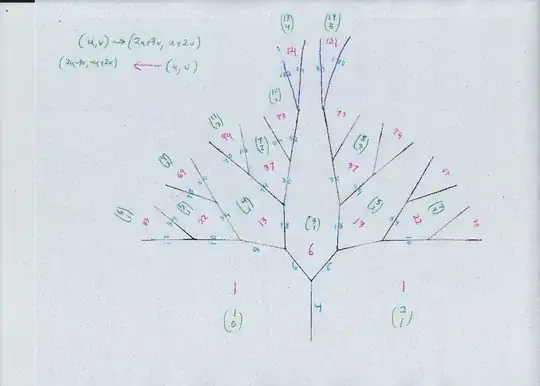
enter image description here

All solutions $(u,v)$ come from the transformation $(2u+3v, u + 2 v),$ its inverse $(2u-3v, -u + 2 v),$ and the three triples $$ (11,0), (13,4),(14,5) $$ Some care is need for the original $(a,b)$ problem because the change of variables does not quite keep positivity. Indeed, instead of the $\pm$ symmetries, the original variables have $(a,b)$ going to $(b,a).$

Community
  • 1
Will Jagy
  • 139,541
  • I'm gonna be honest with you. You lost me after $u^2 - 3v^2 = 121$. As you've probably guessed, I have no experience in number theory. I am just a beginner in high school and I'm trying to learn the works of the trade. So if you could give some more layman explanations, that would be great. – Airdish Feb 22 '16 at 18:31
  • Furthermore, is there a way to find the solutions to this equation using no number theory at all? (Or at the most, very basic number theory?) – Airdish Feb 22 '16 at 18:35
  • I've edited my question to include a more basic, straightforward approach which I believe could work. Could you follow up on it, if you have the time? – Airdish Feb 22 '16 at 18:44
  • 1
    @S.Mo who gave you this question and why did they do that? What did they hope you would accomplish? – Will Jagy Feb 22 '16 at 18:59
0

From $a^2+b^2+4ab-121=0$ we get $(a+b)^2+2ab=121$
Or $2=\frac{11+a+b}{a} \frac{11-a-b}{b}$
Now case 1: when the factors on right hand side are integers and coprime. Since 2 has only 2 factors, one of these has to be 1 and the other 2
Taking $\frac{11+a+b}{a}=2$ and $\frac{11-a-b}{b}=1$ we get $a=11 , b=0$
Similarly $\frac{11+a+b}{a}=1$ and $\frac{11-a-b}{b}=2$ gives $a=44$ and $b=-11$



I can't do the case where those factors are not integers or coprime right now (note that's the case of $a=5,b=4$)

Aniket Bhattacharyea
  • 991