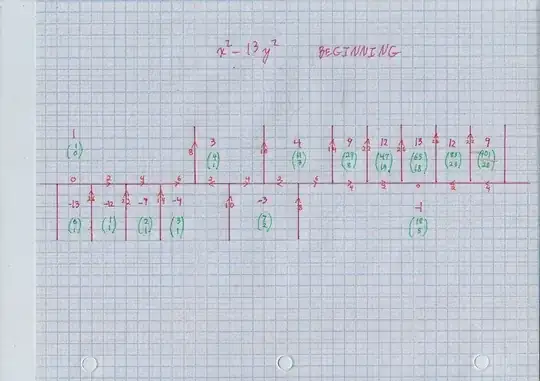
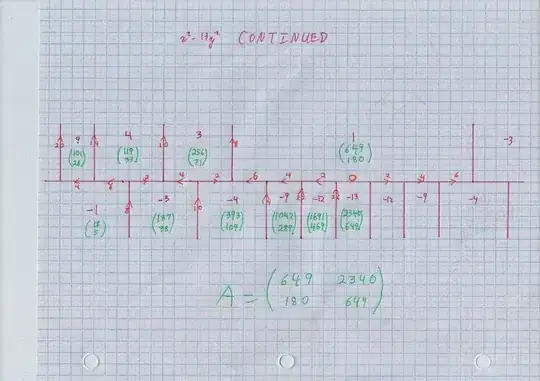
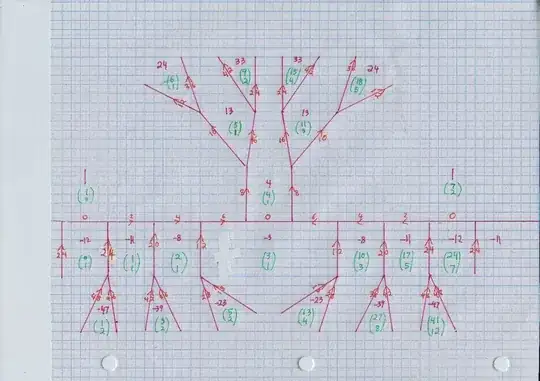
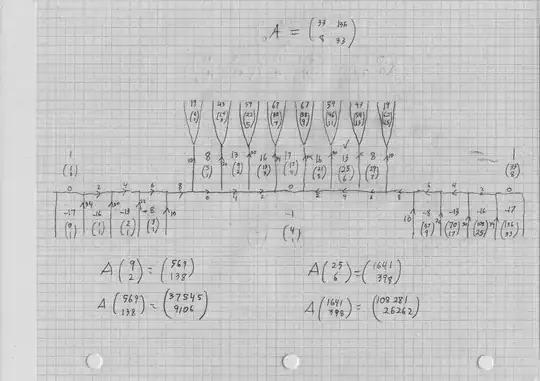
EDIT, January 2017: the property proved in this answer is in a book by Franz Lemmermeyer called Binary Quadratic Forms, Theorem 1.36, numbered page 37, pdf page 43 in my viewer. The part with $AC < 0, B > |A+C|$ is formula (1.34) there.
This is a proof of something I mentioned to awllower in comment, somewhere. In my diagrams of Conway's topograph, I draw the "river" as a straight line, and edges leaving it as perpendicular to the river. On page 20 in Conway's book, we read
In other words, if you stray from the river, the values go up (in
absolute value).
So I started calling these orthogonal edges "straying edges." Now, most of the time, you get several straying edges in a row on the same side of the river. But then, you find a place where one straying edge is on one side of the river, the very next straying edge is on the other side. I decided to call this "crossing the river." Because I am clever that way.
EDIT: Martin Weissman of U. C. Santa Cruz is writing a book on number theory that will include and expand upon the Conway topograph. He likes to call these special locations riverbends. His image, and the illustrations in Conway's book, have the river in something of a sinuous shape, for a while arcing around a positive value, then bending the other way and arcing around a negative value, and so on. As I drew my diagrams on graph paper and made all edges straight and the river a straight line, so this attractive image does not come across. The blog about progress on the book is HERE
Let me emphasize that each edge with a little orange arrow and number refers to an indefinite quadratic form $\langle a,b,c \rangle.$ The number $b$ is the little orange number and is always positive or $0.$ If you rotate the page, or screen, or your head, so that the arrow appears to point up, then the purple number in the open area on the left is $a,$ while the purple number in the open area on the right is $c.$ Since the numbers $a,c$ are on different sides of the river, one is positive and one negative, so $ac < 0.$ And we always have the same $\Delta = b^2 - 4 a c$ is constant for all forms in the topograph, is positive but not a square. So in these cases, $b < \sqrt \Delta.$
Now, it is very simple to describe those forms at which river crossing occurs. We must have $ac < 0,$
$$ a + c + b > 0 $$ and
$$ a + c - b < 0. $$
Put these together, we get
$$ b > | a + c|. $$
Years ago, I noticed that the forms where river crossing occurs are Lagrange reduced. A discussion of this notion is at webpage and in Duncan A. Buell, Binary Quadratic Forms.
Reduced means, with $\Delta = b^2 - 4 a c > 0,$:
$$ b > 0, \; ac < 0, \; b < \sqrt \Delta, \; \sqrt \Delta - b < 2 |a| < \sqrt \Delta + b, \; \sqrt \Delta - b < 2 |c| < \sqrt \Delta + b. $$
I should emphasize that the two final conditions, for $2 |a|$ or for $2|c|,$ are readily shown to be equivalent in the presence of the other conditions. This is Proposition 3.1 on pages 21-22 of Buell. Also items 1,2,3 after "Then the following are equivalent" on the webpage.
THEOREM: if $\langle a,b,c \rangle$ is reduced, then river crossing occurs at that form.
PROOF:
$$ (|a| + |c|)^2 = a^2 + 2 |ac| + c^2 = a^2 - 2 a c + c^2 = (a-c)^2 $$
$$ \Delta - (|a| + |c|)^2 = b^2 - 4 a c - a^2 + 2 a c - c^2 = b^2 - a^2 - 2 a c - c^2 = b^2 - (a+c)^2. $$
So $$\sqrt \Delta \leq |a| + |c| \; \; \Longleftrightarrow \; \; b \leq |a+c|. $$
From the definition of reduced, square the inequality with $2 |a|$ in the middle,
$$ \Delta - 2 b \sqrt \Delta + b^2 < 4 a^2 < \Delta + 2 b \sqrt \Delta + b^2. $$
Do the same with $2|c|$ but then negate,
$$ -\Delta - 2 b \sqrt \Delta - b^2 < -4 c^2 < -\Delta + 2 b \sqrt \Delta - b^2. $$
Add and divide by 4,
$$ - b \sqrt \Delta < a^2- c^2 < b \sqrt \Delta, $$ or
$$ |a^2 - c^2| < b \sqrt \Delta. $$
Note $$ ||a| - |c|| = ||c| - |a|| = |a+c| $$ because $ac < 0.$ So
$$ ( |a| + |c|) |a+c| < b \sqrt \Delta. $$
If we assume that $b \leq |a+c|$ then $\sqrt \Delta \leq |a| + |c|, $ from which follows
$$ b \sqrt \Delta \leq |a^2 - c^2|, $$ which is a contradiction. So, actually, $b > |a+c|$ and river crossing occurs at this form.
$$ \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc $$
THEOREM: if river crossing occurs at $\langle a,b,c \rangle,$ then the form is reduced.
PROOF:
We have $ac < 0$ and $b > |a + c.|$
This is a calculus type approach, so, like the first theorem, it applies to real numbers.
Define
$$ \beta = |a+c|, \; \; \delta = \beta^2 - 4 a c. $$
So
$$ \delta = a^2 + 2 a c + c^2 - 4 a c = (a-c)^2, $$ and
$$ \sqrt \delta = |a| + |c|. $$
Case (I) $ |a| \geq |c|. $ Then
$$ |a| - |c| = |a+c| = \beta. $$
Then
$$ \sqrt \delta + \beta = 2 |a| $$ and
$$ \sqrt \delta - \beta = 2 |c| \leq 2|a|. $$ Or
$$ \sqrt \delta - \beta \leq 2|a| = \sqrt \delta + \beta . $$
Case (II) $ |a| < |c|. $ Then
$$ |c| - |a| = |a+c| = \beta. $$
Then
$$ \sqrt \delta + \beta = 2 |c| $$ and
$$ \sqrt \delta - \beta = 2 |a| < 2|c|. $$ Or
$$ \sqrt \delta - \beta < 2|c| = \sqrt \delta + \beta . $$
In either case, take real $t = b - \beta > 0$ so that
$$ b = \beta + t > \beta. $$
Here is the calculus type part. $b$ increases, strictly, with $t.$ So $b^2$ increases, strictly, with $t.$ Then $\Delta = b^2 - 4 a c $ increases, strictly, with $t.$ And $\sqrt \Delta$ strictly increases with $t.$ Finally $\sqrt \Delta + b$ strictly increases with $t.$
Now, all along we are keeping $a,c$ and $-4ac$ constant. And from
$$ \Delta - b^2 = (\sqrt \Delta + b)(\sqrt \Delta - b) = - 4 a c $$
we find that
$$ (\sqrt \Delta - b) = \frac{-4ac}{\sqrt \Delta + b} $$
is strictly decreasing with $t.$
As a result, with $t > 0,$ in case (I) above, we find
$$ \sqrt \Delta - b < 2 |a| < \sqrt \Delta + b $$
so the form is reduced.
in case (II) above, we find
$$ \sqrt \Delta - b < 2 |c| < \sqrt \Delta + b $$
so the form is reduced.
$$ \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc \bigcirc $$
For convenience, here is Buell's Proposition 3.1. Suppose $b > 0,\; \; ac < 0,$ and
$$ \sqrt \Delta - b < 2 |a| < \sqrt \Delta + b. $$ Then
$$ \Delta - b^2 = (\sqrt \Delta + b)(\sqrt \Delta - b) = - 4 a c = (2|a|) \cdot (2|c|). $$
Taking $$p =\sqrt \Delta - b, \; \; q =\sqrt \Delta + b, \; \; r = 2 |a|, \; \; s = 2|c| $$
we have four positive terms with
$$ p < r < q, \; \; \; pq = rs. $$ So also $ p < s < q.$